Как эффективно рассчитать среднее "направление" пикселей на изображении в градациях серого?
Итак, я понял, что могу преобразовать изображение в оттенки серого следующим образом:
public static Bitmap GrayScale(this Image img)
{
var bmp = new Bitmap(img.Width, img.Height);
using(var g = Graphics.FromImage(bmp))
{
var colorMatrix = new ColorMatrix(
new[]
{
new[] {.30f, .30f, .30f, 0, 0},
new[] {.59f, .59f, .59f, 0, 0},
new[] {.11f, .11f, .11f, 0, 0},
new[] {0, 0, 0, 1.0f, 0},
new[] {0, 0, 0, 0, 1.0f}
});
using(var attrs = new ImageAttributes())
{
attrs.SetColorMatrix(colorMatrix);
g.DrawImage(img, new Rectangle(0, 0, img.Width, img.Height),
0, 0, img.Width, img.Height, GraphicsUnit.Pixel, attrs);
}
}
return bmp;
}
Теперь я хочу вычислить среднее "направление" пикселей.
Под этим я подразумеваю то, что я хочу рассмотреть, скажем, область 3х3, а затем, если левая сторона темнее правой, то направление будет направо, если нижняя часть темнее верхней, то направление будет вверх, если нижний левый темнее, чем верхний правый, то направление будет верхнее правое. (Подумайте о маленьких векторных стрелках в каждой области 3х3). Возможно, лучшим примером является то, что вы рисуете градиент градаций серого в фотошопе и хотите вычислить, под каким углом они его нарисовали.
Я делал такие вещи, как этот MatLab, но это было много лет назад. Я полагаю, я мог бы использовать матрицу, аналогичную ColorMatrix чтобы вычислить это, но я не совсем уверен, как. Похоже, что эта функция может быть тем, что я хочу; Могу ли я преобразовать его в оттенки серого (как указано выше), а затем сделать что-то с матрицей оттенков серого, чтобы вычислить эти направления?
IIRC, то, что я хочу, очень похоже на обнаружение краев.
После того, как я вычислю эти векторы направления, я просто собираюсь зациклить их и вычислить среднее направление изображения.
Конечная цель - я хочу повернуть изображения так, чтобы их среднее направление всегда было вверх; таким образом, если у меня есть два идентичных изображения, за исключением одного повернутого (90,180 или 270 градусов), они будут в конечном итоге ориентированы одинаково (меня не волнует, если человек окажется вверх ногами).
* snip * Удаление спама. Вы можете просмотреть ревизии, которые вы хотите прочитать остальные мои попытки.
4 ответа
Вычисление среднего значения углов обычно плохая идея:
...
sum += Math.Atan2(yi, xi);
}
}
double avg = sum / (img.Width * img.Height);
Среднее значение набора углов не имеет четкого значения: например, среднее значение одного угла, направленного вверх, и одного угла, направленного вниз, является углом, указывающим направо. Это то, что вы хотите? Предполагая, что "вверх" равно +PI, тогда среднее значение между двумя углами, почти направленными вверх, будет углом, указывающим вниз, если один угол равен PI-[какое-то небольшое значение], другой -PI+[какое-то небольшое значение]. Это, вероятно, не то, что вы хотите. Кроме того, вы полностью игнорируете силу края - большинство пикселей в ваших реальных изображениях вообще не являются краями, поэтому направление градиента в основном шумовое.
Если вы хотите вычислить что-то вроде "среднего направления", вам нужно сложить векторы вместо углов, а затем вычислить Atan2 после цикла. Проблема в том, что эта векторная сумма ничего не говорит об объектах внутри изображения, поскольку градиенты, указывающие в противоположных направлениях, компенсируют друг друга. Это только говорит вам о разнице в яркости между первым / последним рядом и первым / последним столбцом изображения. Это, вероятно, не то, что вы хотите.
Я думаю, что самый простой способ ориентировать изображения - это создать гистограмму угла: создать массив с (например) 360 бинами для 360° направлений градиента. Затем рассчитайте угол и величину градиента для каждого пикселя. Добавьте каждую величину градиента в правый угол. Это даст не один угол, а угловую гистограмму, которую затем можно использовать для ориентации двух изображений друг к другу с помощью простой циклической корреляции.
Вот проверка концепции Mathematica, которую я собрал вместе, чтобы посмотреть, сработает ли она:
angleHistogram[src_] :=
(
Lx = GaussianFilter[ImageData[src], 2, {0, 1}];
Ly = GaussianFilter[ImageData[src], 2, {1, 0}];
angleAndOrientation =
MapThread[{Round[ArcTan[#1, #2]*180/\[Pi]],
Sqrt[#1^2 + #2^2]} &, {Lx, Ly}, 2];
angleAndOrientationFlat = Flatten[angleAndOrientation, 1];
bins = BinLists[angleAndOrientationFlat , 1, 5];
histogram =
Total /@ Flatten[bins[[All, All, All, 2]], {{1}, {2, 3}}];
maxIndex = Position[histogram, Max[histogram]][[1, 1]];
Labeled[
Show[
ListLinePlot[histogram, PlotRange -> All],
Graphics[{Red, Point[{maxIndex, histogram[[maxIndex]]}]}]
], "Maximum at " <> ToString[maxIndex] <> "\[Degree]"]
)
Результаты с образцами изображений:
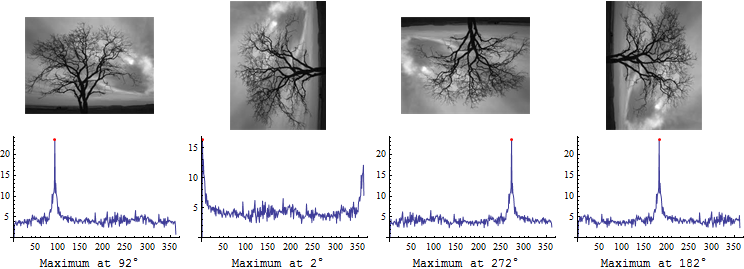
Гистограммы углов также показывают, почему средний угол не может работать: гистограмма, по сути, представляет собой один острый пик, остальные углы примерно одинаковы. Среднее значение этой гистограммы всегда будет зависеть от равномерного "фонового шума". Вот почему у вас есть почти одинаковый угол (около 180°) для каждого из "реальных живых" изображений с вашим текущим алгоритмом.
Изображение дерева имеет один доминирующий угол (горизонт), поэтому в этом случае вы можете использовать режим гистограммы (наиболее частый угол). Но это не будет работать для каждого изображения:
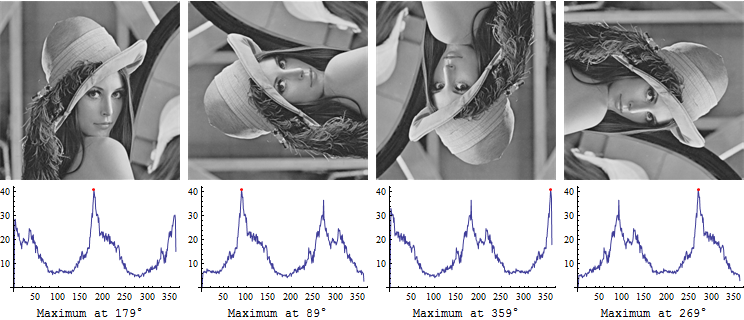
Здесь у вас есть две вершины. Циклическая корреляция должна все еще ориентировать два изображения друг к другу, но простого использования режима, вероятно, недостаточно.
Также обратите внимание, что пик на гистограмме угла не "вверх": на изображении дерева выше, пик на гистограмме угла, вероятно, горизонт. Так что это направлено вверх. На изображении Лены это вертикальная белая полоса на заднем плане, поэтому она направлена вправо. Простая ориентация изображений с использованием наиболее частого угла не приведет к повороту каждого изображения правой стороной вверх.
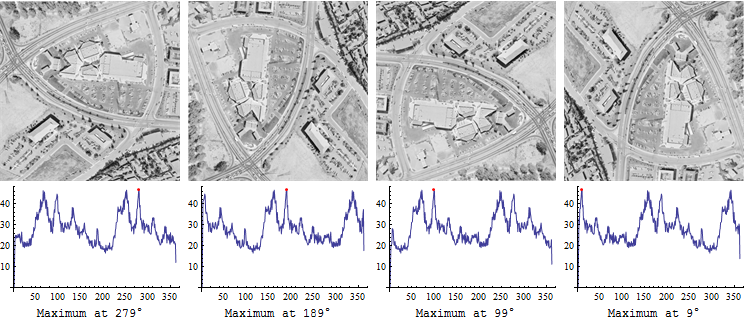
Это изображение имеет еще больше пиков: использование режима (или, возможно, любого отдельного угла) будет ненадежным для ориентации этого изображения. Но угловая гистограмма в целом все же должна дать вам надежную ориентацию.
Примечание: я не обрабатывал изображения заранее, я не пробовал операторы градиента в разных масштабах, я не обрабатывал полученную гистограмму. В реальном приложении вы бы настроили все это, чтобы получить наилучший алгоритм для большого набора тестовых изображений. Это просто быстрый тест, чтобы увидеть, может ли идея работать вообще.
Добавить: Чтобы ориентировать два изображения с помощью этой гистограммы, вы бы
- Нормализуйте все гистограммы, чтобы область под гистограммой была одинаковой для каждого изображения (даже если некоторые из них ярче, темнее или размытее)
- Возьмите гистограммы изображений и сравните их для каждого интересующего вас поворота:
Например, в C#:
for (int rotationAngle = 0; rotationAngle < 360; rotationAngle++)
{
int difference = 0;
for (int i = 0; i < 360; i++)
difference += Math.Abs(histogram1[i] - histogram2[(i+rotationAngle) % 360]);
if (difference < bestDifferenceSoFar)
{
bestDifferenceSoFar = difference;
foundRotation = rotationAngle;
}
}
(Вы можете ускорить это, используя FFT, если длина вашей гистограммы равна степени двух. Но код будет намного сложнее, и для 256 бинов это может не иметь большого значения)
Ну, я могу дать вам другой способ сделать это. Хотя не будет красиво, но надеюсь, что это работает для вас.
Скорее всего, ваши вычисления в порядке. Просто среднее значение градиента в конечном итоге будет отличаться от среднего значения, отличного от ожидаемого. Поэтому я подозреваю, что, глядя на изображение, вы чувствуете, что в нем должен быть другой средний угол. Следовательно;
- Преобразовать изображение в двоичный файл.
- Найти линии, используя грубое преобразование
- Возьмите самую длинную линию и вычислите ее угол. Это должно дать вам угол, который является наиболее заметным.
- Вам может потребоваться некоторая предварительная / постобработка, чтобы получить правильные строки.
И еще один подход. Попробуйте GIST Это в основном реализация, наиболее широко используемая в распознавании сцен. Я считаю, что ваши изображения - реальные сцены, и поэтому я бы предложил использовать этот подход. Этот метод даст вам вектор, который вы сравниваете с различными векторами ориентации одного и того же изображения. Это очень хорошо известная техника, и она обязательно должна применяться в вашем случае.
Подумайте об использовании градиента вашего изображения для вычисления желаемого направления: http://en.wikipedia.org/wiki/Image_gradient
Вам необходимо свернуть изображение с двумя ядрами гауссовой производной (одно в X и одно в Y). Это на самом деле Lx и Ly в ответе выше.
Заранее вычтите среднюю интенсивность пикселей перед вычислением суммированного произведения между скользящим окном (подизображением вашего исходного изображения) и производными Гаусса первого порядка.
Смотрите, например, этот учебник: http://bmia.bmt.tue.nl/people/bromeny/MICCAI2008/Materials/05%20Gaussian%20derivatives%20MMA6.pdf
Выберите оптимальный коэффициент сглаживания сигма>= 1.
Чтобы вычислить ядра Гаусса, дифференцируйте один раз 2D-гауссову функцию (известную из нормального распределения) с 1d-переменной '(x-0)^2', замененной на (x^2 + y^2). Вы можете нарисовать его в 2D, например, в MS Excel.
Удачи!
Майкл