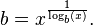Приблизительное число Эйлера в сценарии

Question

Так что это вопрос, который я изменил:

Answer 1

Во-первых, я бы переписал вашу функцию для поиска факториала для более простого

function n = factorial(n)
    n = prod(1:n);
end

Цикл в вашем вопросе не нужен, так как вы никогда не используете переменную цикла i, Я бы не использовал эту функцию для своего решения, так как она может быть довольно медленной, потому что вы должны вычислять избыточную информацию на каждой итерации цикла.

Если вы все еще хотите использовать for цикл вам нужно переписать

function f = factorial(n)
    f = 1; % 0 factorial
    for i = 1:n
        f = f * i;
    end
end

---

Вы можете использовать натуральный логарифм и правила logs, чтобы определить очень точное значение e с которым вы можете сравнить. Значение e вы можете проверить это дано x^(1 / log(x)) где x может быть любым положительным действительным числом, кроме 1, лайк 2, Мы можем видеть это в

Теперь, как мы проверяем, что мы вычислили значение e до 10 знаков после запятой. Хорошо, учитывая, что b сверху очень точное представление e мы можем сравнить с ним, чтобы определить, когда мы достигли точного решения

x = 2; % Any positive number other than 1
c = x^(1 / log(x));
...
if (abs(e - c) < 1e-10)
    break;
end

В моем решении e это приблизительное значение, которое я вычислил с бесконечной суммой. Примечание: абсолютное значение берется для предотвращения ложных срабатываний, когда e - c это отрицательное число.

---

Теперь эффективный метод для вычисления бесконечной суммы. Мы можем использовать способ вычисления факториала, чтобы не вычислять его во время каждой итерации, что значительно повышает эффективность. Во-первых, нам нужна переменная суммы, e в моем случае, чтобы отслеживать наше приблизительное решение. Затем нам нужна другая переменная, чтобы отслеживать факториал, f в моем случае. Как 0 это забавный случай, мы начнем с него

e = 0;
f = 1; % 0 factorial

e = e + 1 / f;

и теперь у нас есть первый элемент в нашей бесконечной сумме. Далее мы можем использовать бесконечную сумму, чтобы вычислить более точное приближение к e, Факториал может обновляться во время каждой итерации с помощью f = f * n; ведущий к

for n = 1:inf
    f = f * n; % Compute new factorial
    e = e + 1 / f; % Infinite sum
    ...
end

Теперь положить, что в целом производит

x = 2; % Any positive number other than 1
c = x^(1 / log(x));

e = 0;
f = 1; % 0 factorial

e = e + 1 / f;

for n = 1:inf
    f = f * n; % Compute new factorial
    e = e + 1 / f; % Infinite sum
    if (abs(e - c) < 1e-10)
        break;
    end
end