Сильно связанные компоненты: алгоритм Косараю

Question

В алгоритме Косараю я натолкнулся на две возможные реализации:

1) Поиск сильно связных компонент в обращенном графе в топологическом порядке вершин исходного графа.

2) Поиск сильно связных компонент в исходном графе в топологическом порядке вершин в обращенном графе.

Я хотел, чтобы было неправильно искать сильно связанные компоненты в исходном графе, используя вершины в обратном топологическом порядке. Это будет лучше с точки зрения памяти, так как нет необходимости в новом списке смежности.

источники:1) E-Maxx, 2) книга CLRS

Answer 1

Вопросы терминологии:

Вы говорите о топологическом порядке, но топологический порядок существует тогда и только тогда, когда граф является DAG (направленным ациклическим). Если вы хотите работать только с группами доступности баз данных, у вас уже есть SCC (сильно связанные компоненты), поскольку каждая вершина является компонентом для себя. Если вы хотите найти SCC на ориентированных графах, вам нужно изменить топологический порядок на время окончания DFS. Книга CLRS упоминает только время окончания f[u]:

3. Вызовите DFS(G^T), но в главном цикле DFS рассмотрите вершины в порядке убывания f[u]...

Переформулировка вашего вопроса:

Неправильно ли искать сильно связанные компоненты в исходном графе с учетом вершин в порядке увеличения времени окончания f[u]?

Ответ:

Да, это неправильно.

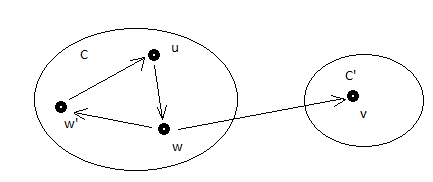
Контрпример: рассмотрим следующий график:

который содержит два компонента C а также C', Если вы запускаете первый DFS (начиная с узла u) вы закончите с одним из двух следующих списков в порядке возрастания к концу времени:

DFS список 1: {v,w',w,u}

DFS список 2: {w',v,w,u}

На самом деле вы спрашиваете, можете ли вы обрабатывать эти списки с самого начала на исходном графике. Если вы выберете первый список, вы извлечете компонент C' через поиск DFS, начиная с узла v, а затем компонент C через поиск DFS, начиная с узла w', Но если вы выберете второй список и запустите DFS с узла w' на исходном графике вы получите только один компонент (весь график), что неверно.

Обратите внимание, что алгоритм Косараю работает в обоих случаях, так как он начинается с конца списка (узел u в обоих случаях) и компонент извлечения C через DFS поиск по перевернутому графику. Составная часть C' будет извлечен позже, когда мы достигнем узла v в списке.

Answer 2

Алгоритм Косараджу — это алгоритм с линейным временем для поиска компонента сильной связности, который будет работать как для ориентированных, так и для неориентированных графов. Чтобы упростить задачу, мы можем сказать на графике, что любая группа узлов, составляющих цикл, является сильно связанным компонентом (SCC). Если мы говорим о подходе Brute force для решения этой проблемы, мы можем выполнить следующие шаги:

1. Найдите все пары кратчайших путей, используя алгоритм Флойда-Уоршелла .
2. Проверьте, если между любыми двумя парами расстояние равно бесконечности, то есть недостижимо, тогда это не SCC , иначе это SCC.

Если говорить о сложности этого подхода, то это займет кубическое время, т.е. O(v^3) . Таким образом, мы можем оптимизировать этот подход, используя алгоритм Косараджу, который может выполнять наш алгоритм за время O(n+m) . Шаги для решения проблемы сильно связанных компонентов с использованием алгоритма Косараджу :

1. Выполните поиск в глубину (DFS) на графе и поместите узлы в стек.
2. Найдите транспонирование графа, перевернув ребра графа.
3. Извлекайте узлы один за другим из стека и снова выполняйте поиск в глубину на модифицированном графе.

Каждая успешная DFS будет состоять из пяти компонентов с сильной связью 1-SCC. Вот как алгоритм Косараджу работает за время O(n+m) , где n — количество узлов в графе, а m — количество ребер.

Answer 3

Я попробовал реализовать ваш алгоритм и протестировал его на одной из платформ кодирования (кодирование ниндзя). По-видимому, в следующем тестовом примере это не удалось.

      int v = 9;
int[][] grid = {
            {0,3},
            {1,7},
            {2,5},
            {3,6},
            {4,1},
            {5,8},
            {6,0},
            {7,4},
            {7,5},
            {8,6},
            {8,2}
    };

Согласно алгоритму Косараджуса, ожидаемое количество связных компонентов равно 3, но результат равен 2. Следовательно, ваше решение неверно.