Энтропия Шеннона для не равновероятного появления символов в блоке

Question

Я пытаюсь понять концепцию энтропии Шеннона и определить длину кода. В первом случае b это массив из 5 символов. Как правило, может быть любое целое число от 1 до 8 в b, Для этого энтропия Шеннеона = NaN.

clear all
b = [1,3,2,6,1];
p_1 = sum(b==1)/length(b);
p_2 = sum(b==2)/length(b);
p_3 = sum(b==3)/length(b);
p_4 = sum(b==4)/length(b);
p_5 = sum(b==5)/length(b);
p_6 = sum(b==6)/length(b);
p_7 = sum(b==7)/length(b);
p_8 = sum(b==8)/length(b);

ShEntropy =  -p_1 * log2(p_1) - (p_2) * log2(p_2) - p_3 * log2(p_3) -p_4 * log2(p_4) -p_5 * log2(p_5) -p_6 * log2(p_6)...
    -p_7 * log2(p_7) -p_8 * log2(p_8)
%codelength
L = max(- log2(p_1), -log2(p_2), -log2(p_3), -log2(p_4), -log2(p_5), -log2(p_6), -log2(p_7), -log2(p_8))

ОБНОВИТЬ:

Прилагается скриншот графика, который позволяет определить длину слова L для коррелированной последовательности, сгенерированной из стационарного эргодического источника. ( http://pubmedcentralcanada.ca/pmcc/articles/PMC4736934/bin/rsos150527supp1.pdf), где они показали расчет длины слова. На графике, поскольку максимальная энтропия достигается при L=8, длина слова равна 8.

** Вопрос **: Формула в уравнении (2) - это коэффициент энтропии Шеннона, который отличается от обычной формулы для источников ИИД. Я не могу понять что было бы N_2L в числителе? В исходном массиве вопросов (до обновления) b имеет длину N =5, Итак, значение энтропии - это скаляр. Но в уравнении (2) я не могу понять, как реализовать это, потому что энтропия Шеннона в этой статье основана на $N$ и 2L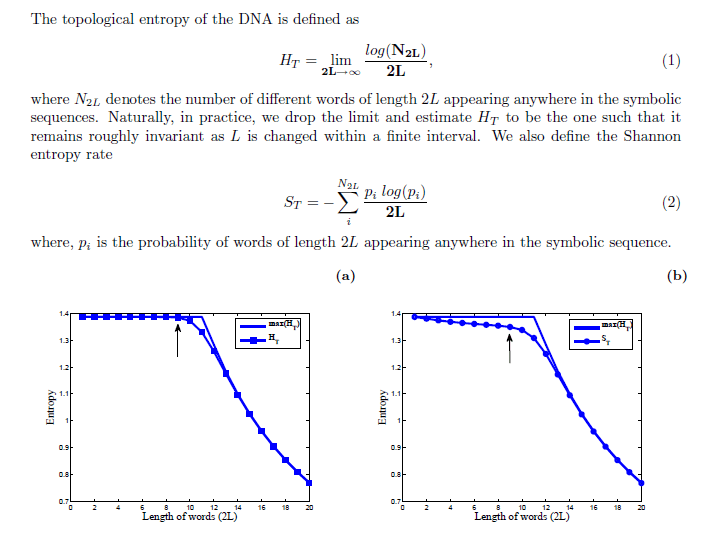

Для любой последовательности, состоящей из уникальных символов k (для моего случая k=8), как реализовать уравнение (2)? Я понимаю, что если length(b) = N Например. N = 20Затем я вычисляю уравнение (2) как S_T для L = 1, S_T для L=2 и так до S_T для N=20, Однако моя путаница возникает из-за того, что энтропия рассчитывается на основе количества уникальных символов, которое в случае двоичного k=2,

Answer 1

Что вы делаете неправильно, так это то, что предел p->0 для p log(p) равен 0. Следовательно, вы можете вычислить его как p*log(p) только для p>0. Для p=0 это будет 0*inf, то есть NaN, но это должно быть ноль.

Нечто подобное поможет:

entropy = @(p) -sum( p(p>0) .* log2(p(p>0)) );

Надеюсь, это поможет.

изменить: в попытке добавить пояснения в ответ на ваши комментарии: приведенная выше формула вычисляет энтропию источника, который излучает N символы, скажем, s1, ..., sN там вероятность увидеть n-й символ sn равна pn.

Если у вас есть источник, который излучает двоичный файл, то у вас есть только два символа, скажем, -1 и +1, с вероятностью p и 1-p, и энтропия этого источника равна -p*log(p) - (1-p)*log(1-p), Конец истории.

Однако это только энтропия источника, если мы будем рассматривать каждый символ отдельно. Может быть, так, что источник испускает кодовые слова, которые состоят из ряда смежных символов, и истинная структура источника раскрывается только после того, как мы посмотрим на последовательность, скажем, L символы, составляющие кодовые слова. Например, на естественном языке, если бы вы смотрели на текст только как на появление букв, вы бы увидели небольшую структуру (e будет более частой, чем, скажем, x, но это почти так), истинная природа структуры в язык становится доступным только после того, как вы смотрите на последовательность символов вместе, например, за sc, вероятно, следует h, или даже более длинные структуры, такие как слова и последовательности слов.

Чтобы отразить это, мы можем взглянуть на энтропию кодовых слов, образованных L последовательные символы. Если ваш источник бинарный, есть N=2^L возможные слова длины L (например, для L=2 Есть четыре кодовых слова (00, 01, 10, 11), для L=3 их восемь и так далее). Каждое слово может быть связано с вероятностью, и энтропия рассчитывается таким же образом, HL = -sum(p(p>0).*log2(p(p>0))),

Если у вас нет способа узнать вероятность аналитически, вы можете попытаться получить ее численно, наблюдая за длинной выборкой и подсчитывая, как часто каждый из N=2^L кодовые слова были замечены. Чем дольше L тем сложнее, так как количество кодовых слов растет очень быстро.