Онлайн алгоритм для доказательства стандартного отклонения

Question

Я видел этот алгоритм в ответе на этот вопрос.

Правильно ли рассчитывается стандартное отклонение? Может кто-нибудь объяснить мне, почему это работает математически? Предпочтительно возвращаясь из этой формулы:

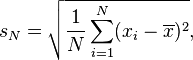
public class Statistics {

    private int n;
    private double sum;
    private double sumsq;

    public void reset() {
        this.n = 0;
        this.sum = 0.0;
        this.sumsq = 0.0;
    }

    public synchronized void addValue(double x) {
        ++this.n;
        this.sum += x;
        this.sumsq += x*x;
    }

    public synchronized double calculateMean() {
        double mean = 0.0;
        if (this.n > 0) {
            mean = this.sum/this.n;
        }
        return mean;
    }

    public synchronized double calculateStandardDeviation() {
        double deviation = 0.0;
        if (this.n > 1) {
            deviation = Math.sqrt((this.sumsq - this.sum*this.sum/this.n)/(this.n-1));
        }
        return deviation;
    }
}

Answer 1

В начале раздела, на который я ссылаюсь, есть доказательство в Википедии.

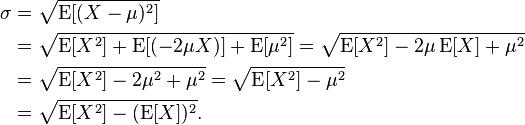
Кстати, я помню откуда-то, что такой способ расчета может привести к большей ошибке. Как вы видете this.sumsq может стать огромным. Принимая во внимание, что вычисление нормальным способом всегда имеет меньшие промежуточные значения

Во всяком случае, я часто использую этот онлайн-расчет, потому что большая часть времени ошибки не имеет большого значения.

Answer 2

Я полагаю, что стандартное отклонение популяции заменит N-1 на N в этой формуле, потому что когда дается среднее значение, на одну степень свободы меньше. Я не статистика, поэтому у меня нет доказательств.

Формула верна - стандартное отклонение - это квадратный корень из среднего отклонения.