Маска усреднения и лапласианская маска при обработке изображений

Question

В данном приложении я применяю усредняющую маску для входных изображений, чтобы уменьшить шум, а затем лапласианскую маску, чтобы улучшить мелкие детали. Кто-нибудь знает, получу ли я такие же результаты, если переверну порядок этих операций в Matlab?

Answer 1

Свертка с ядром Лапласа аналогична использованию информации о производной второй интенсивности об изменениях интенсивности. Так как эта производная чувствительна к шуму, мы часто сглаживаем изображение гауссовым перед применением фильтра Лапласа.

---

Вот пример MATLAB, похожий на тот, что опубликовал @belisarius:

f='http://upload.wikimedia.org/wikipedia/commons/f/f4/Noise_salt_and_pepper.png';
I = imread(f);

kAvg = fspecial('average',[5 5]);
kLap = fspecial('laplacian',0.2);

lapMask = @(I) imsubtract(I,imfilter(I,kLap));

subplot(131), imshow(I)
subplot(132), imshow( imfilter(lapMask(I),kAvg) )
subplot(133), imshow( lapMask(imfilter(I,kAvg)) )

Answer 2

Допустим, у вас есть два фильтра F1 а также F2и изображение I, Если вы пропустите изображение через два фильтра, вы получите ответ, который был определен как

X = ((I * F1) * F2)

Где здесь я использую * представлять свертку.

По ассоциативному правилу свертки это так же, как.

X = (I * (F1 * F2))

используя коммутативность, мы можем сказать, что

X = (I * (F2 * F1)) = ((I * F2) * F1)

Конечно, это в хорошей непрерывной области математики, выполнение этих вещей на машине означает, что будут ошибки округления и некоторые данные могут быть потеряны. Вам также следует подумать о том, являются ли ваши фильтры КИХ, в противном случае вся концепция цифрового фильтра как сверточного типа начинает разрушаться, поскольку ваш фильтр не может действительно вести себя так, как вы этого хотели.

---

РЕДАКТИРОВАТЬ

Дискретная свертка определяется как

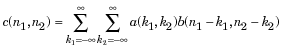
поэтому добавление нулей по краям ваших данных ничего не меняет в математическом смысле.

Как указали некоторые люди, вы получите разные ответы в числовом формате, но это ожидается, когда мы имеем дело с вычислением фактических данных. Эти изменения должны быть небольшими и ограничиваться низкоэнергетическими компонентами выхода свертки (т. Е. Ребрами).

Также важно рассмотреть, как работает операция свертки. Свертка двух наборов данных длины X и длина Y приведет к ответу, который X+Y-1 в длину. В таких программах, как MATLAB и Mathematica, есть некая закулисная магия, дающая вам длинный ответ X или же Y,

Так что в отношении поста @belisarius, похоже, мы действительно говорим то же самое.

Answer 3

Численно результаты не совпадают, но изображения выглядят очень похоже.

Пример в Mathematica:

редактировать

В качестве ответа на комментарий @thron в своем ответе о коммутации линейных фильтров и заполнения, просто рассмотрим следующие операции.

В то время как коммутация фильтра Гаусса и Лапласа без заполнения верна:

list = {1, 3, 5, 7, 5, 3, 1};
gauss[x_] := GaussianFilter[ x, 1]
lapl[x_] := LaplacianFilter[x, 1]
Print[gauss[lapl[list]], lapl[gauss[list]]]
(*
->{5.15139,0.568439,-1.13688,-9.16589,-1.13688,0.568439,5.15139}    
  {5.15139,0.568439,-1.13688,-9.16589,-1.13688,0.568439,5.15139}
*)

Делая то же самое с отступом, вы получите разницу по краям:

gauss[x_] := GaussianFilter[ x, 1, Padding -> 1]
lapl[x_] := LaplacianFilter[x, 1, Padding -> 1]
Print[gauss[lapl[list]], lapl[gauss[list]]]

(*
->{4.68233,0.568439,-1.13688,-9.16589,-1.13688,0.568439,4.68233}
  {4.58295,0.568439,-1.13688,-9.16589,-1.13688,0.568439,4.58295}
*)