Создайте более быструю функцию Фибоначчи для n > 100 в MATLAB / октава
У меня есть функция, которая сообщает мне n-е число в последовательности Фибоначчи. Проблема в том, что он становится очень медленным при попытке найти большие числа в последовательности Фибоначчи, кто-нибудь знает, как я могу это исправить?
function f = rtfib(n)
if (n==1)
f= 1;
elseif (n == 2)
f = 2;
else
f =rtfib(n-1) + rtfib(n-2);
end
Результаты, достижения,
tic; rtfib(20), toc
ans = 10946
Elapsed time is 0.134947 seconds.
tic; rtfib(30), toc
ans = 1346269
Elapsed time is 16.6724 seconds.
Я не могу даже получить значение после 5 минут, делая rtfib(100)
PS: я использую октаву 3.8.1
7 ответов
Если время важно (не методы программирования):
function f = fib(n)
if (n == 1)
f = 1;
elseif (n == 2)
f = 2;
else
fOld = 2;
fOlder = 1;
for i = 3 : n
f = fOld + fOlder;
fOlder = fOld;
fOld = f;
end
end
end
tic;fib(40);toc; ans = 165580141; Elapsed time is 0.000086 seconds.
Вы могли бы даже использовать uint64, n = 92 это максимум, что вы можете получить от uint64:
tic;fib(92);toc; ans = 12200160415121876738; Elapsed time is 0.001409 seconds.
Так как,
fib(93) = 19740274219868223167 > intmax('uint64') = 18446744073709551615
редактировать
Чтобы получить fib(n) вплоть до n = 183, Можно использовать два uint64 как одно число,
со специальной функцией для суммирования,
function [] = fib(n)
fL = uint64(0);
fH = uint64(0);
MaxNum = uint64(1e19);
if (n == 1)
fL = 1;
elseif (n == 2)
fL = 2;
else
fOldH = uint64(0);
fOlderH = uint64(0);
fOldL = uint64(2);
fOlderL = uint64(1);
for i = 3 : n
[fL q] = LongSum (fOldL , fOlderL , MaxNum);
fH = fOldH + fOlderH + q;
fOlderL = fOldL;
fOlderH = fOldH;
fOldL = fL;
fOldH = fH;
end
end
sprintf('%u',fH,fL)
end
LongSum является:
function [s q] = LongSum (a, b, MaxNum)
if a + b >= MaxNum
q = 1;
if a >= MaxNum
s = a - MaxNum;
s = s + b;
elseif b >= MaxNum
s = b - MaxNum;
s = s + a;
else
s = MaxNum - a;
s = b - s;
end
else
q = 0;
s = a + b;
end
Обратите внимание на некоторые осложнения в LongSum может показаться ненужным, но это не так!
(Все дело с внутренним if это то, что я хотел избежать s = a + b - MaxNum в одной команде, потому что он может переполниться и сохранить неактуальное число в s)
Результаты
tic;fib(159);toc; Elapsed time is 0.009631 seconds.
ans = 1226132595394188293000174702095995
tic;fib(183);toc; Прошедшее время составляет 0,009735 секунд.
fib (183) = 127127879743834334146972278486287885163
Тем не менее, вы должны быть осторожны sprintf,
Я также сделал это с тремя uint64, и я мог встать,
tic;fib(274);toc; Истекшее время составляет 0,032249 секунды.
ans = 1324695516964754142521850507284930515811378128425638237225
(Это в значительной степени тот же код, но я мог бы поделиться им, если вам интересно).
Обратите внимание, что у нас есть fib(1) = 1 , fib(2) = 2в соответствии с вопросом, в то время как это чаще встречается fib(1) = 1 , fib(2) = 1 здесь перечислены первые 300 выдумок (спасибо @Rick T).
Похоже, что серия Фибоначчи следует golden ratio о чем подробно говорили here,
Это использовалось в этом коде обмена файлами MATLAB, и я пишу здесь, просто суть этого -
sqrt5 = sqrt(5);
alpha = (1 + sqrt5)/2; %// alpha = 1.618... is the golden ratio
fibs = round( alpha.^n ./ sqrt5 )
Вы можете кормить целое число в n для nth номер в Fibonacci Series или кормить массив 1:n иметь всю серию.
Обратите внимание, что этот метод остается в силе до n = 69 только.
Если у вас есть доступ к набору инструментов Symbolic Math в MATLAB, вы всегда можете просто вызвать функцию Фибоначчи из MuPAD:
>> fib = @(n) evalin(symengine, ['numlib::fibonacci(' num2str(n) ')'])
>> fib(274)
ans =
818706854228831001753880637535093596811413714795418360007
Это довольно быстро:
>> timeit(@() fib(274))
ans =
0.0011
Кроме того, вы можете использовать столько больших чисел, сколько захотите (ограничено только количеством оперативной памяти, которое у вас есть!).
% see if you can beat that!
>> tic
>> x = fib(100000);
>> toc % Elapsed time is 0.004621 seconds.
% result has more than 20 thousand digits!
>> length(char(x)) % 20899
Вот полная стоимость fib(100000): http://pastebin.com/f6KPGKBg
Для достижения больших чисел вы можете использовать символические вычисления. Следующие работы в Matlab R2010b.
syms x y %// declare variables
z = x + y; %// define formula
xval = '0'; %// initiallize x, y values
yval = '1';
for n = 2:300
zval = subs(z, [x y], {xval yval}); %// update z value
disp(['Iteration ' num2str(n) ':'])
disp(zval)
xval = yval; %// shift values
yval = zval;
end
Вы можете сделать это за O(log n) с матричным возведением в степень:
X = [0 1
1 1]
X ^ n даст вам n-е число Фибоначчи в нижнем правом углу; X^n может быть представлен как произведение нескольких матриц X ^ (2 ^ i), поэтому, например, X^11 будет X^1 * X^2 * X^8, i <= log_2(n). И X^8 = (X^4)^2 и т. Д., Не более 2 * log (n) умножений матриц.
Одной из проблем производительности является то, что вы используете рекурсивное решение. Переход к итеративному методу избавит вас от передачи аргументов для каждого вызова функции. Как отметил Оливье, это снизит сложность до линейной.
Вы также можете посмотреть здесь. По-видимому, есть формула, которая вычисляет n-й член последовательности Фибоначчи. Я проверил его до 50-го элемента. Для более высоких значений n это не очень точно.
Реализация быстрого вычисления Фибоначчи в Python может быть следующей. Я знаю, что это Python, а не MATLAB/Octave, однако это может быть полезно.
По сути, вместо того, чтобы снова и снова вызывать одну и ту же функцию Фибоначчи с помощью O (2n), мы сохраняем последовательность Фибоначчи в списке / массиве с помощью O(n):
#!/usr/bin/env python3.5
class Fib:
def __init__(self,n):
self.n=n
self.fibList=[None]*(self.n+1)
self.populateFibList()
def populateFibList(self):
for i in range(len(self.fibList)):
if i==0:
self.fibList[i]=0
if i==1:
self.fibList[i]=1
if i>1:
self.fibList[i]=self.fibList[i-1]+self.fibList[i-2]
def getFib(self):
print('Fibonacci sequence up to ', self.n, ' is:')
for i in range(len(self.fibList)):
print(i, ' : ', self.fibList[i])
return self.fibList[self.n]
def isNonnegativeInt(value):
try:
if int(value)>=0:#throws an exception if non-convertible to int: returns False
return True
else:
return False
except:
return False
n=input('Please enter a non-negative integer: ')
while isNonnegativeInt(n)==False:
n=input('A non-negative integer is needed: ')
n=int(n) # convert string to int
print('We are using ', n, 'based on what you entered')
print('Fibonacci result is ', Fib(n).getFib())
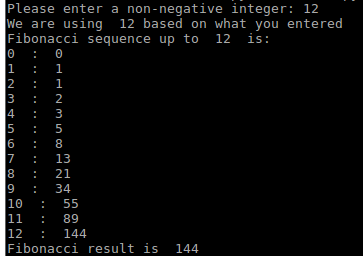
Выход для n=12 было бы как:
Я проверил время выполнения для n=100, 300, 1000 и код действительно быстрый, мне даже не нужно ждать вывода.
Один простой способ ускорить рекурсивную реализацию функции Фибоначчи - это понять, что подстановка f(n-1) по определению,
f(n) = f(n-1) + f(n-2)
= f(n-2) + f(n-3) + f(n-2)
= 2*f(n-2) + f(n-3)
Это простое преобразование значительно сокращает количество шагов, необходимых для вычисления числа в серии.
Если мы начнем с кода OP, слегка исправлено:
function result = fibonacci(n)
switch n
case 0
result = 0;
case 1
result = 1;
case 2
result = 1;
case 3
result = 2;
otherwise
result = fibonacci(n-2) + fibonacci(n-1);
end
И применить наше преобразование:
function result = fibonacci_fast(n)
switch n
case 0
result = 0;
case 1
result = 1;
case 2
result = 1;
case 3
result = 2;
otherwise
result = fibonacci_fast(n-3) + 2*fibonacci_fast(n-2);
end
Затем мы видим 30-кратное улучшение скорости для вычисления 20-го числа в серии (с использованием Octave):
>> tic; for ii=1:100, fibonacci(20); end; toc
Elapsed time is 12.4393 seconds.
>> tic; for ii=1:100, fibonacci_fast(20); end; toc
Elapsed time is 0.448623 seconds.
Конечно , нерекурсивная реализация Рашида еще в 60 раз быстрее: 0,00706792 секунды.