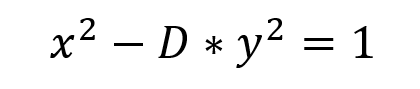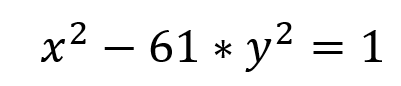Решение уравнения Пелла с непрерывной дробью

Question

Мы знаем, что уравнение Пелла выражается как

который в случае D не является идеальным квадратом, может быть аппроксимирован продолжением дробного расширения D, например, давайте рассмотрим такое уравнение

квадратный корень из 61 может быть аппроксимирован следующим кодом Matlab

>> b=sqrt(61);
>> format rat
>> b

b =

    1523/195  

но у меня есть вопрос: как я могу назначить результат в двух отдельных переменных?

x=1523 
y=195

с этого сайта https://www.quora.com/What-is-the-fast-way-to-solve-the-fundamental-solution-of-Pell-equation

Я понял, что решение основано на числителе и денумераторе. Как я могу назначить дробные части для x и y во время кода в matlab? заранее спасибо

Answer 1

Хотя, по определению, иррациональное число никогда не может быть точно представлено как отношение целых чисел, оно может быть приблизительно представлено с помощью такого отношения в арифметике конечной точности. Это можно сделать через rat функция в различной степени приближения:

>> [n,d] = rat(sqrt(61),1E-4);  (n/d) - sqrt(61)
ans =
   9.5152e-05
>> [n,d] = rat(sqrt(61),1E-8);  (n/d) - sqrt(61)
ans =
  -4.4218e-09
>> [n,d] = rat(sqrt(61),1E-16);  (n/d) - sqrt(61)
ans =
     0

Отмечено, что финал 0 не указывает на истинное равенство терминов; просто равенство в пределах арифметики двойной точности.