Как понять функцию F в логике Бёркса / Уоррена / Райта Лукасевича

Question

Из библиографии главы 1 " Языка программирования 1962 года" я обнаружил это интригующе лаконичное описание логической машины на польском языке (Lukasiewicz). И я думаю, что до этой части логической функции F:

Что означает (2а)? Как это функция?

Вот моя реализация (в PostScript) всего до этой части ( завершенная версия Postscript, C):

%http://www.ams.org/journals/mcom/1954-08-046/

/L{length}def % length of string
/T{ % i D  tail(i) of string
    2 copy L le{ % i<=L(D)
        dup length 2 index sub % i D L(D)-i
        3 2 roll getinterval % D[L-i.*i]
    }{ % i>L(D)
        exch pop % D
    }ifelse
}def
/H{ % i D  head(i) of string
    2 copy L le{ % i<=L(D)
        0 % i D 0
        3 2 roll getinterval % D[0.*i]
    }{
        exch pop % D
    }ifelse
}def

/Wtab 1 dict def
 1 0 1 255{Wtab exch 2 index put}for    pop
 0 (N)    {Wtab exch 2 index put}forall pop
-1 (KA)   {Wtab exch 2 index put}forall pop

/W{ % weight of string or char
    dup type /integertype eq {
        Wtab exch get
    }{
        0 exch { W add } forall
    }ifelse
}def

%Wtab{exch =only( )=only =}forall
%(KAxyz)W =

/D{ % D(d) = 1 - W(d)
    1 exch W sub
}def

/Wmax{ % Wmax(D) = Max(W[T_i(D)]) for i > 0
    [ exch
    0 1 2 index L { % [ ... D i
        1 index T   % [ ... D T(i,D)
        W
        exch        % [ ... W(T(i,D)) D
    } for
    pop % [ ... W(T(i,D))
    counttomark 0 eq { pop 0 }{
        {
            counttomark 1 eq { exch pop exit } if
            2 copy lt { exch } if pop
        }loop
    }ifelse
}def

/Wmin{ % Wmin(D) = Min(W[T_i(D)]) for i > 0
    [ exch
    0 1 2 index L { % [ ... D i
        1 index T   % [ ... D T(i,D)
        W
        exch        % [ ... W(T(i,D)) D
    } for
    pop % [ ... W(T(i,D))
    counttomark 0 eq { pop 0 }{
        {
            counttomark 1 eq { exch pop exit } if
            2 copy gt { exch } if pop
        } loop
    }ifelse
}def

%(KAxyz) Wmax =
%(KAxyz) Wmin =

/PF{ % D is positive formula
    Wmin 0 gt
}def

/WFF{ % D is well-formed formula
    dup PF exch W 1 eq and
}def

/P(01)def
P{
    W 1 ne {ERROR:W_p!=1} if
}forall
/Ptab <<
    P {
        dup
    } forall
>>def

/F{
    dup D 0 gt {
    }{
    }ifelse
}def

Answer 1

Гектометр Хорошо. Я думаю, что начинаю понимать это. P - это алфавит данных, просто 0 а также 1, И игнорируя причудливый способ, которым они его определили, функция степени D из "K" дает 2. Таким образом, это (2a) просто отмечает захват переменной из входной строки, маленькая дельта. Другими словами, входная строка little-delta неявно разбивается на новую little-delta (в данном примере это символ K) и его 2 (степень =2, верно?) аргументов, π_{D (δ)}.. π₁, который определен как этот список, так что он может распространяться на любую арность. Часть εP просто означает, что F должен дать 0 или же 1или, в более общем случае, элемент Р

F сам по себе является параметром для всего этого. Это было прямо наверху. Я забыл

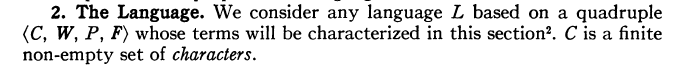
Итак, вот реализация функций K, A, а также N, F контролирует, когда их вызывать, но они должны взламывать свои собственные аргументы из строки.

/P(01)def
P{
    W 1 ne {ERROR:W_p!=1} if
}forall
/Ptab <<
    P { 
        dup
    } forall
>>def

/iP{ % i <- P
    P exch search pop length exch pop exch pop 
}def

/Pi{ % P <- i
    P exch 1 getinterval
}def

/F{
    dup 0 get 
    D 0 gt { % ie. an operator
        dup 0 get % (...) K|A|N 
        exch % K|A|N (...)
        1 1 index length 1 sub getinterval % kan (..)
        exch Ftab exch get exec % F(d,..)
    }{ % leave it alone. F(p)=p
    }ifelse
}def
/Ftab <<
(K)0 get { % crack 2 args from string and convert to indices
    dup 0 1 getinterval iP
    exch 1 1 getinterval iP
    and 
    Pi % convert result back to alphabet P
}
(A)0 get {
    dup 0 1 getinterval iP
    exch 1 1 getinterval iP
    xor 
    Pi  
}
(N)0 get {
    0 1 getinterval iP
    1 add 2 mod 
    Pi  
}
>>def

(K00) F = 
(K01) F =
(K10) F =
(K11) F =

вывод ghostscript:

0
0
0
1

---

Aw. Sheesh. Они полностью говорят то же самое на следующей странице.