Подход минимального диапазона <O (n), O (1)> (от дерева к ограниченному RMQ)

Question

Итак, я прочитал этот учебник TopCoder по RMQ (Range Minimum Query), и у меня возник большой вопрос.

В разделе, где он представил этот подход, я могу понять до сих пор следующее:

(В целом подход использует методологию, представленную в алгоритме Sparse Table (ST), сокращение от LCA до RMQ и от RMQ до LCA)

Учитывая массив A[N], нам нужно преобразовать его в декартово дерево, тем самым превратив проблему RMQ в проблему LCA (самого низкого общего предка). Позже мы можем получить упрощенную версию массива A и сделать ее ограниченной задачей RMQ.

Так что это в основном два преобразования. Так что первая часть RMQ to LCA проста. Используя стек, мы можем выполнить преобразование за O(n) раз, получив массив T[N], где T[i] - родительский элемент элемента i. И дерево завершено.

Но вот что я не могу понять. Подход O(n) нуждается в массиве, где |A[i] - A[i-1]| = 1и этот массив представлен в разделе Сокращение от LCA до RMQ учебного пособия. Это включает в себя Тур Эйлера по этому дереву. Но как это может быть достигнуто с моим конечным результатом преобразования? Мой подход к нему не является линейным, поэтому в этом подходе его следует считать плохим, каким будет линейный подход для этого?

ОБНОВЛЕНИЕ: точка, которая смущает меня

Here's the array A[]:

  n : 0  1  2  3  4  5  6  7  8  9
A[n]: 2  4  3  1  6  7  8  9  1  7

Here's the array T[]:

  n : 0  1  2  3  4  5  6  7  8  9
T[n]: 3  2  0  *  8  4  5  6  3  8  // * denotes -1, which is the root of the tree

//Above is from RMQ to LCA, it's from LCA to RMQ part that confuses me, more below.

Изображение дерева:

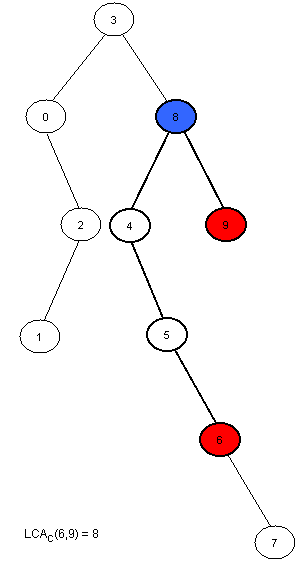
Euler Tour должен знать дочерний узел каждого узла, точно так же как DFS (Поиск в глубину), в то время как у T[n] есть только корень каждого элемента, а не дочерний.

Answer 1

Вот мое текущее понимание того, что вас смущает:

1. Чтобы уменьшить RMQ до LCA, вам нужно преобразовать массив в дерево, а затем выполнить обход Эйлера по этому дереву.
2. Для того, чтобы совершить тур Эйлера, вам нужно хранить дерево таким образом, чтобы каждый узел указывал на своих потомков.
3. Сокращение, которое перечислено от RMQ до LCA, имеет каждый узел, указывающий на его родителя, а не его потомков.

Если это так, то ваши опасения полностью оправданы, но есть простой способ это исправить. В частности, когда у вас есть массив всех родительских указателей, вы можете преобразовать его в дерево, где каждый узел указывает на своих потомков за O(n) раз. Идея заключается в следующем:

• Создайте массив из n узлов. У каждого узла есть поле значения, левый и правый дочерние элементы.
• Сначала установите для n-го узла нулевой левый дочерний элемент, нулевой правый дочерний элемент и значение n-го элемента массива.
• Выполните итерацию по массиву T (где T[n] - родительский индекс n) и выполните следующие действия:
  • Если T[n] = *, то n-я запись является корнем. Вы можете сохранить это для дальнейшего использования.
  • В противном случае, если T[n]
  • В противном случае, если T[n]> n, то вы знаете, что узел n должен быть левым потомком своего родителя, который хранится в позиции T[n]. Поэтому установите левый дочерний узел T[n] -го узла в качестве n-го узла.

Это выполняется за время O(n), поскольку каждый узел обрабатывается ровно один раз.

Как только это будет сделано, вы явно сконструировали нужную древовидную структуру и получите указатель на корень. Оттуда должно быть достаточно просто перейти к остальной части алгоритма.

Надеюсь это поможет!