Как свойство List<T>.Item может быть O(1)? Опечатка?
Я реализую приоритетную очередь и хочу перебрать список, чтобы вставить его в нужное место. В документации говорится, что C# List<T>.Item Свойство O(1):List<T>.Item Имущество
например
int retrivedValue = myIntList[5];
Как это возможно, так как add также является O(1)? Это как съесть печенье и все еще иметь его. Обычные списки в моей голове имеют O(n) для доступа к элементу.
7 ответов
List<T> представляет собой список в представлении, как говорится в документации, он представляет типизированный список объектов, к которым можно получить доступ по индексу. Его элементы могут быть доступны по индексу напрямую и не требуют поэтапного обхода, следовательно, время доступа к элементу составляет O(1). Он реализован внутри как динамический массив, который удваивает свой размер при заполнении (благодаря комментариям!).
Вы можете спутать это с LinkedList<T>, который реализован в виде связанного списка...
Стандартный тип List поддерживается внутренним массивом с O(1) производительностью доступа.
Список не использует реализацию связанного списка.
List<T> поддерживается массивом.
Add Операция - это O (1), амортизируемая по всем добавлениям, что означает, что большинство операций - это O (1), но некоторые - O(N). Всякий раз, когда резервный массив заполняется, он копируется в новый массив двойного размера.
В качестве примера того, как это работает, предположим, что резервный массив начинается с 4 элементов. Первые 4 дополнения - это O (1), но 5-му необходимо скопировать существующие 4 элемента и добавить 5-й, что делает его O(5). Добавление элементов 6, 7 и 8 - это O (1), а добавление элемента 9 - это O(9). Тогда элементы 10-16 также будут O (1).
К тому времени, когда вы добавили 16 элементов в массив, вы выполнили O(28) операций, поэтому добавление N элементов требует почти O(2N) операций. Таким образом, добавление одного элемента в среднем равно O(2) = O(1).
Возможно, вы захотите взглянуть на это, чтобы понять и при этом использовать наиболее подходящую структуру данных.
Ниже приведена сводная таблица:
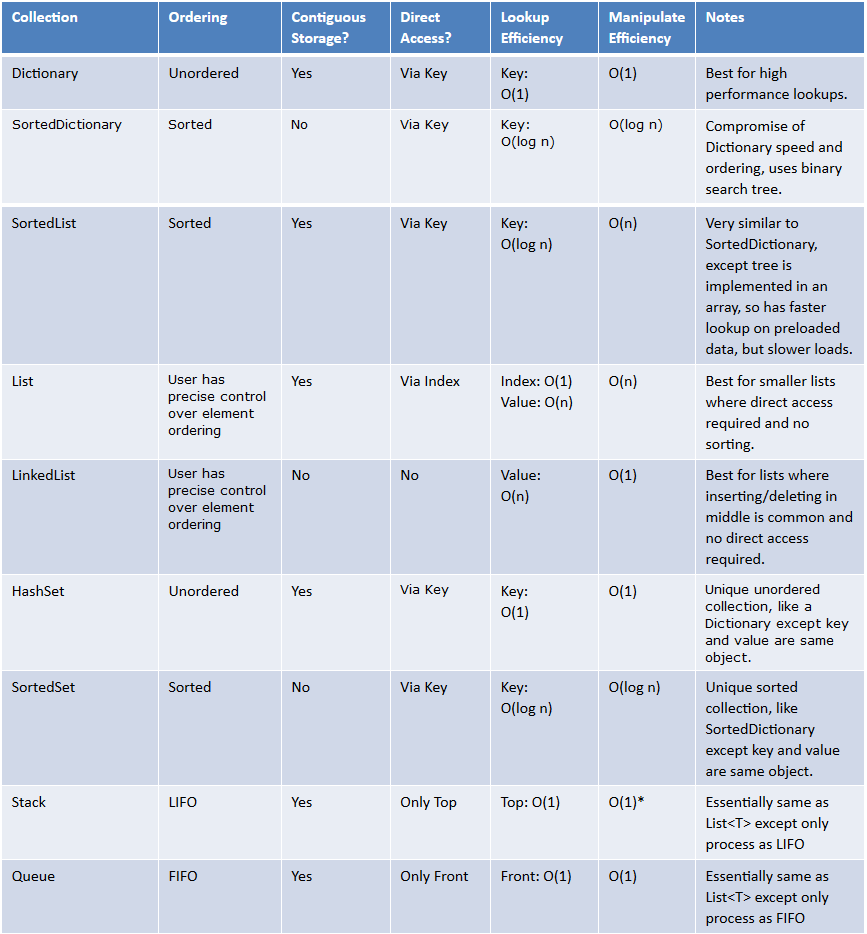
У вас есть только O(n) если вам нужно перебрать список, чтобы получить элемент.
В этом примере вы обращаетесь к внутреннему массиву по индексу, поэтому не нужно повторять.
Несмотря на привлекательную сложность поиска по списку, основанную на элементном индексе, я хотел бы знать, может ли ваши потребности лучше удовлетворяться с помощью SkipList, как описано в Обширном исследовании структур данных с использованием C# 2.0, на который ссылается здесь, поскольку приоритет упорядочения не является уникальным.
Динамическое расширение массива для n вставок (n неограниченно) фактически равно O(n)
Если резервная копия массива дублируется по размеру каждый раз, и n может увеличиваться без ограничений, то число перераспределений массива будет равно O(logn) и в каждой точке будет иметь размер 2^k; k = 1,2,3...
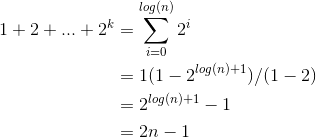
List<T>.Item versus List<T>.Contains
Доступ к элементам в Списке - O(1), если индекс известен, но чтобы сохранить правильный порядок, основанный на приоритете, вам нужно будет либо использовать какой-то внешний механизм упорядочения, либо использовать .Contains, но этот 2-й метод не является O(1).
Скиплисты имеют O(logn) сложность поиска; разрешает очередь PriorityQueue O(logn) и очередь O(1)
Идея состоит в том, что SkipList представляет собой связанный список со случайно вставленными указателями "ускоренной перемотки вперед", чтобы преодолеть сложность O(n) поиска в списке ссылок. Каждый узел имеет высоту K и K следующих указателей. Не вдаваясь в детали, высоты распределяются, и функция next() выбирает соответствующий указатель таким образом, чтобы выполнить поиск O(logn). Однако узел, который необходимо удалить из очереди, всегда будет находиться на одном конце связанного списка.
Онлайн поведение
Память ограничена, и, практически говоря, приоритетная очередь не будет расти вечно. Можно утверждать, что очередь увеличивается до определенного размера, а затем никогда не перераспределяется. Но тогда, это сжимается? Если список становится фрагментированным, операция сжатия звучит даже дороже, чем операция увеличения. Если поддерживается сжатие, то стоимость будет оплачиваться каждый раз, когда список становится слишком маленьким, и затем впоследствии стоимость будет оплачиваться, когда список становится слишком большим. Если это не поддерживается, то память, связанная с наибольшим размером очереди, останется выделенной. Поскольку это приоритетная очередь, на самом деле кажется вероятным, что очередь может увеличиваться по мере поступления в нее работы, а затем уменьшаться (логически) до 0,. Там могут быть редкие обстоятельства, что он будет очень большим, если потребительская сторона отстает.
Список внутренне использует массив, поэтому индексация является прямой операцией. Кроме того, добавить в конце быстро (если не требуется realoc). Вставка и удаление - O(n), хотя, потому что все элементы массива должны быть перемещены. На практике это тоже не так уж плохо, потому что перемещение реализовано как одно перемещение блока правой части массива.