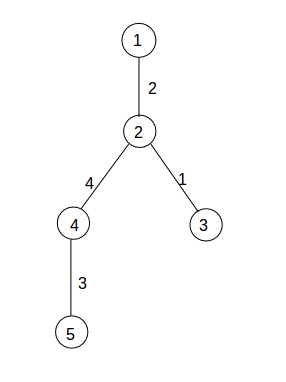
Максимальный вес ребра от одного узла A до узла B

Question

Дан связный неориентированный граф, имеющий N узлов (1 <= N <= 2 * 10 ^ 5) и N-1 ребер. Определим функцию F (a, b), где F (a, b) равен максимальному весу ребра на пути от a до b. Как нам найти сумму F (a, b) для всех a, b таких, что 1 <= a, b <= N (mod 10 ^ 9 + 7)

Пример фигуры

F (a, b) равен максимальному весу ребра на пути от a до b.

F (1, 2) = 2

F (1, 3) = 2

F (1, 4) = 4

F (1, 5) = 4

F (2, 3) = 1

F (2, 4) = 4

F (2,5) = 4

F (3, 4) = 4

F (3, 5) = 4

F (4, 5) = 3

Сумма F по всем парам равна 32.

Answer 1

Для этого мы можем использовать вариант алгоритма MST Крускала (Крускал сортирует ребра, увеличивая вес, жадно вставляя те, которые не делают цикл, с помощью непересекающейся структуры данных набора). Инициализировать текущую сумму до нуля; всякий раз, когда мы объединяем непересекающийся набор размера S1 (эта информация доступна как побочный продукт структуры данных непересекающегося набора, которая объединяет по размеру) с непересекающимся набором размера S2 через ребро веса w, добавьте S1*S2*w к сумма мод 10^9 + 7.