Количество установленных битов в целых числах

Question

Я изучаю различные методы подсчета битов или методы подсчета чисел для заданного целого числа, в течение этих дней я пытался выяснить, как работают следующие алгоритмы

pop(x)=-sum(x<<i)   where i=0:31

я думаю, что после расчета каждого значения х, мы получим

x+2*x+4*x+8*x+16*x+..............+2^31*x  =4294967294*x

если мы умножим это на -1, мы получим -4294967294*x, но как он рассчитывает количество бит? Пожалуйста, помогите мне понять этот метод хорошо. спасибо

Answer 1

Я полагаю, вы имеете в виду

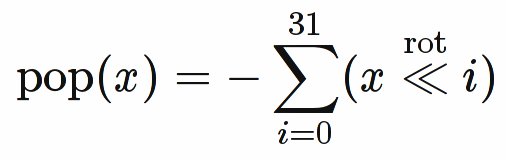
как видно на обложке книги "Восторг хакера", где символ означает вращение влево, а не сдвиг влево, что приведет к неправильным результатам и отрицательным результатам.

Этот метод работает, потому что вращение приведет к тому, что все двоичные цифры x появятся во всех возможных битах во всех терминах, и из-за дополнения до 2.

Возьмите более простой пример. Рассмотрим числа только с 4 двоичными цифрами, где цифры могут быть представлены как ABCD тогда суммирование означает:

  ABCD  // x <<rot 0
+ BCDA  // x <<rot 1
+ CDAB  // x <<rot 2
+ DABC  // x <<rot 3

Мы отмечаем, что в каждом столбце есть все A, B, C, D. Теперь ABCD на самом деле означает "2³ A + 2² B + 2¹ C + 2⁰ D", поэтому суммирование просто:

  2³ A        + 2² B        + 2¹ C        + 2⁰ D
+ 2³ B        + 2² C        + 2¹ D        + 2⁰ A
+ 2³ C        + 2² D        + 2¹ A        + 2⁰ B
+ 2³ D        + 2² A        + 2¹ B        + 2⁰ C
——————————————————————————————————————————————————————
= 2³(A+B+C+D) + 2²(B+C+D+A) + 2¹(C+D+A+B) + 2⁰(D+A+B+C)
= (2³ + 2² + 2¹ + 2⁰) × (A + B + C + D)

(A + B + C + D) - это число населения x, а (2³ + 2² + 2¹ + 2⁰) = 0b1111 равно -1 в дополнении 2, поэтому сумма является отрицательной величиной числа населения.

Аргумент может быть легко расширен до 32-битных чисел.

Answer 2

#include <stdio.h>
#include <conio.h>

unsigned int f (unsigned int a , unsigned int b);

unsigned int f (unsigned int a , unsigned int b)
{
   return a ?   f ( (a&b) << 1, a ^b) : b;
}

int bitcount(int n) {
    int tot = 0;

    int i;
    for (i = 1; i <= n; i = i<<1)
        if (n & i)
            ++tot;

    return tot;
}

int bitcount_sparse_ones(int n) {
    int tot = 0;

    while (n) {
        ++tot;
        n &= n - 1;
    }

    return tot;
}

int main()
{

int a = 12;
int b = 18;

int c = f(a,b);
printf("Sum = %d\n", c);

int  CountA = bitcount(a);
int  CountB = bitcount(b);

int CntA = bitcount_sparse_ones(a);
int CntB = bitcount_sparse_ones(b);

printf("CountA = %d and CountB = %d\n", CountA, CountB);
printf("CntA = %d and CntB = %d\n", CntA, CntB);
getch();

return 0;

}

Answer 3

Использование побитовой операции : это один из наиболее эффективных подходов.

      int countSetBits(int x) { 
    int count = 0; 
    while (x) { 
        x &= (x-1); 
        count++; 
    } 
    return count; 
} 

Это алгоритм Брайана Кернигана . Он канадский ученый-компьютерщик. Мы обсудим алгоритмы на примере ниже -

      Example:
    
      let, x = 6 (110), and initially, count = 0
      now, n = 6 & (6-1)      decimal
             = 110 & 101      binary 
             = 100            decimal
       so, n = 4, count = 1
    again, n = 4 & (4-1)      decimal
             = 100 & 011      binary
             = 0              decimal
       so, n = 0, count = 2
    as, now n is 0, we get count of set bit = 2

Ссылка: Bitwise Hacks!