Как найти основную частоту звука гитарной струны?
Я хочу создать приложение для гитарного тюнера для Iphone. Моя цель - найти основную частоту звука, генерируемого гитарной струной. Я использовал биты кода из образца aurioTouch, предоставленного Apple, для вычисления частотного спектра, и я нахожу частоту с наибольшей амплитудой. Это работает хорошо для чистых звуков (те, которые имеют только одну частоту), но для звуков из гитарной струны это дает неправильные результаты. Я читал, что это из-за обертонов, генерируемых гитарной струной, которые могут иметь более высокие амплитуды, чем основная. Как я могу найти основную частоту, чтобы она работала на гитарных струнах? Есть ли в C/C++/Obj-C библиотека с открытым исходным кодом для анализа звука (или обработки сигналов)?
3 ответа
Вы можете использовать автокорреляцию сигнала, которая является обратным преобразованием квадрата величины ДПФ. Если вы производите выборку с частотой 44100 отсчетов / с, то базовая частота 82,4 Гц составляет около 535 отсчетов, тогда как 1479,98 Гц составляет около 30 отсчетов. Посмотрите на пик положительного лага в этом диапазоне (например, от 28 до 560). Убедитесь, что в вашем окне как минимум два периода самых длинных фундаментальных значений, а здесь будет 1070 отсчетов. До следующей степени два это буфер с 2048 выборками. Для лучшего разрешения по частоте и менее смещенной оценки используйте более длинный буфер, но не настолько длинный, чтобы сигнал больше не был приблизительно стационарным. Вот пример в Python:
from pylab import *
import wave
fs = 44100.0 # sample rate
K = 3 # number of windows
L = 8192 # 1st pass window overlap, 50%
M = 16384 # 1st pass window length
N = 32768 # 1st pass DFT lenth: acyclic correlation
# load a sample of guitar playing an open string 6
# with a fundamental frequency of 82.4 Hz (in theory),
# but this sample is actually at about 81.97 Hz
g = fromstring(wave.open('dist_gtr_6.wav').readframes(-1),
dtype='int16')
g = g / float64(max(abs(g))) # normalize to +/- 1.0
mi = len(g) / 4 # start index
def welch(x, w, L, N):
# Welch's method
M = len(w)
K = (len(x) - L) / (M - L)
Xsq = zeros(N/2+1) # len(N-point rfft) = N/2+1
for k in range(K):
m = k * ( M - L)
xt = w * x[m:m+M]
# use rfft for efficiency (assumes x is real-valued)
Xsq = Xsq + abs(rfft(xt, N)) ** 2
Xsq = Xsq / K
Wsq = abs(rfft(w, N)) ** 2
bias = irfft(Wsq) # for unbiasing Rxx and Sxx
p = dot(x,x) / len(x) # avg power, used as a check
return Xsq, bias, p
# first pass: acyclic autocorrelation
x = g[mi:mi + K*M - (K-1)*L] # len(x) = 32768
w = hamming(M) # hamming[m] = 0.54 - 0.46*cos(2*pi*m/M)
# reduces the side lobes in DFT
Xsq, bias, p = welch(x, w, L, N)
Rxx = irfft(Xsq) # acyclic autocorrelation
Rxx = Rxx / bias # unbias (bias is tapered)
mp = argmax(Rxx[28:561]) + 28 # index of 1st peak in 28 to 560
# 2nd pass: cyclic autocorrelation
N = M = L - (L % mp) # window an integer number of periods
# shortened to ~8192 for stationarity
x = g[mi:mi+K*M] # data for K windows
w = ones(M); L = 0 # rectangular, non-overlaping
Xsq, bias, p = welch(x, w, L, N)
Rxx = irfft(Xsq) # cyclic autocorrelation
Rxx = Rxx / bias # unbias (bias is constant)
mp = argmax(Rxx[28:561]) + 28 # index of 1st peak in 28 to 560
Sxx = Xsq / bias[0]
Sxx[1:-1] = 2 * Sxx[1:-1] # fold the freq axis
Sxx = Sxx / N # normalize S for avg power
n0 = N / mp
np = argmax(Sxx[n0-2:n0+3]) + n0-2 # bin of the nearest peak power
# check
print "\nAverage Power"
print " p:", p
print "Rxx:", Rxx[0] # should equal dot product, p
print "Sxx:", sum(Sxx), '\n' # should equal Rxx[0]
figure().subplots_adjust(hspace=0.5)
subplot2grid((2,1), (0,0))
title('Autocorrelation, R$_{xx}$'); xlabel('Lags')
mr = r_[:3 * mp]
plot(Rxx[mr]); plot(mp, Rxx[mp], 'ro')
xticks(mp/2 * r_[1:6])
grid(); axis('tight'); ylim(1.25*min(Rxx), 1.25*max(Rxx))
subplot2grid((2,1), (1,0))
title('Power Spectral Density, S$_{xx}$'); xlabel('Frequency (Hz)')
fr = r_[:5 * np]; f = fs * fr / N;
vlines(f, 0, Sxx[fr], colors='b', linewidth=2)
xticks((fs * np/N * r_[1:5]).round(3))
grid(); axis('tight'); ylim(0,1.25*max(Sxx[fr]))
show()
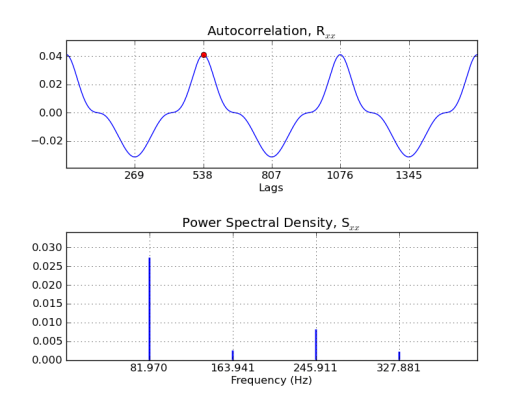
Выход:
Average Power
p: 0.0410611012542
Rxx: 0.0410611012542
Sxx: 0.0410611012542
Пиковая задержка составляет 538, что составляет 44100/538 = 81,97 Гц. Ациклическое ДПФ первого прохода показывает фундамент в бине 61, который составляет 82,10 +/- 0,67 Гц. Во втором проходе используется длина окна 538*15 = 8070, поэтому частоты DFT включают основной период и гармоники струны. Это позволяет использовать универсальную циклическую автокорреляцию для улучшенной оценки PSD с меньшим гармоническим расширением (то есть корреляция может периодически оборачиваться вокруг окна).
Редактировать: Обновлено, чтобы использовать метод Уэлча для оценки автокорреляции. Перекрывающиеся окна компенсируют окно Хемминга. Я также вычисляю конусное смещение окна Хэмминга, чтобы отменить автокорреляцию.
Редактировать: Добавлен 2-й проход с циклической корреляцией для очистки спектральной плотности мощности. Этот проход использует 3 непересекающихся прямоугольных окна длиной 538*15 = 8070 (достаточно коротких, чтобы быть почти неподвижными). Смещение для циклической корреляции является константой, а не коническим смещением окна Хэмминга.
Найти музыкальные высоты в аккорде гораздо сложнее, чем оценить высоту одной струны или ноты, сыгранной одновременно. Обертоны для нескольких нот в аккорде могут перекрываться и чередоваться. И все ноты в общих аккордах могут сами по себе быть на частоте обертона для одной или нескольких несуществующих нот нижнего тона.
Для отдельных нот автокорреляция является распространенной техникой, используемой некоторыми гитарными тюнерами. Но с автокорреляцией, вы должны знать о некоторой потенциальной октавной неопределенности, поскольку гитары могут производить негармоничные и затухающие обертоны, которые, таким образом, не совсем совпадают от периода основного тона к периоду основного тона. Cepstrum и Harmonic Product Spectrum - два других метода оценки основного тона, которые могут иметь или не иметь различные проблемы, в зависимости от гитары и ноты.
RAPT является одним из опубликованных алгоритмов для более надежной оценки основного тона. Инь это другое.
Кроме того, Objective C является расширенным набором ANSI C. Таким образом, вы можете использовать любые подпрограммы C DSP, которые вы найдете для оценки основного тона в приложении Objective C.