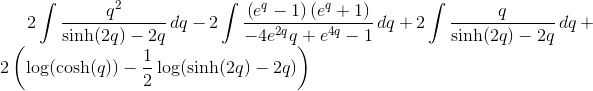Mathematica Integrate возвращает интеграл

Question

Я пытаюсь интегрировать следующую функцию:

(q (1 + q) - E^-q Sinh[q])/(-q + Cosh[q] Sinh[q]) - (
 2 q Tanh[q])/(-q + Cosh[q] Sinh[q])    

Я уже решил это численно, но мне действительно нужен неопределенный интеграл, используемый таким образом:

 In[67]:= Integrate[(
  q (1 + q) - E^-q Sinh[q])/(-q + Cosh[q] Sinh[q]) - (
  2 q Tanh[q])/(-q + Cosh[q] Sinh[q]), q]

но в качестве вывода я снова получаю подынтегральное выражение:

 Out[67]= \[Integral]((
     q (1 + q) - E^-q Sinh[q])/(-q + Cosh[q] Sinh[q]) - (
     2 q Tanh[q])/(-q + Cosh[q] Sinh[q])) \[DifferentialD]q    

какие-либо предложения о том, как правильно выполнить это вычисление? заранее спасибо

Answer 1

Вы можете разложить этот интеграл:

eq = (q (1 + q) - E^-q Sinh[q])/(-q + 
  Cosh[q] Sinh[q]) - (2 q Tanh[q])/(-q + Cosh[q] Sinh[q]);
Integrate[#, q] & /@ Simplify /@ Expand[eq]

Одна часть этого интеграла может быть выполнена, остальные содержат самые простые, но все еще не выраженные в стандартных математических функциях интегралы.

Вы можете делать эти интегралы численно или искать приближенную форму, например, используя разложение в ряд.

Примерное расширение серии вы можете найти по ссылке: wolframalpha.com