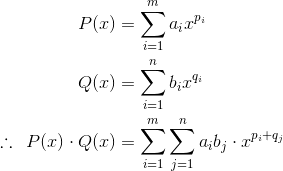Как формально рассчитать время выполнения наивной полиномиальной оценки в точке

Question

Я интуитивно понимаю, почему временная сложность наивной полиномиальной оценки в точке равна ϴ(n^2). Однако я не уверен, как формально рассчитать время выполнения, чтобы показать его.

Заранее спасибо!

Answer 1

Не совсем ϴ(n^2), но ϴ(mn), где m а также n число слагаемых в каждом полиноме.

Есть тривиально m * n требуется умножение, равное количеству способов сопряжения коэффициентов a_i * b_j между двумя полиномами.

Есть также дополнения для рассмотрения; однако, поскольку любая определенная пара коэффициентов a_i, b_j принадлежит только одной степени x, он будет добавлен только один раз к коэффициенту в последнем полиноме. Поэтому может быть только до O(mn) дополнения.

Поэтому общая временная сложность наивного умножения ϴ(mn),