Интерполяция вращения
NB: Я представлю этот вопрос в градусах чисто для простоты, радианы, градусы, различные нулевые значения, проблема, по сути, та же.
У кого-нибудь есть идеи по поводу кода ротационной интерполяции? Имеется функция линейной интерполяции: Lerp(от, до, сумма), где сумма равна 0...1, которая возвращает значение между от и до, по сумме. Как я могу применить эту же функцию к вращательной интерполяции между 0 и 360 градусами? Учитывая, что градусы не должны возвращаться за пределы 0 и 360.
С учетом этого единичного круга для градусов:
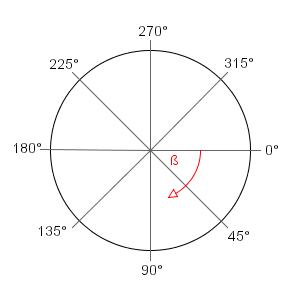
где от = 45 и до = 315 алгоритм должен взять кратчайший путь к углу, то есть он должен пройти через ноль, до 360, а затем до 315 - и не полностью до 90, 180, от 270 до 315.
Есть ли хороший способ добиться этого? Или это будет ужасный беспорядок блоков if()? Я пропускаю какой-то хорошо понятый стандартный способ сделать это? Любая помощь будет оценена.
10 ответов
Я знаю, что это 2 года, но я недавно искал ту же проблему, и я не вижу элегантного решения, если здесь не опубликовано ifs, так что вот так:
shortest_angle=((((end - start) % 360) + 540) % 360) - 180;
return shortest_angle * amount;
вот и все
ps: конечно, % означает по модулю, а shorttest_angle - это переменная, которая содержит весь угол интерполяции
Извините, это было немного запутанно, вот более краткая версия:
public static float LerpDegrees(float start, float end, float amount)
{
float difference = Math.Abs(end - start);
if (difference > 180)
{
// We need to add on to one of the values.
if (end > start)
{
// We'll add it on to start...
start += 360;
}
else
{
// Add it on to end.
end += 360;
}
}
// Interpolate it.
float value = (start + ((end - start) * amount));
// Wrap it..
float rangeZero = 360;
if (value >= 0 && value <= 360)
return value;
return (value % rangeZero);
}
Кто-нибудь получил более оптимизированную версию?
Я думаю, что лучший подход - это интерполировать грех и соз, потому что они не страдают от многократного определения формы. Пусть w = "количество", так что w = 0 - это угол A, а w = 1 - это угол B. Тогда
CS = (1-w)*cos(A) + w*cos(B);
SN = (1-w)*sin(A) + w*sin(B);
C = atan2(SN,CS);
Нужно конвертировать в радианы и градусы по мере необходимости. Также нужно настроить ветку. Для atan2 C возвращается в диапазоне от -pi до pi. Если вы хотите от 0 до 2pi, просто добавьте пи к C.
NB: с использованием кода C#
После некоторого безумного рытья в моем мозгу, вот что я придумала. По сути, посылка должна выполнить обтекание 0-360 в последнюю минуту. Внутренне обработайте значения за пределами 0-360, а затем оберните их внутри 0-360 в точке, где значение запрашивается у функции.
В точке, где вы выбираете начало и конец, вы выполняете следующее:
float difference = Math.Abs(end - start);
if (difference > 180)
{
// We need to add on to one of the values.
if (end > start)
{
// We'll add it on to start...
start += 360;
}
else
{
// Add it on to end.
end += 360;
}
}
Это дает вам фактические начальные и конечные значения, которые могут быть за пределами 0-360...
У нас есть функция обтекания, которая обеспечивает значение от 0 до 360...
public static float Wrap(float value, float lower, float upper)
{
float rangeZero = upper - lower;
if (value >= lower && value <= upper)
return value;
return (value % rangeZero) + lower;
}
Затем в точке вы запрашиваете текущее значение из функции:
return Wrap(Lerp(start, end, amount), 0, 360);
Это почти наверняка не самое оптимальное решение проблемы, однако, похоже, оно работает последовательно. Если у кого-то есть более оптимальный способ сделать это, это было бы здорово.
Я хотел переписать свой ответ, чтобы лучше объяснить ответ на вопрос. Я использую EXCEL для своих формул, и градусы для своих единиц.
Для простоты, B является большим из двух значений, и A является меньшим из двух значений. Ты можешь использовать MAX() а также MIN() соответственно в вашем решении позже.
ЧАСТЬ 1 - КАК ПУТЬ ПОЙТИ?
Сначала мы хотим выяснить, в каком направлении мы хотим выполнить расчет по часовой стрелке или против часовой стрелки. Мы используем IF() Заявление для этого:
IF( (B-A)<=180, (Clockwise_Formula), (AntiClockwise_Formula) )
Приведенная выше формула проверяет, идет ли против часовой стрелки от B в A (что аналогично движению по часовой стрелке от A в B) меньше или равно 180 градусам. Если нет, то будет короче идти в другом направлении.
Чтобы проверить это работает: 90 - 45 = 45 (что меньше или равно 180) делает оператор IF ИСТИННЫМ, поэтому направление по часовой стрелке короче, а 315 - 45 = 270 (что больше 180) делает оператор if ЛОЖЬ, поэтому формула против часовой стрелки будет короче.
ЧАСТЬ 2 - ЧАСОВЫЕ ФОРМУЛЫ
Теперь вы хотите интерполировать N время между A а также Bпо часовой стрелке или против часовой стрелки. Формула по часовой стрелке относительно проста.
Clockwise_Formula: ((B-A)/N*S)+A
куда S является подсчетом числа интерполяций, начиная с 1 и заканчивая N-1 (если S = NВаш ответ будет B)
Пример: A = 90, B = 270, N = 4
S=1: ((270-90)/4*1)+90 = 135
S=2: ((270-90)/4*2)+90 = 180
S=3: ((270-90)/4*3)+90 = 225
ЧАСТЬ 3 - ФОРМУЛА ПРОТИВ ЧАСОВ
Формула против часовой стрелки будет немного сложнее, потому что нам нужно пересечь против часовой стрелки на 360 градусов. Самый простой метод, который я могу придумать, это добавить 360 к A, затем смодулируйте ответ на 360, используя MOD(FORMULA,VALUE) функция.
Вам также придется поменяться A а также B вокруг в формуле, потому что B теперь самое маленькое число. (Это может показаться немного запутанным, но это работает!)
(Unmodulated) AntiClockwise_Formula: (((A+360)-B)/N*S)+B
Пример: A = 60, B = 300, N = 4
S=1: (((60+360)-300)/4*1)+300 = 330
S=2: (((60+360)-300)/4*2)+300 = 360
S=3: (((60+360)-300)/4*3)+300 = 390
ЧАСТЬ 4 - ОГРАНИЧЕНИЕ ОТВЕТОВ НА ОТ 0 И 360
Видите, как иногда (но не всегда) ответы будут больше 360? Это где упаковка вашего Anticlockwise_formula в MOD() функция входит в:
AntiClockwise_Formula: MOD((((A+360)-B)/N*S)+B,360)
Модулирование примера, использованного в части 3, даст вам:
S=1: 330
S=2: 0
S=3: 30
ЧАСТЬ 5 - ВСЕ ВМЕСТЕ
Объединив все элементы из частей 1-4 вместе, ответ:
IF((B-A)<=180,((B-A)/N*S)+A,MOD((((A+360)-B)/N*S)+B,360))
Куда:
A = Меньшее из двух значений (вы можете заменить A на MIN ())
B = Большее из двух значений (вы можете заменить B на MAX ())
N = Количество интерполяций, которые вы хотите сделать (например, 2 - половина, 3 - на трети и т. Д.)
S = Инкриментальный счет до макс. N-1 (объяснение см. В части 2)
Мой предпочтительный способ справиться с углом - использовать единицы, имеющие степень 2 на оборот. Например, если вы используете 16-битные целые числа со знаком для представления от -180 до +180 градусов, вы можете просто взять (from-to)/num_steps, чтобы выполнить интерполяцию. Сложение и вычитание углов всегда работает, поскольку двоичные значения переполняются прямо в точке, где вы переходите от 360 до 0.
Что вы, вероятно, хотите сделать в вашем случае - это математика по модулю 360. Таким образом, разность углов вычисляется как (от-до)%360. Есть еще некоторые проблемы со знаком, которые были рассмотрены в других вопросах SO.
Модификация ответа user151496 (оригинал был в градусах, а также дал мне неправильный результат):
def interp_angle(theta_1, theta_2, ratio):
shortest_angle = ((((theta_2 - theta_1) % (np.pi*2)) + np.pi) % (np.pi*2)) - np.pi
return (theta_1 + shortest_angle * ratio) % (np.pi*2)
Тесты: бег с
theta1, theta2 = 0, 0.5
print('Average of {:.4g}pi rad and {:.4g}pi rad = {:.4g}pi rad'.format(theta1, theta2, interp_angle(theta1*np.pi, theta2*np.pi, 0.5)/np.pi))
theta1, theta2 = 0, 0.99
print('Average of {:.4g}pi rad and {:.4g}pi rad = {:.4g}pi rad'.format(theta1, theta2, interp_angle(theta1*np.pi, theta2*np.pi, 0.5)/np.pi))
theta1, theta2 = 0, 1.01
print('Average of {:.4g}pi rad and {:.4g}pi rad = {:.4g}pi rad'.format(theta1, theta2, interp_angle(theta1*np.pi, theta2*np.pi, 0.5)/np.pi))
theta1, theta2 = 0.1, -0.1
print('Average of {:.4g}pi rad and {:.4g}pi rad = {:.4g}pi rad'.format(theta1, theta2, interp_angle(theta1*np.pi, theta2*np.pi, 0.5)/np.pi))
theta1, theta2 = 0.1, 2-0.1
print('Average of {:.4g}pi rad and {:.4g}pi rad = {:.4g}pi rad'.format(theta1, theta2, interp_angle(theta1*np.pi, theta2*np.pi, 0.5)/np.pi))
Дает мне:
Average of 0pi rad and 0.5pi rad = 0.25pi rad
Average of 0pi rad and 0.99pi rad = 0.495pi rad
Average of 0pi rad and 1.01pi rad = 1.505pi rad
Average of 0.1pi rad and -0.1pi rad = 0pi rad
Average of 0.1pi rad and 1.9pi rad = 0pi rad
Моя личная рекомендация ?: Не надо! Подобно трехмерному вращению с углами Эйлера, я считаю, что использование абстракции более высокого измерения гораздо менее подвержено ошибкам и намного проще в реализации. В этом случае вместо кватернионов просто используйте простой двумерный вектор, выполните линейную интерполяцию вектора (тривиальная и однозначная операция), а затем используйте atan2 для получения угла! Что-то вроде этого:
Vector2 interop=lerp(v1,v2);
float angle=atan2(interop.x,interop.y);
Где
v1, v2 два вектора, указывающие на разные точки на единичном круге, и
lerp()это просто ваша средняя функция линейной интерполяции. В зависимости от вашей среды у вас может быть или не быть доступа к векторным классам, но, если у вас есть хотя бы элементарный опыт в математике, основы очень тривиальны для реализации (и есть множество библиотек, если вас не беспокоят!). В качестве дополнительного бонуса вы можете легко изменить тип интерполяции, не вмешиваясь в какие-либо дополнительные условия и т. Д.
PS Я достаточно новичок в том, чтобы отвечать на вопросы по SO, поэтому я не уверен, приемлемо ли отвечать на вопрос, направляя кого-то к совершенно другому методу. Я видел, как это делается, но иногда это встречает сопротивление ...
Для этой проблемы, если у вас есть углы в диапазоне +-pi, используйте это:((end - start + pi)%tau + tau)%tau - pi
Мое решение пошло на градусы. В моем классе VarTracker
@classmethod
def shortest_angle(cls, start: float, end: float, amount: float):
""" Find shortest angle change around circle from start to end, the return
fractional part by amount.
VarTracker.shortest_angle(10, 30, 0.1) --> 2.0
VarTracker.shortest_angle(30, 10, 0.1) --> -2.0
VarTracker.shortest_angle(350, 30, 0.1) --> 4.0
VarTracker.shortest_angle(350, 30, 0.8) --> 32.0
VarTracker.shortest_angle(30, 350, 0.5) --> -20.0
VarTracker.shortest_angle(170, 190, 0.1) --> 2.0
VarTracker.shortest_angle(10, 310, 0.5) --> -30.0
"""
sa = ((((end - start) % 360) + 540) % 360) - 180;
return sa * amount;
@classmethod
def slerp(cls, current: float, target: float, amount: float):
""" Return the new value if spherical linear interpolation from current toward target, by amount, all in degrees.
This method uses abs(amount) so sign of amount is ignored.
current and target determine the direction of the lerp.
Wraps around 360 to 0 correctly.
Lerp from 10 degrees toward 30 degrees by 3 degrees
VarTracker.slerp(10, 30, 3.0) --> 13.0
Ignores sign of amount
VarTracker.slerp(10, 30, -3.0) --> 13.0
VarTracker.slerp(30, 10, 3.0) --> 27.0
Wraps around 360 correctly
VarTracker.slerp(350, 30, 6) --> 356.0
VarTracker.slerp(350, 30, 12) --> 2.0
VarTracker.slerp(30, 350, -35) --> 355.0
a = VarTracker.slerp(30, 3140, -35) --> 355.0
VarTracker.slerp(170, 190, 2) --> 172.0
VarTracker.slerp(10, 310, 12) --> 358.0
Wraps over 0 degrees correctly
VarTracker.slerp(-10, 10, 3) --> 353.0
VarTracker.slerp(10, -10, 12) --> 358
"""
a = VarTracker.shortest_angle(current, target, 1.0)
diff = target - current
if np.abs(amount) > np.abs(diff):
amount = diff
if a < 0:
amount = -np.abs(amount)
else:
amount = np.abs(amount)
ret = current + amount
while ret < 0:
ret = ret + 360
ret = ret % 360
return ret