Подберите самозапускающуюся модель NLS асимптотической регрессии в R
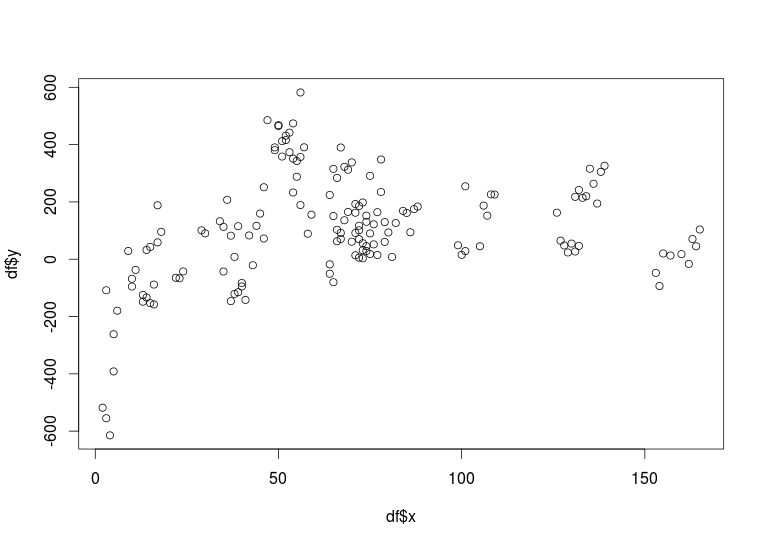
У меня есть датафрейм df
df<-structure(list(y = c(152.264522056852, 90.1433769206633, 14.9873599316925,
234.736409910023, 60.4167695627548, 380.654850683175, 467.840079978108,
358.497598990798, 431.528439198621, 442.010991849005, 351.189937948249,
343.098349086009, 357.122478995472, -518.123427070677, -554.919201846235,
-614.669225180172, -391.545088194311, -124.396037524566, 32.3765077856369,
43.199114789255, -88.3050879996736, 58.9395819107303, 162.441016515717,
116.965395963751, 13.0217520870501, 17.828320314642, -16.2957513090223,
70.6350404303521, 45.2225155929918, 103.825463471585, -47.560741043475,
-93.4213242912665, 20.1581508014351, 13.8083492300939, 5.60939206456533,
31.3564232334029, 28.6217511966825, -146.205068191513, -121.016505045118,
-115.100180697977, -82.8617020281963, -141.853484972846, -94.9308303585276,
-64.6400166181847, -66.4285516217351, -42.6337259062566, -148.123950563371,
-133.712445091456, -152.950761315413, -157.68036919646, -261.660716732062,
-179.565574658569, 130.724638285115, 291.076604684815, 121.960359405726,
164.323498383164, 348.140279591084, 129.706528767943, 93.6406692401506,
8.05810943059623, 126.535503963009, 162.629432365065, 64.9450473105535,
48.1501532075927, 23.6987462299876, 54.6846175976098, 26.9417262496427,
46.334381384775, 91.8543458277127, 70.0609471213538, 3.19760374492034,
45.6788141629659, 18.3098075923626, 51.8945797282504, 48.6587242824025,
15.2937245042995, 28.4606461951043, 28.9567997518461, -68.2299433113076,
-37.1677788909292, -108.258462657337, 100.907804159913, 90.3369144331664,
-50.4272195259109, 150.876719193533, 102.855497308774, 83.0877739411662,
-20.7788411897491, 116.68308432959, 159.48955539451, 72.2584278024733,
-17.8282854417339, -80.1063705889392, 62.7400574584608, 91.884871121496,
136.065904535353, 165.27273714263, 61.1652030013502, 192.680280862842,
101.131767969579, 55.857541423291, 233.031065647025, 287.956774678081,
189.082761215046, 390.740067397826, 89.1989531565923, 155.527563805692,
390.368216000032, 465.239609535784, 412.304880519398, 415.90913855657,
373.556777236925, 474.047956492752, 582.261698205024, 224.442115622107,
315.516411969438, 283.912847682368, 390.026366345584, 322.790248586796,
312.50101460889, 254.551377562806, 45.4501812993549, 187.152575587854,
152.183998291846, 226.360116416588, 225.67982583819, 132.601979068451,
-42.7843619789928, 82.2957233709167, 8.36848279205151, 115.376620422816,
-95.2025562002382, 217.845216980437, 241.779151081573, 214.481376983225,
219.953942558961, 315.959296110785, 263.547381375218, 194.449290025979,
305.158690313809, 326.318877183832, 251.31948431395, 485.374653904233,
188.342473105964, 95.6089326666552, 113.006237091264, 207.492174458399,
168.86071747914, 161.650970792165, 94.2879041660344, 174.897059062961,
183.964235268068, 70.9266221858561, 338.1149700284, 185.940875658067,
198.121665383659), x = c(74, 75, 77, 78, 79, 49, 50, 51, 52,
53, 54, 55, 56, 2, 3, 4, 5, 13, 14, 15, 16, 17, 71, 72, 157,
160, 162, 163, 164, 165, 153, 154, 155, 71, 72, 73, 74, 37, 38,
39, 40, 41, 40, 22, 23, 24, 13, 14, 15, 16, 5, 6, 74, 75, 76,
77, 78, 79, 80, 81, 82, 126, 127, 128, 129, 130, 131, 132, 71,
72, 73, 74, 75, 76, 99, 100, 101, 9, 10, 11, 3, 29, 30, 64, 65,
66, 42, 43, 44, 45, 46, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73,
54, 55, 56, 57, 58, 59, 49, 50, 51, 52, 53, 54, 56, 64, 65, 66,
67, 68, 69, 101, 105, 106, 107, 108, 109, 34, 35, 37, 38, 39,
10, 131, 132, 133, 134, 135, 136, 137, 138, 139, 46, 47, 17,
18, 35, 36, 84, 85, 86, 87, 88, 67, 70, 72, 73)), .Names = c("y",
"x"), row.names = c(719L, 720L, 721L, 722L, 723L, 724L, 725L,
726L, 727L, 728L, 729L, 730L, 731L, 732L, 733L, 734L, 735L, 736L,
737L, 738L, 739L, 740L, 741L, 742L, 743L, 744L, 745L, 746L, 747L,
748L, 749L, 750L, 751L, 752L, 753L, 754L, 755L, 756L, 757L, 758L,
759L, 760L, 761L, 762L, 763L, 764L, 765L, 766L, 767L, 768L, 769L,
770L, 771L, 772L, 773L, 774L, 775L, 776L, 777L, 778L, 779L, 780L,
781L, 782L, 783L, 784L, 785L, 786L, 787L, 788L, 789L, 790L, 791L,
792L, 799L, 800L, 801L, 802L, 803L, 804L, 805L, 806L, 807L, 808L,
809L, 810L, 814L, 815L, 816L, 817L, 818L, 819L, 820L, 821L, 822L,
823L, 824L, 825L, 826L, 827L, 828L, 849L, 850L, 851L, 852L, 853L,
854L, 867L, 868L, 869L, 870L, 871L, 872L, 873L, 874L, 875L, 876L,
877L, 878L, 879L, 881L, 882L, 883L, 884L, 885L, 886L, 887L, 888L,
889L, 890L, 891L, 914L, 924L, 925L, 926L, 927L, 928L, 929L, 930L,
931L, 932L, 933L, 934L, 936L, 937L, 938L, 939L, 944L, 945L, 946L,
947L, 948L, 949L, 950L, 951L, 952L), class = "data.frame")
Сейчас я пытаюсь приспособить модель асимптотической регрессии к моим данным, используя SSasympOff функция в R
fit<-nls(y ~ SSasympOff(x, A, lrc, c0), data = df)
Тем не менее, подгонка как-то не удалась, хотя я думал, что модель асимптотической регрессии может действительно соответствовать моим данным. Есть идеи, что не так?
1 ответ
Решение
Решение довольно простое. Мои данные должны соответствовать модели Вейбулла.
Вот ответ:
fit<-nls(y ~ SSweibull(x, A, lrc, c0), data = df