imresize - пытается понять бикубическую интерполяцию

Question

Я пытаюсь понять функцию:

function [weights, indices] = contributions(in_length, out_length, ...
                                            scale, kernel, ...
                                            kernel_width, antialiasing)


if (scale < 1) && (antialiasing)
    % Use a modified kernel to simultaneously interpolate and
    % antialias.
    h = @(x) scale * kernel(scale * x);
    kernel_width = kernel_width / scale;
else
    % No antialiasing; use unmodified kernel.
    h = kernel;
end

Я не очень понимаю, что означает эта строка

 h = @(x) scale * kernel(scale * x);

моя шкала 0,5
ядро кубическое.

Но кроме того, что это значит? Я думаю, что это похоже на создание функции, которая будет вызываться позже?

Answer 1

imresize выполняет сглаживание при уменьшении размера изображения, просто расширяя кубическое ядро, а не дискретный этап предварительной обработки.

Для kernel_width 4 пикселя (8 после перемасштабирования), где contributions функция использует 10 соседей для каждого пикселя, kernel против h (масштабированное ядро) выглядит как (ненормализовано, игнорировать ось X):

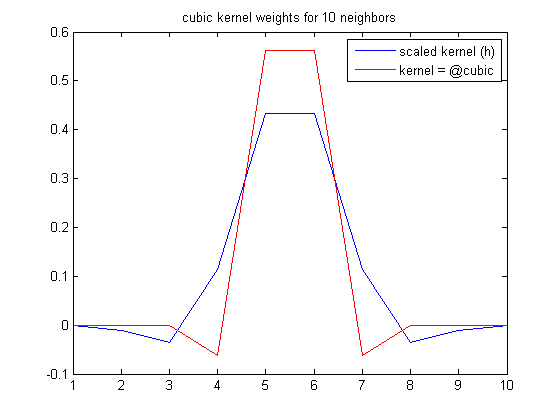
Это проще, чем первое выполнение фильтра нижних частот или гауссовой свертки на отдельном этапе предварительной обработки.

Кубическое ядро ​​определяется в нижней части imresize.m как:

function f = cubic(x)
% See Keys, "Cubic Convolution Interpolation for Digital Image
% Processing," IEEE Transactions on Acoustics, Speech, and Signal
% Processing, Vol. ASSP-29, No. 6, December 1981, p. 1155.

absx = abs(x);
absx2 = absx.^2;
absx3 = absx.^3;

f = (1.5*absx3 - 2.5*absx2 + 1) .* (absx <= 1) + ...
                (-0.5*absx3 + 2.5*absx2 - 4*absx + 2) .* ...
                ((1 < absx) & (absx <= 2));

PDF ссылочной статьи.

Соответствующей частью является уравнение (15):

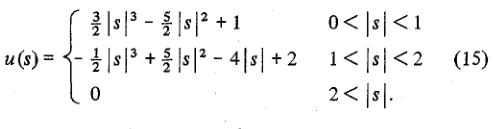
Это конкретная версия общих интерполяционных уравнений для a = -0.5 в следующих уравнениях:

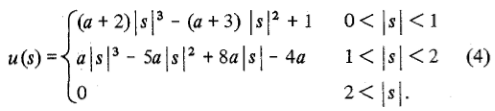
a обычно устанавливается на -0,5 или -0,75. Обратите внимание, что a = -0.5 соответствует кубическому сплайну Эрмита, который будет непрерывным и будет иметь непрерывный первый производный. OpenCV, похоже, использует -0,75.

Однако если вы отредактируете [OPENCV_SRC]\modules\imgproc\src\imgwarp.cpp и измените код:

static inline void interpolateCubic( float x, float* coeffs )
{
    const float A = -0.75f;
    ...

чтобы:

static inline void interpolateCubic( float x, float* coeffs )
{
    const float A = -0.50f;
    ...

и пересоберите OpenCV (совет: отключите CUDA и модуль gpu на короткое время компиляции), после чего вы получите те же результаты. Смотрите соответствующий результат в моем другом ответе на связанный вопрос от ОП.

Answer 2

Это своего рода продолжение ваших предыдущих вопросов о разнице между imresize в MATLAB и cv::resize в OpenCV дана бикубическая интерполяция.

Я был заинтересован в выяснении, почему есть разница. Это мои выводы (как я понял алгоритмы, пожалуйста, исправьте меня, если я сделаю какие-либо ошибки).

---

Думайте об изменении размера изображения как о плоском преобразовании от входного изображения размера M-by-N на выходное изображение размером scaledM-by-scaledN,

Проблема в том, что точки не обязательно помещаются на дискретной сетке, поэтому для получения интенсивностей пикселей в выходном изображении нам необходимо интерполировать значения некоторых соседних выборок (обычно выполняемых в обратном порядке, то есть для каждой В выходном пикселе мы находим соответствующую нецелую точку во входном пространстве и интерполируем ее).

Это где алгоритмы интерполяции различаются, выбирая размер окрестности и весовые коэффициенты, дающие каждой точке в этой окрестности. Отношение может быть первого или более высокого порядка (где задействованная переменная - это расстояние от нецелочисленной выборки с обратным отображением до дискретных точек на исходной сетке изображения). Обычно вы назначаете более высокие веса более близким точкам.

Смотря на imresize в MATLAB вот весовые функции для линейного и кубического ядер:

function f = triangle(x)
    % or simply: 1-abs(x) for x in [-1,1]
    f = (1+x) .* ((-1 <= x) & (x < 0)) + ...
        (1-x) .* ((0 <= x) & (x <= 1));
end

function f = cubic(x)
    absx = abs(x);
    absx2 = absx.^2;
    absx3 = absx.^3;
    f = (1.5*absx3 - 2.5*absx2 + 1) .* (absx <= 1) + ...
        (-0.5*absx3 + 2.5*absx2 - 4*absx + 2) .* ((1 < absx) & (absx <= 2));
end

(Они в основном возвращают вес интерполяции выборки в зависимости от того, как далеко она находится от интерполированной точки.)

Вот как выглядят эти функции:

>> subplot(121), ezplot(@triangle,[-2 2])  % triangle
>> subplot(122), ezplot(@cubic,[-3 3])     % Mexican hat

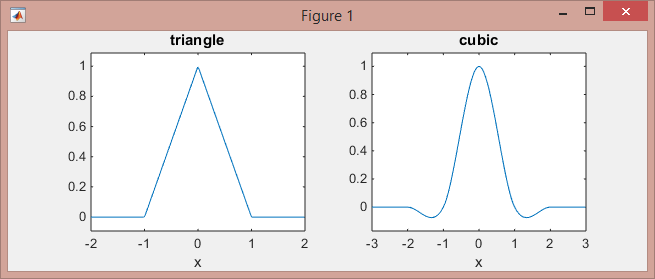
Обратите внимание, что линейное ядро ​​(кусочно-линейные функции на интервалах [-1,0] и [0,1] и нули в других местах) работает в 2-соседних точках, тогда как кубическое ядро ​​(кусочно-кубические функции на интервалы [-2,-1], [-1,1], [1,2] и нули в других местах) работают в 4 соседних точках.

Вот иллюстрация для одномерного случая, показывающая, как интерполировать значение x из дискретных точек f(x_k) используя кубическое ядро:

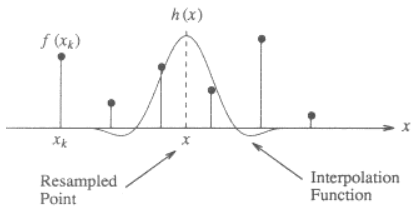
Функция ядра h(x) сосредоточено в x, местоположение точки, которая должна быть интерполирована. Интерполированное значение f(x) взвешенная сумма дискретных соседних точек (2 слева и 2 справа), масштабированная по значению интерполяционной функции в этих дискретных точках.

Скажи, если расстояние между x и ближайшая точка d (0 <= d < 1), интерполированное значение в местоположении x будет:

f(x) = f(x1)*h(-d-1) + f(x2)*h(-d) + f(x3)*h(-d+1) + f(x4)*h(-d+2)

где порядок точек изображен ниже (обратите внимание, что x(k+1)-x(k) = 1):

x1      x2   x    x3       x4
o--------o---+----o--------o
         \___/
       distance d

Теперь, поскольку точки дискретны и дискретизируются с одинаковыми интервалами, а ширина ядра обычно мала, интерполяция может быть сформулирована кратко как операция свертки:

Концепция распространяется на 2 измерения просто путем интерполяции сначала по одному измерению, а затем интерполяции по другому измерению с использованием результатов предыдущего шага.

Вот пример билинейной интерполяции, которая в 2D рассматривает 4 соседние точки:

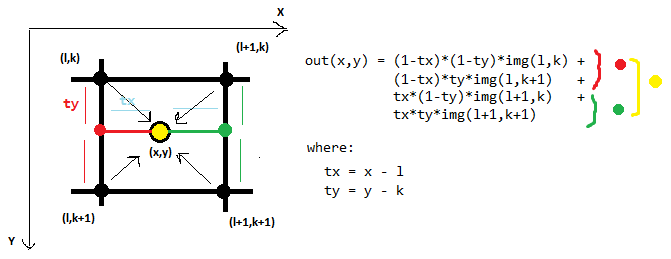
Бикубическая интерполяция в 2D использует 16 соседних точек:

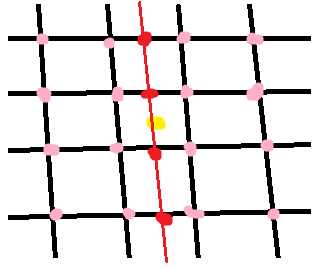
Сначала мы интерполируем вдоль строк (красные точки), используя 16 образцов сетки (розовый). Затем мы интерполируем по другому измерению (красная линия), используя интерполированные точки из предыдущего шага. На каждом этапе выполняется регулярная 1D-интерполяция. В этом уравнение слишком длинное и сложное, чтобы я мог разобрать его вручную!

---

Теперь, если мы вернемся к cubic Функция в MATLAB фактически соответствует определению ядра свертки, приведенному в справочном документе как уравнение (4). Вот то же самое, взятое из Википедии:

Вы можете видеть, что в приведенном выше определении MATLAB выбрал значение a=-0.5,

Теперь разница между реализацией в MATLAB и OpenCV заключается в том, что OpenCV выбрал значение a=-0.75,

static inline void interpolateCubic( float x, float* coeffs )
{
    const float A = -0.75f;

    coeffs[0] = ((A*(x + 1) - 5*A)*(x + 1) + 8*A)*(x + 1) - 4*A;
    coeffs[1] = ((A + 2)*x - (A + 3))*x*x + 1;
    coeffs[2] = ((A + 2)*(1 - x) - (A + 3))*(1 - x)*(1 - x) + 1;
    coeffs[3] = 1.f - coeffs[0] - coeffs[1] - coeffs[2];
}

Это может быть неочевидно сразу, но код вычисляет члены кубической функции свертки (перечислены сразу после уравнения (25) в статье):

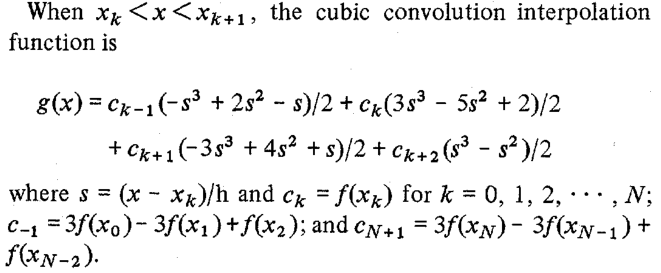
Мы можем проверить это с помощью Symbolic Math Toolbox:

A = -0.5;
syms x
c0 = ((A*(x + 1) - 5*A)*(x + 1) + 8*A)*(x + 1) - 4*A;
c1 = ((A + 2)*x - (A + 3))*x*x + 1;
c2 = ((A + 2)*(1 - x) - (A + 3))*(1 - x)*(1 - x) + 1;
c3 = 1 - c0 - c1 - c2;

Эти выражения могут быть переписаны как:

>> expand([c0;c1;c2;c3])
ans =
       - x^3/2 + x^2 - x/2
 (3*x^3)/2 - (5*x^2)/2 + 1
 - (3*x^3)/2 + 2*x^2 + x/2
             x^3/2 - x^2/2

которые соответствуют условиям из уравнения выше.

Очевидно, что разница между MATLAB и OpenCV сводится к использованию другого значения для свободного термина a, По мнению авторов статьи, значение 0.5 является предпочтительным выбором, потому что он подразумевает лучшие свойства для ошибки аппроксимации, чем любой другой выбор для a,