Есть ли встроенный Matlab, который вычисляет квадратичную форму (x'*A*x)?
Довольно простой вопрос: учитывая N x N симметричную матрицу A и N-вектор x, есть ли встроенная функция Matlab для вычисления x'*A*x? т.е. вместо y = x'*A*xесть ли функция quadraticform улица y = quadraticform(A, x)?
Очевидно, я могу просто сделать y = x'*A*x, но мне нужна производительность, и, похоже, должен быть способ воспользоваться
Aсимметричный- Левый и правый множители - это один и тот же вектор
Если нет ни одной встроенной функции, есть ли метод, который быстрее, чем x'*A*x? ИЛИ, достаточно ли умен синтаксический анализатор Matlab для оптимизации x'*A*x? Если да, можете ли вы указать мне место в документации, которая подтверждает этот факт?
3 ответа
Я не мог найти такую встроенную функцию, и у меня есть идея, почему.
y=x'*A*x можно записать в виде суммы n^2 термины A(i,j)*x(i)*x(j), где i а также j бежит из 1 в n (где A является nxn матрица). A симметрично: A(i,j) = A(j,i) для всех i а также j, Из-за симметрии каждый член появляется в сумме дважды, за исключением тех, где i равняется j, Итак, мы имеем n*(n+1)/2 разные условия. У каждого есть два умножения с плавающей точкой, поэтому наивный метод должен n*(n+1) умножения в общей сложности. Легко видеть, что наивный расчет x'*A*xто есть расчет z=A*x а потом y=x'*zТакже необходимо n*(n+1) умножения. Тем не менее, есть более быстрый способ суммировать наши n*(n+1)/2 разные термины: для каждого iмы можем вынести x(i), что означает, что только n*(n-1)/2+3*n умножения достаточно. Но это не очень помогает: время выполнения расчета y=x'*A*x все еще O(n^2),
Итак, я думаю, что вычисление квадратичных форм не может быть сделано быстрее, чем O(n^2)и так как это также может быть достигнуто по формуле y=x'*A*x, не было бы реального преимущества специальной функции "квадратичной формы".
=== ОБНОВЛЕНИЕ ===
Я написал функцию "quadraticform" в C, как расширение Matlab:
// y = quadraticform(A, x)
#include "mex.h"
/* Input Arguments */
#define A_in prhs[0]
#define x_in prhs[1]
/* Output Arguments */
#define y_out plhs[0]
void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[])
{
mwSize mA, nA, n, mx, nx;
double *A, *x;
double z, y;
int i, j, k;
if (nrhs != 2) {
mexErrMsgTxt("Two input arguments required.");
} else if (nlhs > 1) {
mexErrMsgTxt("Too many output arguments.");
}
mA = mxGetM(A_in);
nA = mxGetN(A_in);
if (mA != nA)
mexErrMsgTxt("The first input argument must be a quadratic matrix.");
n = mA;
mx = mxGetM(x_in);
nx = mxGetN(x_in);
if (mx != n || nx != 1)
mexErrMsgTxt("The second input argument must be a column vector of proper size.");
A = mxGetPr(A_in);
x = mxGetPr(x_in);
y = 0.0;
k = 0;
for (i = 0; i < n; ++i)
{
z = 0.0;
for (j = 0; j < i; ++j)
z += A[k + j] * x[j];
z *= x[i];
y += A[k + i] * x[i] * x[i] + z + z;
k += n;
}
y_out = mxCreateDoubleScalar(y);
}
Я сохранил этот код как "quadraticform.c" и скомпилировал его с помощью Matlab:
mex -O quadraticform.c
Я написал простой тест производительности, чтобы сравнить эту функцию с x 'A x:
clear all; close all; clc;
sizes = int32(logspace(2, 3, 25));
nsizes = length(sizes);
etimes = zeros(nsizes, 2); % Matlab vs. C
nrepeats = 100;
h = waitbar(0, 'Please wait...');
for i = 1 : nrepeats
for j = 1 : nsizes
n = sizes(j);
A = randn(n);
A = (A + A') / 2;
x = randn(n, 1);
if randn > 0
start = tic;
y1 = x' * A * x;
etimes(j, 1) = etimes(j, 1) + toc(start);
start = tic;
y2 = quadraticform(A, x);
etimes(j, 2) = etimes(j, 2) + toc(start);
else
start = tic;
y2 = quadraticform(A, x);
etimes(j, 2) = etimes(j, 2) + toc(start);
start = tic;
y1 = x' * A * x;
etimes(j, 1) = etimes(j, 1) + toc(start);
end;
if abs((y1 - y2) / y2) > 1e-10
error('"x'' * A * x" is not equal to "quadraticform(A, x)"');
end;
waitbar(((i - 1) * nsizes + j) / (nrepeats * nsizes), h);
end;
end;
close(h);
clear A x y;
etimes = etimes / nrepeats;
n = double(sizes);
n2 = n .^ 2.0;
i = nsizes - 2 : nsizes;
n2_1 = mean(etimes(i, 1)) * n2 / mean(n2(i));
n2_2 = mean(etimes(i, 2)) * n2 / mean(n2(i));
figure;
loglog(n, etimes(:, 1), 'r.-', 'LineSmoothing', 'on');
hold on;
loglog(n, etimes(:, 2), 'g.-', 'LineSmoothing', 'on');
loglog(n, n2_1, 'k-', 'LineSmoothing', 'on');
loglog(n, n2_2, 'k-', 'LineSmoothing', 'on');
axis([n(1) n(end) 1e-4 1e-2]);
xlabel('Matrix size, n');
ylabel('Running time (a.u.)');
legend('x'' * A * x', 'quadraticform(A, x)', 'O(n^2)', 'Location', 'NorthWest');
W = 16 / 2.54; H = 12 / 2.54; dpi = 100;
set(gcf, 'PaperPosition', [0, 0, W, H]);
set(gcf, 'PaperSize', [W, H]);
print(gcf, sprintf('-r%d',dpi), '-dpng', 'quadraticformtest.png');
Результат очень интересный. Время работы обоих x'*A*x а также quadraticform(A,x) сходится к O(n^2), но у первого есть меньший фактор:
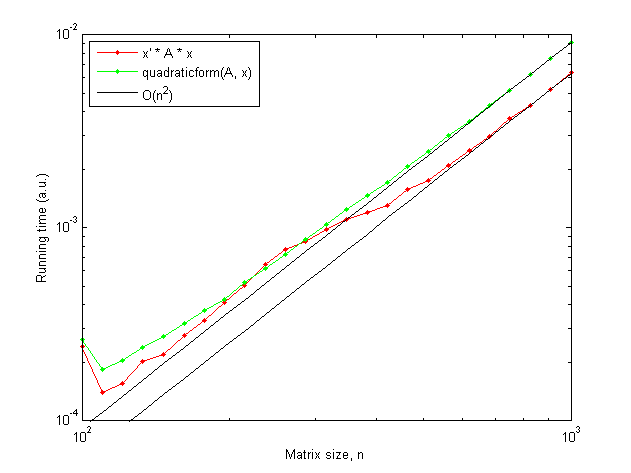
MATLAB достаточно умен, чтобы распознавать и оптимизировать некоторые виды выражений составных матриц, и я полагаю (хотя я не могу определенно подтвердить), что квадратичная форма является одной из оптимизаций, которые она делает.
Тем не менее, MathWorks не склонна документировать это, потому что: а) он, как правило, оптимизируется только внутри функций, а не в скриптах, в командной строке или при отладке; б) он может работать только при некоторых обстоятельствах, например, для реального A) это может меняться от выпуска к выпуску, поэтому они не хотят, чтобы вы полагались на него; г) это одна из фирменных вещей, которые делают MATLAB таким хорошим.
Чтобы подтвердить, вы можете попробовать сравнить время y=x'*A*x против B=A*x; y=x'*B, Вы также можете попробовать feature('accel','off'), который отключит большинство подобных оптимизаций.
Наконец, если вы обратитесь в службу поддержки MathWorks, вы можете попросить одного из разработчиков подтвердить, проводится ли оптимизация.
Я не уверен, сработает ли это в вашем случае, но я столкнулся с похожей ситуацией, когда я хотел вычислить много сумм квадратов. После работы с алгеброй я понял, что подхожу к этому как математик, а не как компьютерный инженер:
Если строки X ваши точки данных, то i- й ряд Q ниже будет i- я сумма:
Q = sum(X.^2 * A)
Надеюсь, это поможет!