Определите, лежит ли угол между двумя другими углами
Я пытаюсь выяснить, лежит ли угол между двумя другими углами. Я пытался создать простую функцию для выполнения этого, но ни один из моих методов не будет работать для всех возможных значений углов.
Можете ли вы помочь мне отредактировать мою функцию, чтобы правильно определить, лежит ли угол между двумя другими углами?
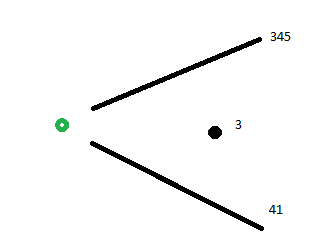
На изображении выше; Я использую зеленую точку в качестве центральной, затем определяю угол каждой линии к зеленой точке. Затем я вычисляю угол черной точки к зеленой точке. Я пытаюсь проверить, равен ли угол черной точки между двумя линиями.
ПРИМЕЧАНИЕ: в моем случае;говорят, что угол (targetAngle) лежит между двумя другими углами, ЕСЛИ разница между двумя углами составляет < 180 градусов, а targetAngle находится в полости, образованной этими двумя углами.
Следующий код должен работать, но он терпит неудачу для них (которые лежат между углом):
- is_angle_between (150, 190, 110)
- is_angle_between (3, 41, 345)
bool is_angle_between(int target, int angle1, int angle2)
{
int rAngle1 = ((iTarget - iAngle1) % 360 + 360) % 360;
int rAngle2 = ((iAngle2 - iAngle1) % 360 + 360) % 360;
return (0 <= rAngle1 && rAngle1 <= rAngle2);
}
// Example usage
is_angle_between(3, 41, 345);
Я попробовал еще одну технику, которая тоже не работает:
int is_angle_between(int target, int angle1, int angle2)
{
int dif1 = angle1-angle2;
int dif2 = angle2-angle1;
int uDif1 = convert_to_positive_angle( dif1 ); // for eg; convert -15 to 345
int uDif2 = convert_to_positive_angle( dif2 );
if (uDif1 <= uDif2) {
if (dif1 < 0) {
return (target <= angle1 && target >= angle2);
}
else return (in_between_numbers(iTarget, iAngle1, iAngle2));
}
else {
if (dif2 < 0) {
return (target <= angle1 && target >= angle2);
}
else return (in_between_numbers(iTarget, iAngle1, iAngle2));
}
return -1;
}
12 ответов
bool is_angle_between(int target, int angle1, int angle2)
{
// make the angle from angle1 to angle2 to be <= 180 degrees
int rAngle = ((angle2 - angle1) % 360 + 360) % 360;
if (rAngle >= 180)
std::swap(angle1, angle2);
// check if it passes through zero
if (angle1 <= angle2)
return target >= angle1 && target <= angle2;
else
return target >= angle1 || target <= angle2;
}
Вдохновленный пост об Интервалы в модульной арифметике:
static bool is_angle_between(int x, int a, int b) {
b = modN(b - a);
x = modN(x - a);
if (b < 180) {
return x < b;
} else {
return b < x;
}
}
где (в случае проверки углов) modN() будет реализован как
// modN(x) is assumed to calculate Euclidean (=non-negative) x % N.
static int modN(int x) {
const int N = 360;
int m = x % N;
if (m < 0) {
m += N;
}
return m;
}
void normalize( float& angle )
{
while ( angle < -180 ) angle += 360;
while ( angle > 180 ) angle -= 360;
}
bool isWithinRange( float testAngle, float a, float b )
{
a -= testAngle;
b -= testAngle;
normalize( a );
normalize( b );
if ( a * b >= 0 )
return false;
return fabs( a - b ) < 180;
}
Если бы angle2 всегда был 0, а angle1 всегда был между 0 и 180, это было бы легко:
return angle1 < 180 && 0 < target && target < angle1;
если я правильно читаю требования.
Но добраться не так сложно.
int reduced1 = (angle1 - angle2 + 360) % 360; // and imagine reduced2 = 0
if (180 < reduced1) { angle2 = angle1; reduced1 = 360 - reduced1; } // swap if backwards
int reducedTarget = (target - angle2 + 360) % 360;
return reduced1 < 180 && 0 < reducedTarget && reducedTarget < reduced1;
Все топовые ответы здесь неверны. Поэтому я чувствую, что мне необходимо опубликовать ответ.
Я просто публикую часть ответа, который я разместил здесь: /questions/38312451/yavlyaetsya-li-ugol-mezhdu-dvumya-uglami/38312454#38312454 Этот ответ также относится к случаю, когда вы уже знаете, какой угол находится слева и справа от рефлексивный угол. Но вам также необходимо определить, какая сторона угла является какой.
1-й, чтобы найти крайний левый угол, если любое из этих утверждений верно angle1 Ваш самый левый угол:
angle1 <= angle2 && angle2 - angle1 <= PIangle1 > angle2 && angle1 - angle2 >= PI
Для простоты предположим, что ваш самый левый угол равен l, а самый правый угол - r, и вы пытаетесь определить, находится ли g между ними.
Проблема здесь, кажется. По сути, мы ищем 3 положительных случая:
- l ≤ g ≤ r
- l ≤ g ∧ r
- g ≤ r ∧ r
Поскольку вы вычисляете левую и правую части угла, вы заметите, что здесь есть возможность оптимизации при одновременном выполнении обоих процессов. Ваша функция будет выглядеть так:
if(angle1 <= angle2) {
if(angle2 - angle1 <= PI) {
return angle1 <= target && target <= angle2;
} else {
return angle2 <= target || target <= angle1;
}
} else {
if(angle1 - angle2 <= PI) {
return angle2 <= target && target <= angle1;
} else {
return angle1 <= target || target <= angle2;
}
}
Или, если вам это нужно, вы можете перейти в это кошмарное состояние:
angle1 <= angle2 ?
(angle2 - angle1 <= PI && angle1 <= target && target <= angle2) || (angle2 - angle1 > PI && (angle2 <= target || target <= angle1)) :
(angle1 - angle2 <= PI && angle2 <= target && target <= angle1) || (angle1 - angle2 > PI && (angle1 <= target || target <= angle2))
Обратите внимание, что вся эта математика предполагает, что ваш ввод в радианах и в диапазоне [0: 2π].
Я делал это раньше, сравнивая углы.
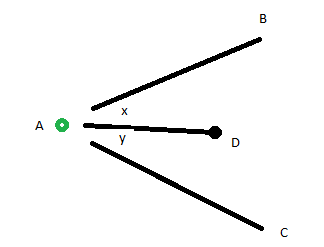
На рисунке выше вектор AD будет между AB и AC, если и только если
angle BAD + angle CAD == angle BAC
Из-за неточностей с плавающей запятой я сравнил значения после округления их сначала, чтобы сказать 5 десятичных знаков.
Таким образом, сводится к наличию алгоритма угла между двумя векторами p а также q который просто выражается как:
double a = p.DotProduct(q);
double b = p.Length() * q.Length();
return acos(a / b); // radians
Я оставлю вычисления векторов DotProduct и Length в качестве упражнения по поиску в Google. И вы получаете векторы, просто вычитая координаты одного терминала из другого.
Конечно, вы должны сначала проверить, параллельны ли AB и AC или нет.
Если угол T между углами A и B, всегда есть два ответа: истина и ложь.
Нам нужно указать, что мы имеем в виду, и в этом случае мы ищем нормализованные малые углы развертки и находится ли наш угол между этими значениями. Учитывая любые два угла, между ними существует угол отражения, находится ли нормализованное значение T в пределах этого угла отражения?
Если мы повернем A и B и T так, что T = 0, и нормализуем A и B с точностью до +-полудня (180° или 2PI). Тогда наш ответ таков: имеют ли А и В разные знаки и находятся ли они в полукруглой окружности друг от друга.
Если мы вычтем угол из теста, то добавим 180° (так, что A относительно T+180). Затем мы модифицируем на 360, давая нам диапазон между [-360°,360°], добавляем 360 ° и снова мод (обратите внимание, вы также можете просто проверить, является ли он отрицательным, и добавить 360, если он есть), давая нам значение, которое наверняка будет [0°,360°]. Мы вычитаем 180 °, давая нам значение между [-180°,180°] относительно T+180°-180° aka, т.е. Т. Теперь угол равен нулю, и все углы попадают в нормализованный диапазон. Теперь мы проверяем, чтобы углы изменили знак, и чтобы они были не более чем на 180 ° друг от друга, у нас есть наш ответ.
Потому что вопрос задается в C++:
bool isAngleBetweenNormalizedSmallSweepRange(int test, int a, int b) {
int a_adjust = ((((a - test + 180)) % 360) + 360) % 360 - 180;
int b_adjust = ((((b - test + 180)) % 360) + 360) % 360 - 180;
return ((a_adjust ^ b_adjust) < 0) && ((a_adjust - b_adjust) < 180) && ((a_adjust - b_adjust) > -180);
}
Мы также можем сделать несколько трюков, чтобы упростить код и избежать ненужных операций по модулю (см. Комментарии ниже). Нормализация переместит угол a в диапазон [-180°,180°] относительно угла t.
int normalized(int a, int test) {
int n = a - test + 180;
if ((n > 360) || (n < -360)) n %= 360;
return (n > 0)? n - 180: n + 180;
}
bool isAngleBetweenNormalizedSmallSweepRange(int test, int a, int b) {
int a_adjust = normalized(a,test);
int b_adjust = normalized(b,test);
return ((a_adjust ^ b_adjust) < 0) &&
((a_adjust > b_adjust)? a_adjust-b_adjust: b_adjust-a_adjust) < 180;
}
Также, если мы можем быть уверены, что диапазон равен [0,360], мы можем обойтись более простым оператором if
bool isAngleBetweenNormalizedSmallSweepRange(int test, int a, int b) {
int dA = a - test + 180;
if (dA > 360) {
dA -= 360;
}
int a_adjust = (dA > 0) ? dA - 180 : dA + 180;
int dB = b - test + 180;
if (dB > 360) {
dB -= 360;
}
int b_adjust = (dB > 0) ? dB - 180 : dB + 180;
return ((a_adjust ^ b_adjust) < 0)
&& ((a_adjust > b_adjust) ? a_adjust - b_adjust : b_adjust - a_adjust) < 180;
}
Я знаю, что этот пост старый, но, кажется, нет принятого ответа, и я нашел следующий подход достаточно надежным. Хотя это может быть больше, чем вам нужно. Он поддерживает диапазоны углов больше 180 градусов (а также больше 360 градусов и отрицательных углов). Он также поддерживает десятичную точность.
Метод использует это normalize() вспомогательная функция для преобразования углов в правильное пространство:
float normalize( float degrees )
{
//-- Converts the specified angle to an angle between 0 and 360 degrees
float circleCount = (degrees / 360.0f);
degrees -= (int)circleCount * 360;
if( 0.0f > degrees )
{
degrees += 360.0f;
}
return degrees;
}
Вот решение:
bool isWithinRange( float start, float end, float angle )
{
if( fabsf( end - start ) >= 360.0f )
{
//-- Ranges greater or equal to 360 degrees cover everything
return true;
}
//-- Put our angle between 0 and 360 degrees
float degrees = normalize( angle );
//-- Resolve degree value for the start angle; make sure it's
// smaller than our angle.
float startDegrees = normalize( start );
if( startDegrees > degrees )
{
startDegrees -= 360.0f;
}
//-- Resolve degree value for the end angle to be within the
// same 360 degree range as the start angle and make sure it
// comes after the start angle.
float endDegrees = normalize( end );
if( endDegrees < startDegrees )
{
endDegrees += 360.0f;
}
else if( (endDegrees - startDegrees) >= 360.0f )
{
endDegrees -= 360.0f;
}
//-- All that remains is to validate that our angle is between
// the start and the end.
if( (degrees < startDegrees) || (degrees > endDegrees) )
{
return false;
}
return true;
}
Надеюсь, это кому-нибудь поможет.
Используя тот же стиль функций, что и в вашем вопросе, мне повезло со следующими методами:
public static bool IsInsideRange(double testAngle, double startAngle, double endAngle)
{
var a1 = System.Math.Abs(AngleBetween(startAngle, testAngle));
var a2 = System.Math.Abs(AngleBetween(testAngle, endAngle));
var a3 = System.Math.Abs(AngleBetween(startAngle, endAngle));
return a1 + a2 == a3;
}
public static double AngleBetween(double start, double end)
{
return (end - start) % 360;
}
Я нашел эту цитату из этой темы:
если точка P находится внутри треугольника ABC, то
Зона PAB+ Зона PBC + Зона PAC= Зона ABC
обратите внимание, что если P находится на краю AB, BC или CA, то вышеупомянутое удержание. Но фактически одна из областей PAB, PBC, PAC равна 0 (поэтому просто убедитесь, что вы проверили это).
если P снаружи, указанное выше равенство НЕ выполняется...
Как определить площадь? у вас есть два варианта: 1) теорема Херона, включает в себя sqrt, медленнее 2) более предпочтительный путь - это перекрестные произведения (или, фактически, половина абсолютного значения (сумма отрицательных произведений минус сумма восходящих произведений))
например, если A=(x1,y1) B=(x2,y2), C=(x3,y3) Area= abs(x1*y2+x2*y3+x3*y1-x1*y3-x3*y2- х2 * у1)/2
также вы можете быть осторожны с ошибками с плавающей запятой... вместо проверки на строгое неравенство, проверьте на абс (ba)
Надеюсь, это поможет
Если у вас есть время, проверьте это:
bool AngleIsBetween(int firstAngle, int secondAngle, int targetAngle)
{
while (firstAngle >= 360)
firstAngle -= 360;
while (secondAngle >= 360)
secondAngle -= 360;
while (targetAngle >= 360)
targetAngle -=360;
while (firstAngle < 0)
firstAngle += 360;
while (secondAngle < 0)
secondAngle += 360;
while (targetAngle < 0)
targetAngle +=360;
int temp = secondAngle;
if (firstAngle > secondAngle)
{
secondAngle = firstAngle;
firstAngle = temp;
}
if ((secondAngle - firstAngle) > 180)
{
temp = secondAngle - 360;
secondAngle = firstAngle;
firstAngle = temp;
}
return ((targetAngle >= firstAngle) && (targetAngle <= secondAngle));
}
Измените параметры, чтобы плавать, если вам нужно.
У вас есть угол a а также cи не хочу видеть угол b находится между этими углами.
Вы можете рассчитать угол между a->b а также a->c, Если ∠a->c меньше чем ∠a->b, b должен быть между a а также c,
Расстояние между углами, a а также b
function distanceBetweenAngles(a, b) {
distance = b - a;
if (a > b) {
distance += 2*pi;
}
return distance;
}
Тогда вы можете сделать
// Checks if angle 'x' is between angle 'a' and 'b'
function isAngleBetween(x, a, b) {
return distanceBetweenAngles(a, b) >= distanceBetweenAngles(a, x);
}
Это предполагает, что вы используете радианы, а не градусы, как следует. Это удаляет много ненужного кода.