Вычисление суммы узлов в одной строке вертикали двоичного дерева
Для бинарного дерева я хочу получить сумму всех узлов, попадающих в одну строку вертикали. Я хочу, чтобы сумма узлов в каждом узле вертикали
A
/ \
B C
/ \ / \
D E F G
/ \
H I
Если вы смотрите на тройник выше
line 0 A E F so sum = A+E+F
line -1 B I so sum = B +I
line 1 C so sum = C
line 2 G so sum = G
Я реализовал следующий алгоритм
Map<Integer,Integere> mp = new HashMap<Integer,Integer>()
calculate(root,0);
void calculate(Node node, int pos){
if(node==null)
return ;
if(mp.containsKey(pos) ){
int val = mp.get(pos) + node.data;
mp.put(pos,val);
}
else{
mp.put(pos,node.data);
}
calculate(node.left,pos-1);
calculate(node.right,pos+1);
}
- Я думаю, что приведенный выше алгоритм в порядке. Может ли кто-нибудь подтвердить?
- Также, как я могу сделать это, не используя HashMap, arraylist или любой другой тип данных коллекции java. Один метод - два - два массива, один для хранения отрицательных индексов (сопоставленных с положительными) и один для положительных индексов (справа от корня). Но мы не знаю, какой будет размер массива.
- Один из подходов состоит в том, чтобы использовать двойной список ссылок и добавить узел при движении вправо / влево, если это необходимо. Не понимаю, как я могу реализовать этот подход? Любой другой простой / более эффективный по времени подход?
- Является ли сложность вышеприведенного кода, который я получил, O(n)? (не умею анализировать сложность времени, поэтому спрашиваю)
4 ответа
Код C++
int vertsum(Node* n, int cur_level, int target_level)
{
if (!n)
return 0;
int sum = 0;
if (cur_level == target_level)
sum = n->value;
return sum +
vertsum(n->left, cur_level-1, target_level) +
vertsum(n->right, cur_level+1, target_level);
}
пример вызова:
vertsum(root, 0, 1);
РЕДАКТИРОВАТЬ:
После уточнения требований, здесь предлагается код. Обратите внимание, что это C++, и он не совсем использует стандартный API Java или C++ для списков, но вы должны понять. Я предполагаю что addNodeBefore а также addNodeAfter инициализировать данные узла (т.е. ListNode::counter)
void vertsum(TreeNode* n, int level, ListNode& counter)
{
if (!n)
return;
counter.value += n->value;
counter.index = level;
if (! counter.prev)
addNodeBefore(counter);
vertsum(n->left, level-1, counter.prev);
if (! counter.next)
addNodeAfter(counter);
vertsum(n->right, level+1, counter.next);
return;
}
Вы можете посетить двоичное дерево в первом порядке глубины и использовать смещение, чтобы отслеживать, как далеко вы переместились влево / вправо относительно вашего начального узла. Каждый раз, когда вы двигаетесь влево, вы уменьшаете смещение, а каждый раз, когда вы двигаетесь вправо, вы увеличиваете смещение. Если ваша процедура посещения вызывается со смещением 0, тогда это означает, что посещаемый узел имеет то же смещение, что и начальный узел (т. е. он находится в том же столбце), и поэтому вы должны добавить его значение.
псевдокод:
procedure visit (node n, int offset) {
sumleft = 0
sumright = 0
if (n.left != null)
sumleft = visit(n.left, offset - 1)
if (n.right != null)
sumright = visit(n.right, offset + 1)
if (offset == 0)
return n.value + sumleft + sumright
else
return sumleft + sumright;
}
Например, если вы звоните
visit(A, 0)
Вы получите следующие звонки:
visit(A, 0) -> E.value + F.value + A.value
visit(B, -1) -> E.value
visit(D, -2) -> 0
visit(H, -3) -> 0
visit(I, +2) -> 0
visit(E, 0) -> E.value
visit(C, +1) -> F.value
visit(F, 0) -> F.value
visit(G, +1) -> 0
Другой пример, начиная с узла B:
visit(B, 0)
visit(D, -1)
visit(H, -2)
visit(I, 0) -> here we return I.value
visit(E, +1)
когда рекурсия возвращается к первоначальному вызову visit(B, 0) у нас есть sumleft = I.value а также sumright = 0итак мы возвращаем конечный результат B.value + I.value, как и ожидалось.
Сложность O(n), потому что вы посещаете один раз все узлы вашего дерева с корнем в начальном узле.
Подумав о вышеупомянутом алгоритме, я понимаю, что у него есть ограничение, которое становится очевидным, когда мы рассматриваем более сложное дерево, подобное следующему:
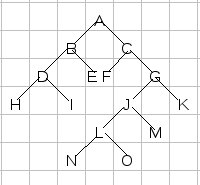
В этом случае visit(B, 0) все равно вернется B.value + I.value, но это не ожидаемый результат, потому что N также находится в том же столбце. Следующий алгоритм должен справиться с этой проблемой:
procedure visit(node n, int c, int t) {
sumleft = 0;
sumright = 0;
if (n.left != null)
sumleft = visit(n.left, c - 1, t)
if (n.right != null)
sumright = visit(n.right, c + 1, t)
if (c == t)
return n.value + sumleft + sumright;
else
return sumleft + sumright;
}
Идея по сути та же самая, но у нас теперь есть параметр c который дает текущий столбец и параметр t который является целевой колонкой. Если мы хотим, чтобы сумма элементов в B столбец, то мы можем позвонить visit(A, 0, -1)то есть мы всегда начинаем наш визит с узла A (дерево корня), которое находится в столбце 0, и наша цель - столбец -1. Мы получаем следующее:
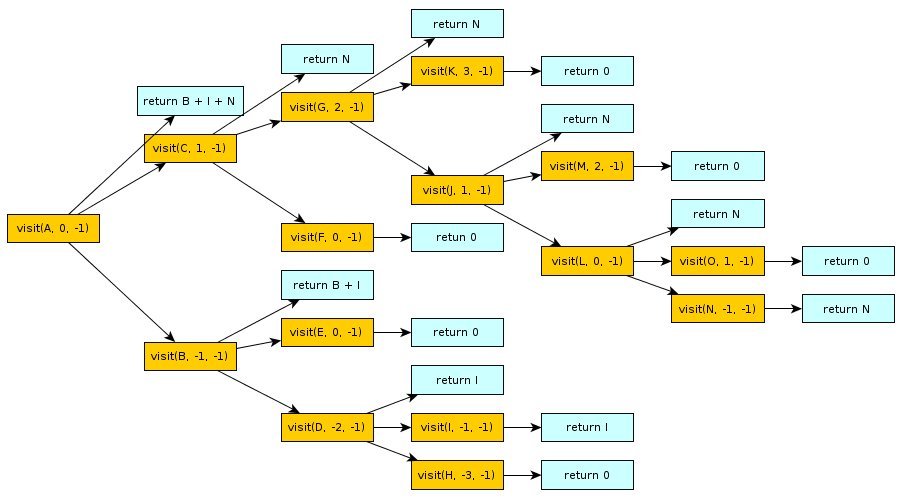
Следовательно visit(A, 0, -1) = B + I + N как и ожидалось.
Сложность всегда равна O(n), где n - количество узлов в дереве, потому что мы посещаем все дерево с первым порядком глубины и обрабатываем каждый узел только один раз.
Если мы хотим вычислить сумму каждого столбца, мы можем использовать следующий алгоритм
procedure visit(node n, int c) {
if (n.left != null)
S{c} += n.value;
visit(n.left, c - 1)
visit(n.right, c + 1)
}
и позвоните один раз visit(A, 0), где A является корневым узлом. Обратите внимание, что S{...} в алгоритме есть карта, ключами которой являются номера столбцов (..., -2, -1, 0, 1, 2, ...) и чьи значения (в конце алгоритма) являются суммами значений узлов в этом столбце (S{1} будет сумма узлов в столбце 1). Мы также можем использовать массив вместо карты при условии, что мы обращаем внимание на индексы (у массивов нет отрицательных индексов). Алгоритм все еще O(n), потому что мы проходим по всему дереву только один раз. Однако в этом случае нам нужно дополнительное место для хранения суммы для всех столбцов (карты или массива). Если я не ошибаюсь бинарное дерево высоты h буду иметь 2*h + 1 колонны.
public class Solution {
public static int getSum(BinaryTreeNode<Integer> root) {
//Your code goes here.
if(root==null){
return 0;
}
int leftnodesum=getSum(root.left);
int rightnodesum=getSum(root.right);
return root.data+leftnodesum+rightnodesum;
}
}
Как насчет следующего? (Внутри вашего класса узла предполагается, что getData возвращает целочисленное значение, hasRight() и hasLeft() являются логическими значениями, указывающими, существует ли правая / левая ветвь, а getRight() и getLeft() возвращают следующий узел в правой / левой ветке.
public int calculateVerticalLine(int numLine) {
return calculateVerticalLineRecursive(numLine, 0);
}
protected int calculateVerticalLineRecursive(int numLine, int curPosition) {
int result = 0;
if(numLine == curPosition) result += this.getData();
if(hasRight()) result += getRight().calculateVerticalLineRecursive(numLine, curPosition+1);
if(hasLeft()) result += getLeft().calculateVerticalLineRecursive(numLine, curPosition-1);
return result;
}