AVX2 Какой самый эффективный способ упаковать левый на основе маски?
Если у вас есть входной массив и выходной массив, но вы хотите записать только те элементы, которые удовлетворяют определенному условию, какой самый эффективный способ сделать это в AVX2?
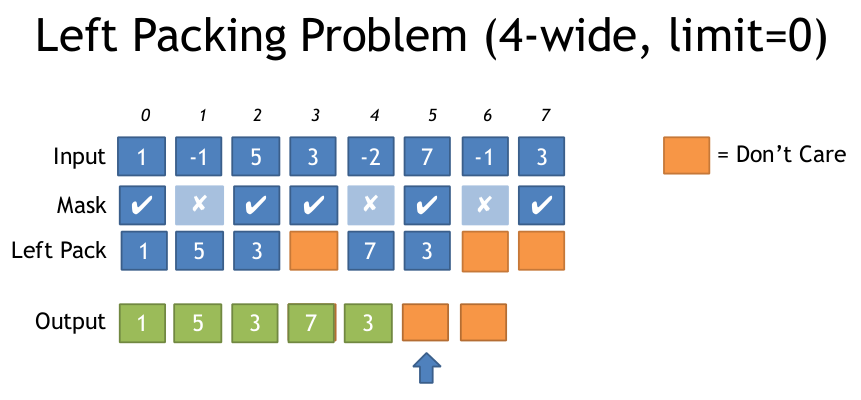
Я видел в SSE, где это было сделано так: (От: https://deplinenoise.files.wordpress.com/2015/03/gdc2015_afredriksson_simd.pdf)
__m128i LeftPack_SSSE3(__m128 mask, __m128 val)
{
// Move 4 sign bits of mask to 4-bit integer value.
int mask = _mm_movemask_ps(mask);
// Select shuffle control data
__m128i shuf_ctrl = _mm_load_si128(&shufmasks[mask]);
// Permute to move valid values to front of SIMD register
__m128i packed = _mm_shuffle_epi8(_mm_castps_si128(val), shuf_ctrl);
return packed;
}
Это кажется нормальным для SSE, который имеет ширину 4, и, следовательно, нуждается только в LUT с 16 входами, но для AVX, который имеет ширину 8, LUT становится довольно большим (256 записей, каждые 32 байта или 8 КБ).
Я удивлен, что у AVX нет инструкции по упрощению этого процесса, например, в магазине с маской и упаковкой.
Я думаю, что, посмотрев немного числа для подсчета числа # битов знака, установленных слева, вы можете сгенерировать необходимую таблицу перестановок и затем вызвать _mm256_permutevar8x32_ps. Но это тоже довольно много инструкций, я думаю..
Кто-нибудь знает какие-нибудь хитрости, чтобы сделать это с AVX2? Или какой самый эффективный метод?
Вот иллюстрация проблемы левой упаковки из вышеприведенного документа:
Спасибо
6 ответов
AVX2 + BMI2. Смотрите мой другой ответ для AVX512. (Обновление: сохранено pdep в 64-битных билдах.)
Мы можем использовать AVX2 vpermps ( _mm256_permutevar8x32_ps ) (или целочисленный эквивалент, vpermd) сделать перестановку по полосе.
Мы можем генерировать маски на лету, так как BMI2 pext (Извлечение параллельных битов) предоставляет нам побитовую версию нужной нам операции.
Для целочисленных векторов с 32-битными или более широкими элементами: либо 1) _mm256_movemask_ps(_mm256_castsi256_ps(compare_mask)),
Или 2) использовать _mm256_movemask_epi8 и затем измените первую константу PDEP с 0x0101010101010101 на 0x0F0F0F0F0F0F0F0F, чтобы разбросать блоки из 4 смежных битов. Измените умножение на 0xFFU на expanded_mask |= expanded_mask<<4; или же expanded_mask *= 0x11; (Не испытано). В любом случае, используйте маску тасования с VPERMD вместо VPERMPS.
Для 64-битного целого или double элементы, все еще просто работает; Просто в маске сравнения всегда есть пары одинаковых 32-битных элементов, поэтому в результате перемешивания обе половинки каждого 64-битного элемента размещаются в нужном месте. (Таким образом, вы все еще используете VPERMPS или VPERMD, потому что VPERMPD и VPERMQ доступны только с операндами непосредственного управления.)
Алгоритм:
Начните с константы упакованных 3-битных индексов, где каждая позиция имеет свой собственный индекс. т.е. [ 7 6 5 4 3 2 1 0 ] где каждый элемент имеет ширину 3 бита. 0b111'110'101'...'010'001'000,
использование pext чтобы извлечь нужные нам индексы в непрерывную последовательность внизу целочисленного регистра. например, если мы хотим индексы 0 и 2, наша контрольная маска для pext должно быть 0b000'...'111'000'111, pext возьму 010 а также 000 индексные группы, которые совпадают с 1 битом в селекторе. Выбранные группы упаковываются в младшие биты вывода, поэтому вывод будет 0b000'...'010'000, (т.е. [ ... 2 0 ])
Смотрите закомментированный код о том, как создать 0b111000111 вход для pext из входной векторной маски.
Теперь мы находимся в одной лодке со сжатым LUT: распаковываем до 8 упакованных индексов.
К тому времени, когда вы сложите все pext / pdeps. Я работал в обратном направлении от того, что я хотел, так что, вероятно, легче всего понять это и в этом направлении. (то есть начните с линии тасования и оттуда работайте задом наперед.)
Мы можем упростить распаковку, если будем работать с индексами по одному на байт вместо упакованных 3-битных групп. Поскольку у нас есть 8 индексов, это возможно только с 64-битным кодом.
Смотрите эту и 32-битную версию в Godbolt Compiler Explorer. я использовал #ifdef S так что он оптимально компилируется с -m64 или же -m32, GCC тратит некоторые инструкции, но Clang делает действительно хороший код.
#include <stdint.h>
#include <immintrin.h>
// Uses 64bit pdep / pext to save a step in unpacking.
__m256 compress256(__m256 src, unsigned int mask /* from movmskps */)
{
uint64_t expanded_mask = _pdep_u64(mask, 0x0101010101010101); // unpack each bit to a byte
expanded_mask *= 0xFF; // mask |= mask<<1 | mask<<2 | ... | mask<<7;
// ABC... -> AAAAAAAABBBBBBBBCCCCCCCC...: replicate each bit to fill its byte
const uint64_t identity_indices = 0x0706050403020100; // the identity shuffle for vpermps, packed to one index per byte
uint64_t wanted_indices = _pext_u64(identity_indices, expanded_mask);
__m128i bytevec = _mm_cvtsi64_si128(wanted_indices);
__m256i shufmask = _mm256_cvtepu8_epi32(bytevec);
return _mm256_permutevar8x32_ps(src, shufmask);
}
Это компилируется в код без нагрузки из памяти, только непосредственные константы. (См. Ссылку Godbolt для этого и 32-битной версии).
# clang 3.7.1 -std=gnu++14 -O3 -march=haswell
mov eax, edi # just to zero extend: goes away when inlining
movabs rcx, 72340172838076673 # The constants are hoisted after inlining into a loop
pdep rax, rax, rcx # ABC -> 0000000A0000000B....
imul rax, rax, 255 # 0000000A0000000B.. -> AAAAAAAABBBBBBBB..
movabs rcx, 506097522914230528
pext rax, rcx, rax
vmovq xmm1, rax
vpmovzxbd ymm1, xmm1 # 3c latency since this is lane-crossing
vpermps ymm0, ymm1, ymm0
ret
Так, согласно числам Агнера Фога, это 6 мопов (не считая констант, или расширяющегося нулями mov, который исчезает, когда встроен). В Intel Haswell это задержка 16c (1 для vmovq, 3 для каждого pdep/imul/pext / vpmovzx / vpermps). Там нет параллелизма на уровне инструкций. Однако в цикле, где это не является частью переносимой в цикле зависимости (подобно тому, который я включил в ссылку Godbolt), узкое место, как мы надеемся, просто пропускная способность, сохраняя несколько итераций этого в полете одновременно.
Это может быть возможно для управления пропускной способностью один на 3 цикла, узкое место на порту 1 для pdep/pext/imul. Конечно, с нагрузками / хранилищами и издержками цикла (включая сравнение, movmsk и popcnt), общая пропускная способность UOP может легко стать проблемой. (например, цикл фильтра в моей ссылке Godbolt - 14 моп с Clang, с -fno-unroll-loops чтобы было легче читать. Он может выдержать одну итерацию на 4c, не отставая от внешнего интерфейса, если нам повезет, но я думаю, что clang не смог объяснить popcnt Это ложная зависимость от его выхода, поэтому он будет узким местом на 3/5 от задержки compress256 функция).
gcc умножает на 0xFF с несколькими инструкциями, используя сдвиг влево на 8 и sub, Это требует дополнительного mov инструкции, но конечным результатом является умножение с задержкой 2. (Haswell обрабатывает mov на этапе регистрации-переименования с нулевой задержкой.)
Поскольку все оборудование, поддерживающее AVX2, также поддерживает BMI2, возможно, нет смысла предоставлять версию для AVX2 без BMI2.
Если вам нужно сделать это в очень длинном цикле, LUT, вероятно, того стоит, если начальные промахи кэша амортизируются в течение достаточного количества итераций с меньшими накладными расходами на простую распаковку записи LUT. Вам все еще нужно movmskps, так что вы можете открыть маску и использовать ее в качестве индекса LUT, но вы сохраните pdep/imul/pexp.
Вы можете распаковать записи LUT с той же последовательностью целых чисел, которую я использовал, но @ Froglegs's set1() / vpsrlvd / vpand Вероятно, это лучше, когда запись LUT начинается в памяти и не нуждается в целочисленных регистрах. (32-битная широковещательная загрузка не требует ALU-моп на процессорах Intel). Однако переменное смещение составляет 3 мопа на Haswell (но только 1 на Skylake).
Смотрите мой другой ответ для AVX2+BMI2 без LUT.
Поскольку вы упоминаете о проблеме масштабируемости для AVX512: не волнуйтесь, есть инструкция AVX512F именно для этого:
VCOMPRESSPS - Храните разреженные упакованные значения с плавающей запятой одинарной точности в плотной памяти. (Существуют также версии для двойных и 32- или 64-битных целочисленных элементов (vpcompressq), но не байт или слово (16 бит)). Это как BMI2 pdep / pext, но для векторов вместо битов в целочисленной рег.
Пункт назначения может быть векторным регистром или операндом памяти, а источником является вектор и регистр маски. С регистром dest он может объединять или обнулять старшие биты. С помощью dest назначения памяти "Только место смежного вектора записывается в ячейку памяти назначения".
Чтобы выяснить, как далеко продвинется указатель на следующий вектор, попкорн маску.
Допустим, вы хотите отфильтровать все, кроме значений>= 0 из массива:
#include <stdint.h>
#include <immintrin.h>
size_t filter_non_negative(float *__restrict__ dst, const float *__restrict__ src, size_t len) {
const float *endp = src+len;
float *dst_start = dst;
do {
__m512 sv = _mm512_loadu_ps(src);
__mmask16 keep = _mm512_cmp_ps_mask(sv, _mm512_setzero_ps(), _CMP_GE_OQ); // true for src >= 0.0, false for unordered and src < 0.0
_mm512_mask_compressstoreu_ps(dst, keep, sv); // clang is missing this intrinsic, which can't be emulated with a separate store
src += 16;
dst += _mm_popcnt_u64(keep); // popcnt_u64 instead of u32 helps gcc avoid a wasted movsx, but is potentially slower on some CPUs
} while (src < endp);
return dst - dst_start;
}
Это компилируется (с gcc4.9 или новее) в ( Godbolt Compiler Explorer):
# Output from gcc6.1, with -O3 -march=haswell -mavx512f. Same with other gcc versions
lea rcx, [rsi+rdx*4] # endp
mov rax, rdi
vpxord zmm1, zmm1, zmm1 # vpxor xmm1, xmm1,xmm1 would save a byte, using VEX instead of EVEX
.L2:
vmovups zmm0, ZMMWORD PTR [rsi]
add rsi, 64
vcmpps k1, zmm0, zmm1, 29 # AVX512 compares have mask regs as a destination
kmovw edx, k1 # There are some insns to add/or/and mask regs, but not popcnt
movzx edx, dx # gcc is dumb and doesn't know that kmovw already zero-extends to fill the destination.
vcompressps ZMMWORD PTR [rax]{k1}, zmm0
popcnt rdx, rdx
## movsx rdx, edx # with _popcnt_u32, gcc is dumb. No casting can get gcc to do anything but sign-extend. You'd expect (unsigned) would mov to zero-extend, but no.
lea rax, [rax+rdx*4] # dst += ...
cmp rcx, rsi
ja .L2
sub rax, rdi
sar rax, 2 # address math -> element count
ret
Я придумал этот метод, который использует сжатый LUT, который составляет 768(+1 заполнение) байтов вместо 8k. Это требует широковещательной передачи одного скалярного значения, которое затем сдвигается на разную величину в каждой полосе, а затем маскируется на младшие 3 бита, что обеспечивает 0-7 LUT.
Вот внутренняя версия, а также код для построения LUT.
//Generate Move mask via: _mm256_movemask_ps(_mm256_castsi256_ps(mask)); etc
__m256i MoveMaskToIndices(int moveMask) {
u8 *adr = g_pack_left_table_u8x3 + moveMask * 3;
__m256i indices = _mm256_set1_epi32(*reinterpret_cast<u32*>(adr));//lower 24 bits has our LUT
__m256i m = _mm256_sllv_epi32(indices, _mm256_setr_epi32(29, 26, 23, 20, 17, 14, 11, 8));
//now shift it right to get 3 bits at bottom
__m256i shufmask = _mm256_srli_epi32(m, 29);
return shufmask;
}
u32 get_nth_bits(int a) {
u32 out = 0;
int c = 0;
for (int i = 0; i < 8; ++i) {
auto set = (a >> i) & 1;
if (set) {
out |= (i << (c * 3));
c++;
}
}
return out;
}
u8 g_pack_left_table_u8x3[256 * 3 + 1];
void BuildPackMask() {
for (int i = 0; i < 256; ++i) {
*reinterpret_cast<u32*>(&g_pack_left_table_u8x3[i * 3]) = get_nth_bits(i);
}
}
Вот сборка, сгенерированная VS2015:
lea eax, DWORD PTR [rcx+rcx*2]
movsxd rcx, eax
lea rax, OFFSET FLAT:?g_pack_left_table_u8x3@@3PAEA ; g_pack_left_table_u8x3
vpbroadcastd ymm0, DWORD PTR [rcx+rax]
vpsllvd ymm0, ymm0, YMMWORD PTR __ymm@000000080000000b0000000e0000001100000014000000170000001a0000001d
vpsrld ymm0, ymm0, 29
Добавлю дополнительную информацию к отличному ответу от @PeterCordes: /questions/22715326/avx2-kakoj-samyij-effektivnyij-sposob-upakovat-levyij-na-osnove-maski/22715332#22715332.
С его помощью я реализовал std::remove из стандарта C++ для целочисленных типов. Как только вы сможете сжать, алгоритм относительно прост: загрузить регистр, сжать, сохранить. Сначала я покажу варианты, а затем тесты.
В итоге я получил два значимых варианта предлагаемого решения:
__m128iрегистры, любой тип элемента, используя_mm_shuffle_epi8инструкция__m256iрегистры, тип элемента не менее 4 байтов, используя_mm256_permutevar8x32_epi32
Когда типы меньше 4 байтов для 256-битного регистра, я разделяю их на два 128-битных регистра и сжимаю / сохраняю каждый отдельно.
Ссылка на обозреватель компилятора, где можно увидеть полную сборку (есть using type а также width(в элементах на упаковку) внизу, которые вы можете подключить, чтобы получить разные варианты): https://gcc.godbolt.org/z/yQFR2t
ПРИМЕЧАНИЕ: мой код находится на C++17 и использует настраиваемый simd обертки, поэтому я не знаю, насколько это читаемо. Если вы хотите прочитать мой код -> большая его часть находится за ссылкой вверху, включите Godbolt. В качестве альтернативы весь код находится на github.
Реализации @PeterCordes отвечают в обоих случаях
Примечание: вместе с маской я также вычисляю количество оставшихся элементов с помощью popcount. Может есть случай, когда он не нужен, но я его еще не видел.
Маска для _mm_shuffle_epi8
- Запишите индекс для каждого байта в полубайт:
0xfedcba9876543210 - Получите пары индексов в 8 коротких статей, упакованных в
__m128i - Распространите их, используя
x << 4 | x & 0x0f0f
Пример распространения индексов. Допустим, выбраны 7-й и 6-й элементы. Это означает, что соответствующий шорт будет:0x00fe. После<< 4 а также | мы бы получили 0x0ffe. А потом убираем второйf.
Полный код маски:
// helper namespace
namespace _compress_mask {
// mmask - result of `_mm_movemask_epi8`,
// `uint16_t` - there are at most 16 bits with values for __m128i.
inline std::pair<__m128i, std::uint8_t> mask128(std::uint16_t mmask) {
const std::uint64_t mmask_expanded = _pdep_u64(mmask, 0x1111111111111111) * 0xf;
const std::uint8_t offset =
static_cast<std::uint8_t>(_mm_popcnt_u32(mmask)); // To compute how many elements were selected
const std::uint64_t compressed_idxes =
_pext_u64(0xfedcba9876543210, mmask_expanded); // Do the @PeterCordes answer
const __m128i as_lower_8byte = _mm_cvtsi64_si128(compressed_idxes); // 0...0|compressed_indexes
const __m128i as_16bit = _mm_cvtepu8_epi16(as_lower_8byte); // From bytes to shorts over the whole register
const __m128i shift_by_4 = _mm_slli_epi16(as_16bit, 4); // x << 4
const __m128i combined = _mm_or_si128(shift_by_4, as_16bit); // | x
const __m128i filter = _mm_set1_epi16(0x0f0f); // 0x0f0f
const __m128i res = _mm_and_si128(combined, filter); // & 0x0f0f
return {res, offset};
}
} // namespace _compress_mask
template <typename T>
std::pair<__m128i, std::uint8_t> compress_mask_for_shuffle_epi8(std::uint32_t mmask) {
auto res = _compress_mask::mask128(mmask);
res.second /= sizeof(T); // bit count to element count
return res;
}
Маска для _mm256_permutevar8x32_epi32
Это почти одно решение @PeterCordes - единственная разница в том, _pdep_u64 бит (он предлагает это в качестве примечания).
Маска, которую я выбрала, 0x5555'5555'5555'5555. Идея такая: у меня 32 бита mmask, по 4 бита на каждое из 8 целых чисел. У меня есть 64 бита, которые я хочу получить => Мне нужно преобразовать каждый 32-битный бит в 2 => поэтому 0101b = 5. Множитель также меняется с 0xff на 3, потому что я получу 0x55 для каждого целого числа, а не 1.
Полный код маски:
// helper namespace
namespace _compress_mask {
// mmask - result of _mm256_movemask_epi8
inline std::pair<__m256i, std::uint8_t> mask256_epi32(std::uint32_t mmask) {
const std::uint64_t mmask_expanded = _pdep_u64(mmask, 0x5555'5555'5555'5555) * 3;
const std::uint8_t offset = static_cast<std::uint8_t(_mm_popcnt_u32(mmask)); // To compute how many elements were selected
const std::uint64_t compressed_idxes = _pext_u64(0x0706050403020100, mmask_expanded); // Do the @PeterCordes answer
// Every index was one byte => we need to make them into 4 bytes
const __m128i as_lower_8byte = _mm_cvtsi64_si128(compressed_idxes); // 0000|compressed indexes
const __m256i expanded = _mm256_cvtepu8_epi32(as_lower_8byte); // spread them out
return {expanded, offset};
}
} // namespace _compress_mask
template <typename T>
std::pair<__m256i, std::uint8_t> compress_mask_for_permutevar8x32(std::uint32_t mmask) {
static_assert(sizeof(T) >= 4); // You cannot permute shorts/chars with this.
auto res = _compress_mask::mask256_epi32(mmask);
res.second /= sizeof(T); // bit count to element count
return res;
}
Контрольные точки
Процессор: Intel Core i7 9700K (современный ЦП потребительского уровня, без поддержки AVX-512)
Компилятор: clang, сборка из ствола рядом с выпуском версии 10 Параметры
компилятора:--std=c++17 --stdlib=libc++ -g -Werror -Wall -Wextra -Wpedantic -O3 -march=native -mllvm -align-all-functions=7
Библиотека микротестирования: тест Google
Контроль выравнивания кода:
если вы не знакомы с концепцией, прочтите это или посмотрите это.
Все функции в бинарном тесте выровнены по границе 128 байт. Каждая функция тестирования дублируется 64 раза, с другим слайдом в начале функции (перед входом в цикл). Основные цифры, которые я показываю, - это минимальные значения для каждого измерения. Я думаю, что это работает, поскольку алгоритм встроен. Меня также подтверждает тот факт, что я получаю очень разные результаты. В самом низу ответа я показываю влияние выравнивания кода.
Примечание: тестовый код. BENCH_DECL_ATTRIBUTES - это просто noinline
Бенчмарк удаляет некоторый процент нулей из массива. Я тестирую массивы с {0, 5, 20, 50, 80, 95, 100} процентами нулей.
Я тестирую 3 размера: 40 байт (чтобы увидеть, можно ли его использовать для действительно маленьких массивов), 1000 байт и 10 000 байт. Я группирую по размеру, потому что SIMD зависит от размера данных, а не от количества элементов. Количество элементов может быть получено из размера элемента (1000 байтов - это 1000 символов, но 500 коротких и 250 целых чисел). Поскольку время, необходимое для кода, отличного от simd, зависит в основном от количества элементов, выигрыши должны быть больше для символов.
Графики: x - процент нулей, y - время в наносекундах. padding: min указывает, что это минимум среди всех выравниваний.
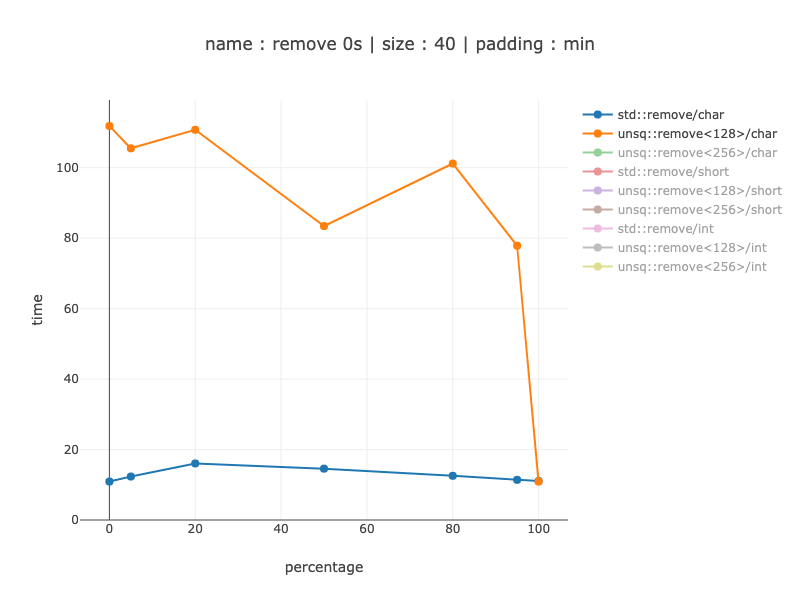
40 байт данных, 40 символов
Для 40 байт это не имеет смысла даже для символов - моя реализация становится примерно в 8-10 раз медленнее при использовании 128-битных регистров вместо кода, отличного от simd. Так, например, компилятор должен быть осторожен при этом.
1000 байт данных, 1000 символов
По-видимому, в версии без simd преобладает предсказание ветвлений: когда мы получаем небольшое количество нулей, мы получаем меньшую скорость: без нулей - примерно в 3 раза, для 5% нулей - примерно в 5-6 раз. Когда предсказатель ветвления не может помочь в версии, отличной от simd, скорость увеличивается примерно в 27 раз. Это интересное свойство simd-кода, что его производительность гораздо меньше зависит от данных. Использование 128 и 256 регистров практически не показывает разницы, поскольку большая часть работы по-прежнему разделена на 2 128 регистров.
1000 байтов данных, 500 коротких
Аналогичные результаты для шорт, только с гораздо меньшим приростом - до 2 раз. Я не знаю, почему шорты работают намного лучше, чем символы для кода, отличного от simd: я бы ожидал, что шорты будут в два раза быстрее, поскольку их всего 500, но на самом деле разница до 10 раз.
1000 байт данных, 250 int
Для 1000 имеет смысл только 256-битная версия - выигрыш 20-30%, исключая отсутствие нулей для удаления того, что когда-либо было (идеальное предсказание ветвления, без удаления для кода, отличного от simd).
10'000 байт данных, 10'000 символов
Выигрывает тот же порядок величины, что и для 1000 символов: от 2-6 раз быстрее, когда предсказатель ветвления полезен, до 27 раз, когда это не так.
Те же графики, только версии simd:
Здесь мы видим примерно 10% выигрыш от использования 256-битных регистров и разделения их на 2 128-битных: примерно на 10% быстрее. По размеру он увеличивается с 88 до 129 инструкций, что немного, поэтому может иметь смысл в зависимости от вашего сценария использования. Для базовой версии - не-simd-версия - это 79 инструкций (насколько я знаю - они меньше, чем SIMD).
10'000 байтов данных, 5'000 шорт
Выигрыш от 20% до 9 раз, в зависимости от распределения данных. Не показывать сравнение 256-битных и 128-битных регистров - это почти такая же сборка, что и для символов, и тот же выигрыш для 256-битных примерно 10%.
10'000 байтов данных, 2'500 целых
Кажется, имеет смысл использовать 256-битные регистры, эта версия примерно в 2 раза быстрее, чем 128-битные регистры. При сравнении с кодом non-simd - от 20% выигрыша при идеальном предсказании ветвления до 3,5 - 4 раза, если это не так.
Вывод: когда у вас есть достаточный объем данных (не менее 1000 байт), это может быть очень полезной оптимизацией для современного процессора без AVX-512.
PS:
Процент удаляемых элементов
С одной стороны, фильтровать половину элементов - это редкость. С другой стороны, аналогичный алгоритм может быть использован для разделения во время сортировки =>, который, как ожидается, будет иметь ~50% выбора ветвей.
Влияние выравнивания кода
Вопрос в том, сколько это будет стоить, если код окажется плохо выровненным (вообще говоря - с этим мало что можно поделать).
Я показываю только 10 000 байт.
На графиках есть две линии для минимума и максимума для каждой процентной точки (что означает - это не одно лучшее / худшее выравнивание кода - это лучшее выравнивание кода для данного процента).
Влияние выравнивания кода - non-simd
Символы:
От 15-20% для плохого предсказания ветвления до 2-3 раз, когда предсказание ветвления очень помогло. (известно, что на предсказатель ветвления влияет выравнивание кода).
Шорты:
Почему-то - 0 процентов вообще не влияет. Это можно объяснитьstd::removeсначала выполняется линейный поиск, чтобы найти первый удаляемый элемент. Видимо линейный поиск шорт не влияет. В остальном - от 10% до 1,6-1,8 раза больше.
Интс:
То же, что и для шорт - никакие нули не затрагиваются. Как только мы перейдем к удаленной части, она вырастет от 1,3 до 5 раз лучше, чем в лучшем случае.
Влияние выравнивания кода - версии simd
Не показывать шорты и целые 128, так как это почти такая же сборка, что и для символов
Chars - 128-битный регистр Примерно в 1,2 раза медленнее
Chars - регистр 256 бит Примерно в 1,1 - 1,24 раза медленнее
Ints - 256-битный регистр в
 1,25 - 1,35 раза медленнее
1,25 - 1,35 раза медленнее
Мы можем видеть, что для версии алгоритма simd выравнивание кода оказывает значительно меньшее влияние по сравнению с версией без simd. Подозреваю, что это из-за практически отсутствия филиалов.
В случае, если кто-то заинтересован, здесь есть решение для SSE2, которое использует инструкцию LUT вместо данных LUT или таблицы переходов. С AVX это потребовало бы 256 случаев все же.
Каждый раз, когда вы звоните LeftPack_SSE2 ниже он использует по существу три инструкции: jmp, shufps, jmp. В пяти из шестнадцати случаев нет необходимости изменять вектор.
static inline __m128 LeftPack_SSE2(__m128 val, int mask) {
switch(mask) {
case 0:
case 1: return val;
case 2: return _mm_shuffle_ps(val,val,0x01);
case 3: return val;
case 4: return _mm_shuffle_ps(val,val,0x02);
case 5: return _mm_shuffle_ps(val,val,0x08);
case 6: return _mm_shuffle_ps(val,val,0x09);
case 7: return val;
case 8: return _mm_shuffle_ps(val,val,0x03);
case 9: return _mm_shuffle_ps(val,val,0x0c);
case 10: return _mm_shuffle_ps(val,val,0x0d);
case 11: return _mm_shuffle_ps(val,val,0x34);
case 12: return _mm_shuffle_ps(val,val,0x0e);
case 13: return _mm_shuffle_ps(val,val,0x38);
case 14: return _mm_shuffle_ps(val,val,0x39);
case 15: return val;
}
}
__m128 foo(__m128 val, __m128 maskv) {
int mask = _mm_movemask_ps(maskv);
return LeftPack_SSE2(val, mask);
}
Возможно, это немного поздно, хотя я недавно столкнулся с этой конкретной проблемой и нашел альтернативное решение, в котором использовалась строго реализация AVX. Если вам все равно, заменяются ли распакованные элементы последними элементами каждого вектора, это тоже может сработать. Ниже представлена версия AVX:
inline __m128 left_pack(__m128 val, __m128i mask) noexcept
{
const __m128i shiftMask0 = _mm_shuffle_epi32(mask, 0xA4);
const __m128i shiftMask1 = _mm_shuffle_epi32(mask, 0x54);
const __m128i shiftMask2 = _mm_shuffle_epi32(mask, 0x00);
__m128 v = val;
v = _mm_blendv_ps(_mm_permute_ps(v, 0xF9), v, shiftMask0);
v = _mm_blendv_ps(_mm_permute_ps(v, 0xF9), v, shiftMask1);
v = _mm_blendv_ps(_mm_permute_ps(v, 0xF9), v, shiftMask2);
return v;
}
По сути, каждый элемент в
val сдвигается один раз влево с использованием битового поля,
0xF9для смешивания с несмещенным вариантом. Затем обе версии со сдвигом и без сдвига смешиваются с входной маской (которая имеет первый ненулевой элемент, транслируемый по остальным элементам 3 и 4). Повторите этот процесс еще два раза, транслируя второй и третий элементы
mask к его последующим элементам на каждой итерации, и это должно обеспечить версию AVX
_pdep_u32() Инструкция BMI2.
Если у вас нет AVX, вы можете легко поменять каждый
_mm_permute_ps() с
_mm_shuffle_ps() для версии, совместимой с SSE4.1.
А если вы используете двойную точность, вот дополнительная версия для AVX2:
inline __m256 left_pack(__m256d val, __m256i mask) noexcept
{
const __m256i shiftMask0 = _mm256_permute4x64_epi64(mask, 0xA4);
const __m256i shiftMask1 = _mm256_permute4x64_epi64(mask, 0x54);
const __m256i shiftMask2 = _mm256_permute4x64_epi64(mask, 0x00);
__m256d v = val;
v = _mm256_blendv_pd(_mm256_permute4x64_pd(v, 0xF9), v, shiftMask0);
v = _mm256_blendv_pd(_mm256_permute4x64_pd(v, 0xF9), v, shiftMask1);
v = _mm256_blendv_pd(_mm256_permute4x64_pd(v, 0xF9), v, shiftMask2);
return v;
}
Кроме того
_mm_popcount_u32(_mm_movemask_ps(val)) можно использовать для определения количества элементов, оставшихся после левой упаковки.