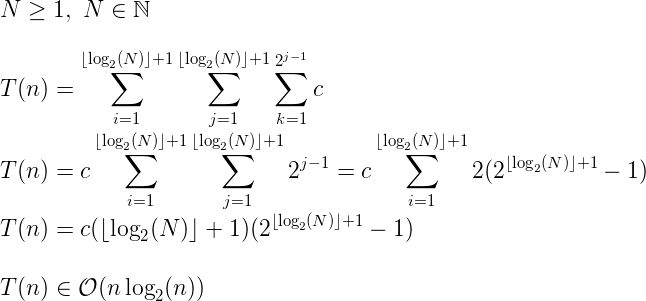Каков порядок роста наихудшего времени выполнения следующего фрагмента кода в зависимости от N?

int sum = 0;
for (int i = 1; i <= N; i = i*2)
    for (int j = 1; j <= N; j = j*2)
        for (int k = 1; k <= j; k++)
            sum++;

Согласно решению это NlogN. Однако я думал, что это будет просто логин. i цикл for повторяет logN раз, потому что я удваиваюсь с каждой итерацией. j цикл равен так же, как i цикл for, поэтому он повторяет logN раз. Наконец, k цикл for, потому что он установлен меньше или равен j, он будет повторяться столько же раз j делает и, таким образом, у нас есть еще итерации logN. Умножая эти три значения вместе, мы получаем logN * logN * logN полных итераций или (logN)^3 для сложности. Почему мой мыслительный процесс неверен?

Источник

2 ответа

Решение
sum++;

Это, очевидно, O(1)

for (int k = 1; k <= j; k++)
    sum++;

Петли бегут j раз, так что это O(j)

for (int j = 1; j <= N; j = j*2)
    for (int k = 1; k <= j; k++)
        sum++;

Так что это становится сложно. Мы знаем, что внутренний цикл O(j) но j меняется во внешнем цикле. Вы сказали:

Наконец, цикл k for, поскольку он установлен меньше или равен j, он будет повторять то же число раз, сколько j делает

№ j Цикл рассчитывается по двойникам. Но внутренний цикл отсчитывает с приращением. Они не пройдут одинаковое количество итераций.

Поскольку каждый внутренний цикл выполняется за время O(j), нам просто нужно сложить j для каждого времени в цикле. j удваивается каждый раз, так что это дает нам:

1 + 2 + 4 + 8 + 16 + ... + n

Эта последовательность оказывается чуть меньше 2n. (Почему это оставлено в качестве упражнения для читателя.) Таким образом, его O(n)

for (int i = 1; i <= N; i = i*2)
    for (int j = 1; j <= N; j = j*2)
        for (int k = 1; k <= j; k++)
            sum++;

Внешний цикл не взаимодействует с внутренними циклами, а работает log(N) раз дает нам O(N log N)

Источник

Используя сигма-нотацию, вы можете методически получить точную формулу:

Источник
Другие вопросы по тегам