Кластерный анализ в R: определить оптимальное количество кластеров
Будучи новичком в R, я не очень уверен, как выбрать лучшее количество кластеров для анализа k-средних. После построения подмножества данных ниже, сколько кластеров будет уместным? Как я могу выполнить кластерный анализ дендро?
n = 1000
kk = 10
x1 = runif(kk)
y1 = runif(kk)
z1 = runif(kk)
x4 = sample(x1,length(x1))
y4 = sample(y1,length(y1))
randObs <- function()
{
ix = sample( 1:length(x4), 1 )
iy = sample( 1:length(y4), 1 )
rx = rnorm( 1, x4[ix], runif(1)/8 )
ry = rnorm( 1, y4[ix], runif(1)/8 )
return( c(rx,ry) )
}
x = c()
y = c()
for ( k in 1:n )
{
rPair = randObs()
x = c( x, rPair[1] )
y = c( y, rPair[2] )
}
z <- rnorm(n)
d <- data.frame( x, y, z )
9 ответов
Если ваш вопрос how can I determine how many clusters are appropriate for a kmeans analysis of my data?Тогда вот несколько вариантов. Статья в Википедии об определении количества кластеров содержит хороший обзор некоторых из этих методов.
Во-первых, некоторые воспроизводимые данные (данные в Q... для меня неясны):
n = 100
g = 6
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))),
y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
plot(d)
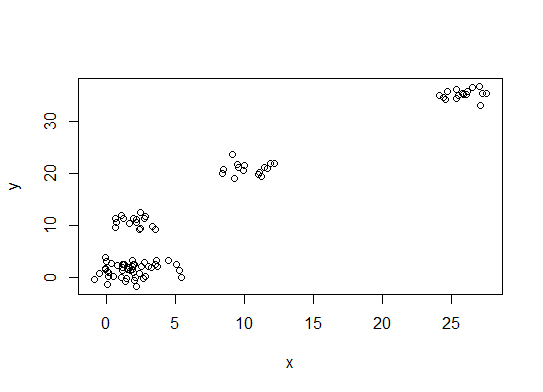
Один Ищите изгиб или колено на графике осциллограммы суммы квадратов ошибок (SSE). См. http://www.statmethods.net/advstats/cluster.html & http://www.mattpeeples.net/kmeans.html для получения дополнительной информации. Расположение колена на полученном графике предполагает подходящее количество кластеров для kmeans:
mydata <- d
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
for (i in 2:15) wss[i] <- sum(kmeans(mydata,
centers=i)$withinss)
plot(1:15, wss, type="b", xlab="Number of Clusters",
ylab="Within groups sum of squares")
Мы могли бы заключить, что 4 кластера будут обозначены этим методом: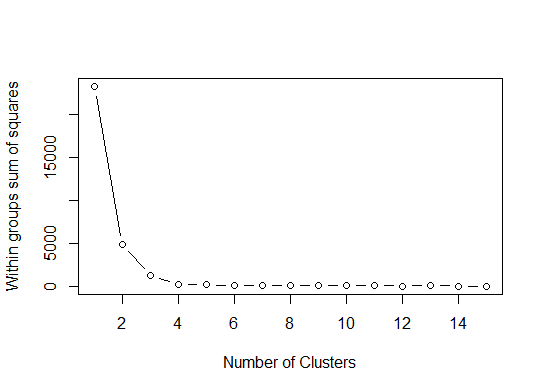
Два Вы можете разделить медоиды, чтобы оценить количество кластеров, используя pamk функция в пакете fpc.
library(fpc)
pamk.best <- pamk(d)
cat("number of clusters estimated by optimum average silhouette width:", pamk.best$nc, "\n")
plot(pam(d, pamk.best$nc))
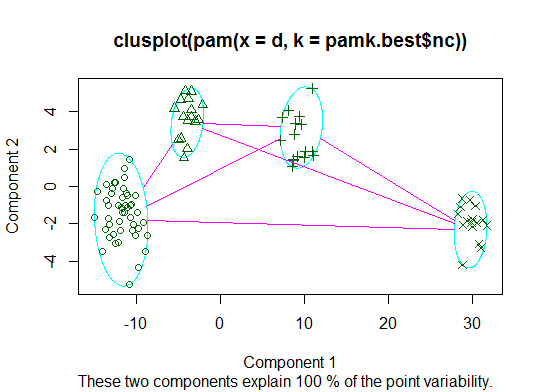
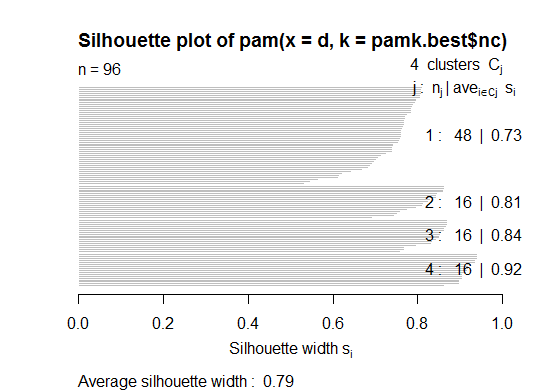
# we could also do:
library(fpc)
asw <- numeric(20)
for (k in 2:20)
asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
cat("silhouette-optimal number of clusters:", k.best, "\n")
# still 4
Три Критерий Калинского: еще один подход к диагностике того, сколько кластеров соответствует данным. В этом случае мы пробуем от 1 до 10 групп.
require(vegan)
fit <- cascadeKM(scale(d, center = TRUE, scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
cat("Calinski criterion optimal number of clusters:", calinski.best, "\n")
# 5 clusters!
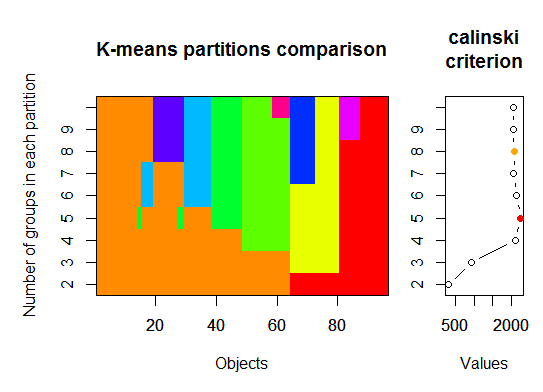
Четыре Определить оптимальную модель и количество кластеров согласно байесовскому информационному критерию для максимизации ожидания, инициализированному иерархической кластеризацией для параметризованных моделей гауссовой смеси
# See http://www.jstatsoft.org/v18/i06/paper
# http://www.stat.washington.edu/research/reports/2006/tr504.pdf
#
library(mclust)
# Run the function to see how many clusters
# it finds to be optimal, set it to search for
# at least 1 model and up 20.
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
cat("model-based optimal number of clusters:", m.best, "\n")
# 4 clusters
plot(d_clust)
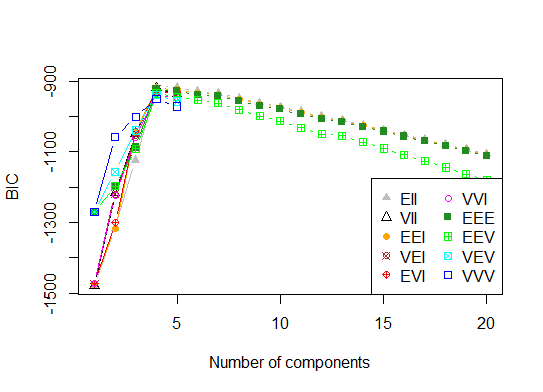
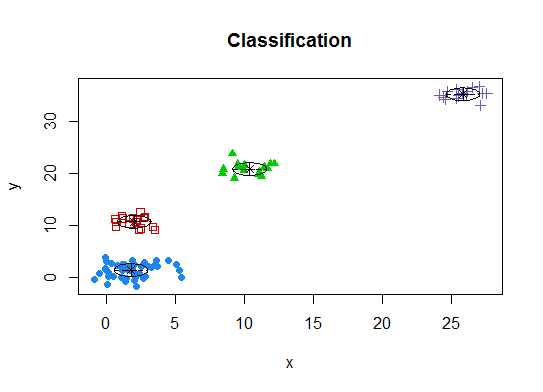
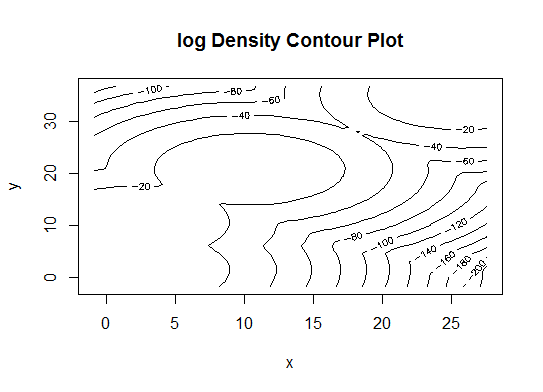
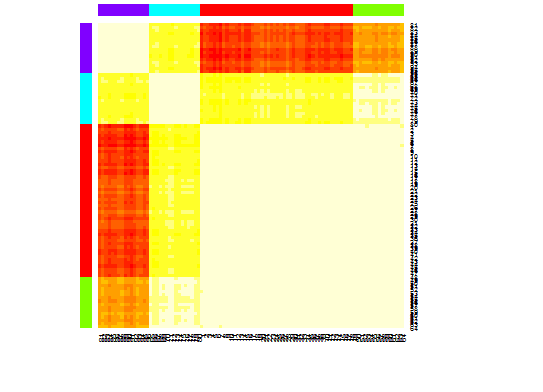
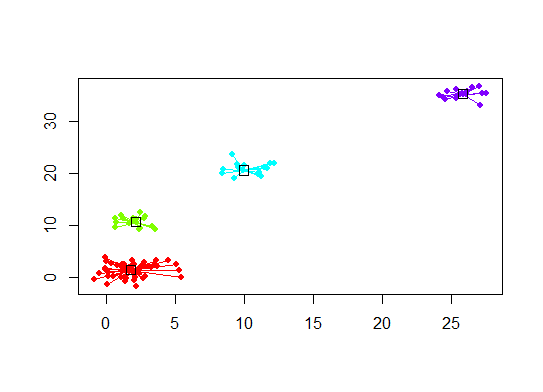
Пять Кластеризация распространения сродства (AP), см. http://dx.doi.org/10.1126/science.1136800
library(apcluster)
d.apclus <- apcluster(negDistMat(r=2), d)
cat("affinity propogation optimal number of clusters:", length(d.apclus@clusters), "\n")
# 4
heatmap(d.apclus)
plot(d.apclus, d)
Шесть Статистика зазора для оценки количества кластеров. Смотрите также некоторый код для хорошего графического вывода. Попытка 2-10 кластеров здесь:
library(cluster)
clusGap(d, kmeans, 10, B = 100, verbose = interactive())
Clustering k = 1,2,..., K.max (= 10): .. done
Bootstrapping, b = 1,2,..., B (= 100) [one "." per sample]:
.................................................. 50
.................................................. 100
Clustering Gap statistic ["clusGap"].
B=100 simulated reference sets, k = 1..10
--> Number of clusters (method 'firstSEmax', SE.factor=1): 4
logW E.logW gap SE.sim
[1,] 5.991701 5.970454 -0.0212471 0.04388506
[2,] 5.152666 5.367256 0.2145907 0.04057451
[3,] 4.557779 5.069601 0.5118225 0.03215540
[4,] 3.928959 4.880453 0.9514943 0.04630399
[5,] 3.789319 4.766903 0.9775842 0.04826191
[6,] 3.747539 4.670100 0.9225607 0.03898850
[7,] 3.582373 4.590136 1.0077628 0.04892236
[8,] 3.528791 4.509247 0.9804556 0.04701930
[9,] 3.442481 4.433200 0.9907197 0.04935647
[10,] 3.445291 4.369232 0.9239414 0.05055486
Вот результат реализации статистики разрыва Эдвином Ченом: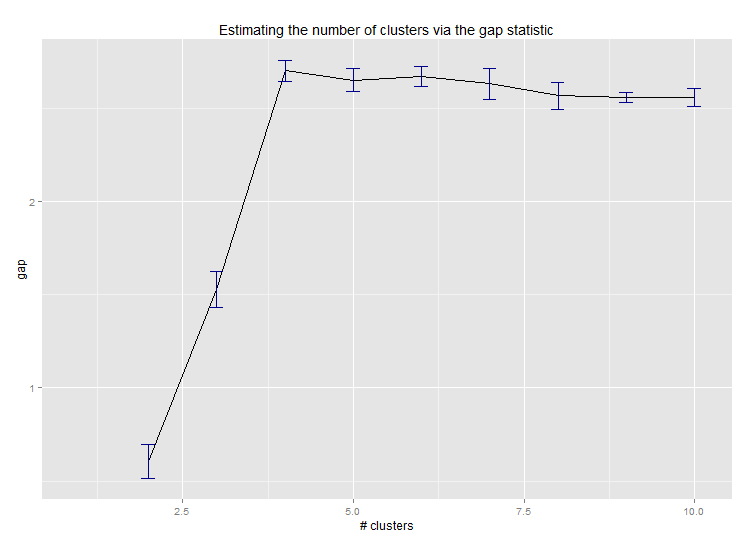
Семь Вам также может быть полезно изучить данные с помощью кластерных диаграмм для визуализации назначения кластеров, см. http://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/ для более подробной информации.
Восемь Пакет NbClust предоставляет 30 индексов для определения количества кластеров в наборе данных.
library(NbClust)
nb <- NbClust(d, diss="NULL", distance = "euclidean",
min.nc=2, max.nc=15, method = "kmeans",
index = "alllong", alphaBeale = 0.1)
hist(nb$Best.nc[1,], breaks = max(na.omit(nb$Best.nc[1,])))
# Looks like 3 is the most frequently determined number of clusters
# and curiously, four clusters is not in the output at all!
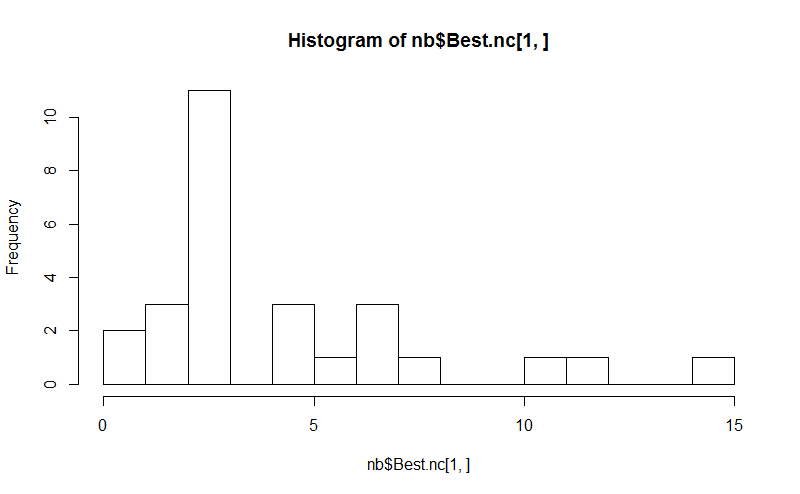
Если ваш вопрос how can I produce a dendrogram to visualize the results of my cluster analysis, тогда вы должны начать с этих: http://www.statmethods.net/advstats/cluster.html http://www.r-tutor.com/gpu-computing/clustering/hierarchical-cluster-analysis http://gastonsanchez.wordpress.com/2012/10/03/7-ways-to-plot-dendrograms-in-r/ И смотрите здесь для более экзотических методов: http://cran.r-project.org/web/views/Cluster.html
Вот несколько примеров:
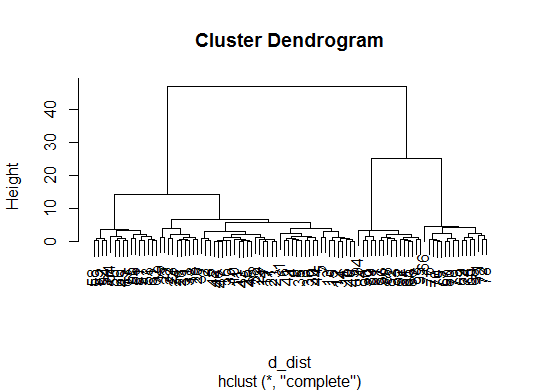
d_dist <- dist(as.matrix(d)) # find distance matrix
plot(hclust(d_dist)) # apply hirarchical clustering and plot
# a Bayesian clustering method, good for high-dimension data, more details:
# http://vahid.probstat.ca/paper/2012-bclust.pdf
install.packages("bclust")
library(bclust)
x <- as.matrix(d)
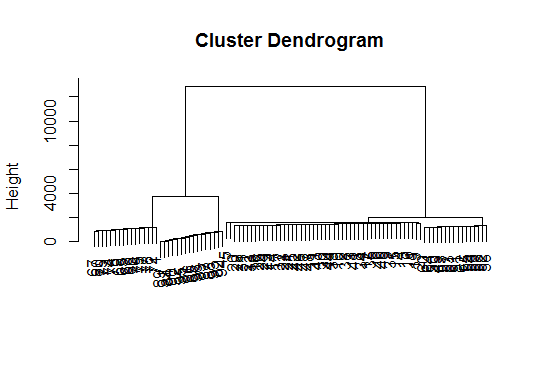
d.bclus <- bclust(x, transformed.par = c(0, -50, log(16), 0, 0, 0))
viplot(imp(d.bclus)$var); plot(d.bclus); ditplot(d.bclus)
dptplot(d.bclus, scale = 20, horizbar.plot = TRUE,varimp = imp(d.bclus)$var, horizbar.distance = 0, dendrogram.lwd = 2)
# I just include the dendrogram here
Также для данных большого размера pvclust библиотека, которая вычисляет p-значения для иерархической кластеризации с помощью мультимасштабной начальной загрузки. Вот пример из документации (не будет работать с такими низкоразмерными данными, как в моем примере):
library(pvclust)
library(MASS)
data(Boston)
boston.pv <- pvclust(Boston)
plot(boston.pv)
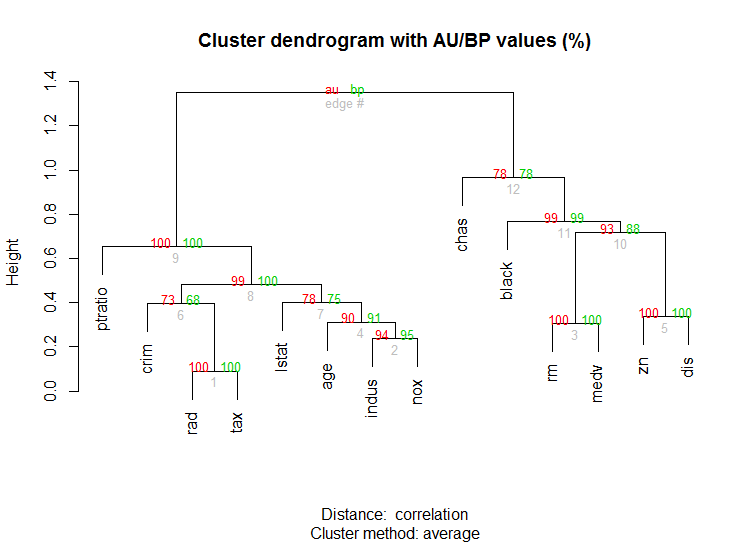
Помогает ли что-нибудь из этого?
Трудно добавить что-то слишком сложный ответ. Хотя я чувствую, что мы должны упомянуть identify здесь, особенно потому, что @Ben показывает множество примеров дендрограмм.
d_dist <- dist(as.matrix(d)) # find distance matrix
plot(hclust(d_dist))
clusters <- identify(hclust(d_dist))
identify позволяет вам интерактивно выбирать кластеры из дендрограммы и сохраняет ваши выборы в списке. Нажмите Esc, чтобы выйти из интерактивного режима и вернуться в консоль R. Обратите внимание, что список содержит индексы, а не имена строк (в отличие от cutree).
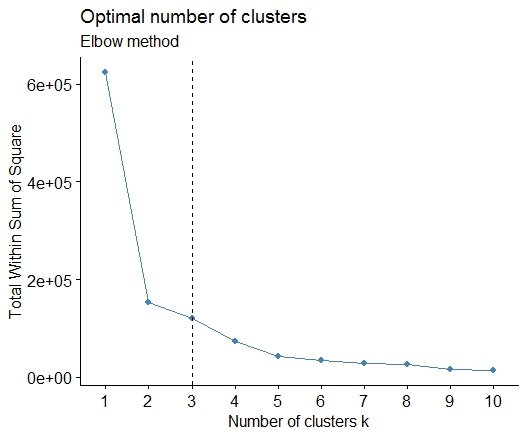
Для определения оптимального k-кластера в методах кластеризации. Я обычно использую Elbow метод сопровождается параллельной обработкой, чтобы избежать затрат времени. Этот код может привести пример:
Метод локтя
elbow.k <- function(mydata){
dist.obj <- dist(mydata)
hclust.obj <- hclust(dist.obj)
css.obj <- css.hclust(dist.obj,hclust.obj)
elbow.obj <- elbow.batch(css.obj)
k <- elbow.obj$k
return(k)
}
Бег Локоть параллельно
no_cores <- detectCores()
cl<-makeCluster(no_cores)
clusterEvalQ(cl, library(GMD))
clusterExport(cl, list("data.clustering", "data.convert", "elbow.k", "clustering.kmeans"))
start.time <- Sys.time()
elbow.k.handle(data.clustering))
k.clusters <- parSapply(cl, 1, function(x) elbow.k(data.clustering))
end.time <- Sys.time()
cat('Time to find k using Elbow method is',(end.time - start.time),'seconds with k value:', k.clusters)
Это работает хорошо.
Простое решение - библиотека factoextra, Вы можете изменить метод кластеризации и метод расчета лучшего количества групп. Например, если вы хотите узнать наилучшее количество кластеров для k-средних:
Данные: mtcars
library(factoextra)
fviz_nbclust(mtcars, kmeans, method = "wss") +
geom_vline(xintercept = 3, linetype = 2)+
labs(subtitle = "Elbow method")
Наконец, мы получаем график вроде:
Великолепный ответ от Бена. Однако я удивлен, что метод Affinity Propagation (AP) был предложен здесь только для того, чтобы найти номер кластера для метода k-средних, где в общем случае AP лучше выполняет кластеризацию данных. Пожалуйста, смотрите научную статью, поддерживающую этот метод в науке здесь:
Фрей, Брендан Дж. И Дельберт Дуек. "Кластеризация путем передачи сообщений между точками данных". Science 315.5814 (2007): 972-976.
Поэтому, если вы не склонны к k-средствам, я предлагаю использовать AP напрямую, что позволит кластеризовать данные без необходимости знать количество кластеров:
library(apcluster)
apclus = apcluster(negDistMat(r=2), data)
show(apclus)
Если отрицательные евклидовы расстояния не подходят, то вы можете использовать другие меры подобия, представленные в том же пакете. Например, для сходства, основанного на корреляциях Спирмена, это то, что вам нужно:
sim = corSimMat(data, method="spearman")
apclus = apcluster(s=sim)
Обратите внимание, что эти функции для сходства в пакете AP просто предоставлены для простоты. Фактически, функция apcluster() в R будет принимать любую матрицу корреляций. То же самое раньше с помощью corSimMat() можно сделать с помощью этого:
sim = cor(data, method="spearman")
или же
sim = cor(t(data), method="spearman")
в зависимости от того, что вы хотите кластеризовать на вашей матрице (строки или столбцы).
Эти методы хороши, но при попытке найти k для гораздо больших наборов данных, они могут быть очень медленными в R.
Хорошее решение, которое я нашел, - это пакет "RWeka", который имеет эффективную реализацию алгоритма X-Means - расширенную версию K-Means, которая лучше масштабируется и определит оптимальное количество кластеров для вас.
Сначала вы должны убедиться, что Weka установлена в вашей системе и что XMeans установлен через инструмент менеджера пакетов Weka.
library(RWeka)
# Print a list of available options for the X-Means algorithm
WOW("XMeans")
# Create a Weka_control object which will specify our parameters
weka_ctrl <- Weka_control(
I = 1000, # max no. of overall iterations
M = 1000, # max no. of iterations in the kMeans loop
L = 20, # min no. of clusters
H = 150, # max no. of clusters
D = "weka.core.EuclideanDistance", # distance metric Euclidean
C = 0.4, # cutoff factor ???
S = 12 # random number seed (for reproducibility)
)
# Run the algorithm on your data, d
x_means <- XMeans(d, control = weka_ctrl)
# Assign cluster IDs to original data set
d$xmeans.cluster <- x_means$class_ids
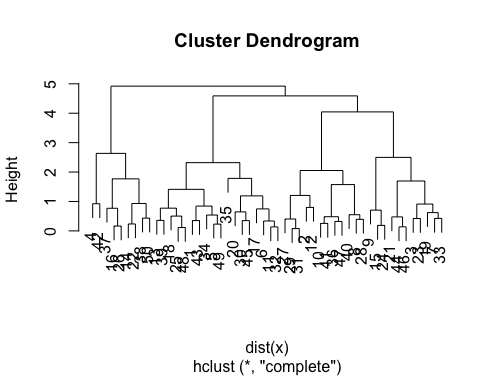
Ответы отличные. Если вы хотите дать шанс другому методу кластеризации, вы можете использовать иерархическую кластеризацию и посмотреть, как данные разделяются.
> set.seed(2)
> x=matrix(rnorm(50*2), ncol=2)
> hc.complete = hclust(dist(x), method="complete")
> plot(hc.complete)
В зависимости от того, сколько классов вам нужно, вы можете вырезать свою дендрограмму как;
> cutree(hc.complete,k = 2)
[1] 1 1 1 2 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1 1 2 1 1 1
[26] 2 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 2 1 1 1 1 1 1 1 2
Если вы печатаете ?cutree вы увидите определения. Если ваш набор данных имеет три класса, это будет просто cutree(hc.complete, k = 3), Эквивалент для cutree(hc.complete,k = 2) является cutree(hc.complete,h = 4.9),
Вам стоит посмотреть на NbClust. Он реализует более тридцати методов для определения оптимального количества кластеров,
Очень сложно просматривать такое количество функций без учета фактора производительности. Я понимаю, что немногие функции в доступных пакетах делают гораздо больше, чем просто находят оптимальное количество кластеров. Вот результаты тестов этих функций для тех, кто рассматривает эти функции для своего проекта -
n = 100
g = 6
set.seed(g)
d <- data.frame(x = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))),
y = unlist(lapply(1:g, function(i) rnorm(n/g, runif(1)*i^2))))
mydata <- d
require(cluster)
require(vegan)
require(mclust)
require(apcluster)
require(NbClust)
require(fpc)
microbenchmark::microbenchmark(
wss = {
wss <- (nrow(mydata)-1)*sum(apply(mydata,2,var))
for (i in 2:15) wss[i] <- sum(kmeans(mydata, centers=i)$withinss)
},
fpc = {
asw <- numeric(20)
for (k in 2:20)
asw[[k]] <- pam(d, k) $ silinfo $ avg.width
k.best <- which.max(asw)
},
fpc_1 = fpc::pamk(d),
vegan = {
fit <- cascadeKM(scale(d, center = TRUE, scale = TRUE), 1, 10, iter = 1000)
plot(fit, sortg = TRUE, grpmts.plot = TRUE)
calinski.best <- as.numeric(which.max(fit$results[2,]))
},
mclust = {
d_clust <- Mclust(as.matrix(d), G=1:20)
m.best <- dim(d_clust$z)[2]
},
d.apclus = apcluster(negDistMat(r=2), d),
clusGap = clusGap(d, kmeans, 10, B = 100, verbose = interactive()),
NbClust = NbClust(d, diss=NULL, distance = "euclidean",
method = "kmeans", min.nc=2, max.nc=15,
index = "alllong", alphaBeale = 0.1),
times = 1)
Unit: milliseconds
expr min lq mean median uq max neval
wss 16.83938 16.83938 16.83938 16.83938 16.83938 16.83938 1
fpc 221.99490 221.99490 221.99490 221.99490 221.99490 221.99490 1
fpc_1 43.10493 43.10493 43.10493 43.10493 43.10493 43.10493 1
vegan 1096.08568 1096.08568 1096.08568 1096.08568 1096.08568 1096.08568 1
mclust 1531.69475 1531.69475 1531.69475 1531.69475 1531.69475 1531.69475 1
d.apclus 28.56100 28.56100 28.56100 28.56100 28.56100 28.56100 1
clusGap 1096.50680 1096.50680 1096.50680 1096.50680 1096.50680 1096.50680 1
NbClust 10940.98807 10940.98807 10940.98807 10940.98807 10940.98807 10940.98807 1
Я нашел функцию
pamkв
fpcpackage, чтобы быть наиболее полезным для моих требований.