Накачка леммы в контекстно-свободных языках

Question

A = {0^a 1^b 2^c | a < b < c}

Мне нужно показать, что A не является контекстно-свободным. Я предполагаю, что для этого мне нужно использовать Лемму прокачки, но как?

Answer 1

Цель состоит в том, чтобы доказать, что для любой струны с длиной>= минимальной длины накачки, строка не может быть накачана. То есть если разбить его на подстроки uvxyzстрока, которая получается в результате создания копий (или удаления копий) v а также y все еще на языке A,

Обратите внимание, что вам нужно только показать, что одна строка на языке не может быть перекачена (при условии, что она соответствует минимальной длине перекачки p)

Рассмотрим этот язык и как он связан с A:

Answer 2

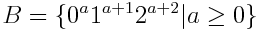
Шаг первый: определите минимальную длину прокачки (2^p+1), где p - количество переменных. Шаг второй: сделайте несколько строк такой длины. Шаг третий: начните разрезать строки в vwxyz так, чтобы | wy ​​|> 0 (заметьте, что |x| CAN может быть нулем) и |wxy| <= 2^p+1. Посмотрите, как можно определить w и y, и что произойдет, когда вы начнете повторять эти подстроки на месте.

Ключ, вероятно, будет находиться на разделительной линии между 0 и 1.