Как сгруппировать близлежащие местоположения широты и долготы, хранящиеся в SQL

Я пытаюсь проанализировать данные об авариях на велосипеде в Великобритании, чтобы найти статистические черные пятна. Вот пример данных с другого сайта. http://www.cycleinjury.co.uk/map

В настоящее время я использую SQLite для хранения 100 000 латов. Я хочу сгруппировать близлежащие места вместе. Эта задача называется кластерным анализом.

Я хотел бы упростить набор данных, игнорируя отдельные инциденты и вместо этого показывая только происхождение кластеров, в которых произошло несколько аварий на небольшой территории.

Есть 3 проблемы, которые мне нужно преодолеть.

  1. Производительность - Как мне быстро найти ближайшие точки? Должен ли я использовать реализацию R-дерева в SQLite, например?

  2. Цепи - Как мне избежать цепей соседних точек?

  3. Плотность - Как принять во внимание плотность населения цикла? В Лондоне гораздо более высокая плотность велосипедистов, чем, скажем, в Бристоле, поэтому в Лондоне, похоже, больше шансов на помощь.

Я хотел бы избежать "цепных" сценариев, подобных этому:

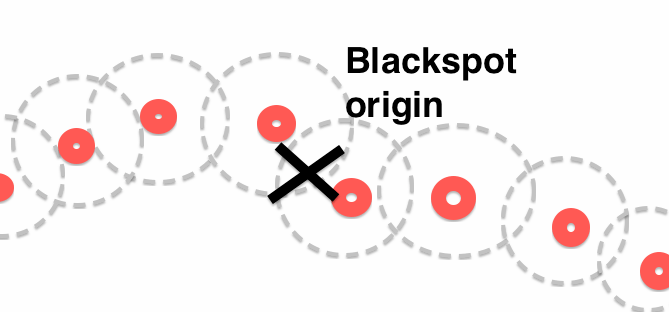
Вместо этого я хотел бы найти кластеры:

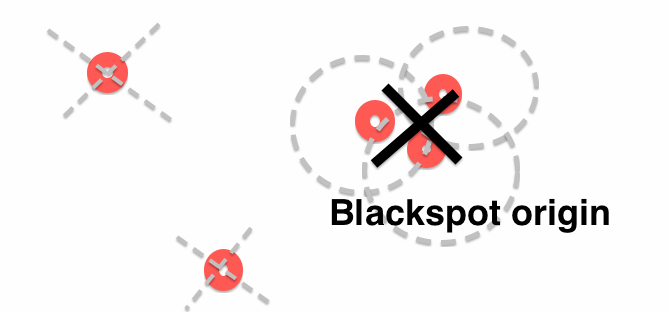
Скриншот Лондона (я нарисовал несколько кластеров)...

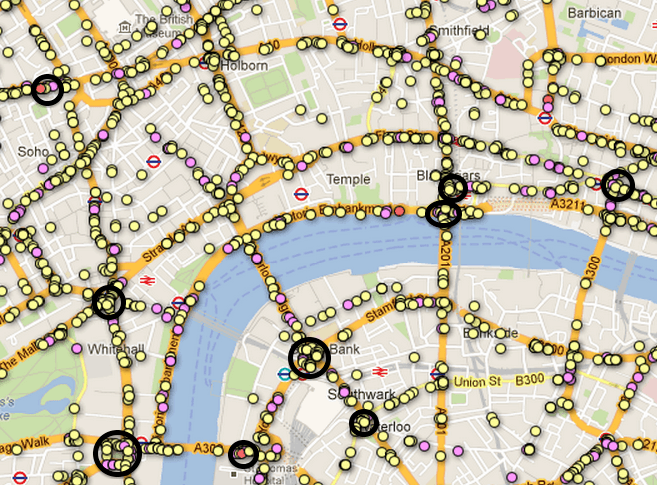
Бристольский скриншот - гораздо меньшая плотность - та же программа, запущенная над этой областью, может не найти черных пятен, если не учитывать относительную плотность.

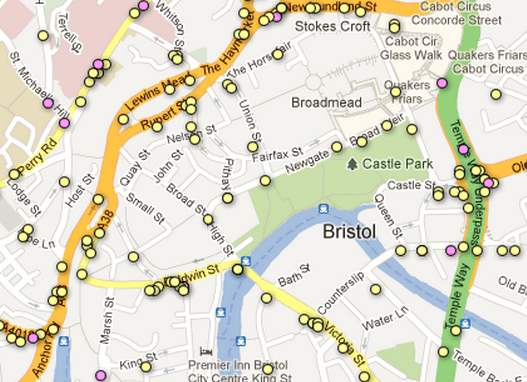
Любые указатели были бы великолепны!

Источник

2 ответа

Решение

Что ж, описание вашей проблемы читается точно так же, как алгоритм кластеризации DBSCAN (Википедия). Он избегает цепных эффектов в том смысле, что требует, чтобы они были как минимум minPts-объектами.

Что касается различий в плотности, то это то, что ОПТИКА (Википедия) должна решить. Возможно, вам придется использовать другой способ извлечения кластеров, хотя.

Ну, хорошо, может быть, не на 100% - возможно, вы хотите иметь отдельные точки доступа, а не области, которые "связаны по плотности". Размышляя о сюжете ОПТИКИ, я полагаю, что вас интересуют только маленькие, но глубокие долины, а не большие долины. Вы могли бы, вероятно, использовать OPTICS для сканирования локальных минимумов "не менее 10 аварий".

Обновление: спасибо за указатель на набор данных. Это действительно интересно. Так что я не отфильтровал это для велосипедистов, но сейчас я использую все 1,2 миллиона записей с координатами. Я добавил их в ELKI для анализа, потому что он действительно быстрый, и на самом деле он может использовать геодезическое расстояние (т.е. по широте и долготе) вместо евклидова, чтобы избежать смещения. Я включил индекс дерева R * с массовой загрузкой STR, потому что это должно значительно снизить время выполнения. Я использую OPTICS с Xi =.1, epsilon = 1 (км) и minPts = 100 (ищу только большие кластеры). Время выполнения было около 11 минут, не так уж плохо. Сюжет OPTICS, конечно, будет иметь ширину 1,2 миллиона пикселей, поэтому он больше не подходит для полной визуализации. Учитывая огромный порог, было выявлено 18 кластеров по 100-200 экземпляров в каждом. Я постараюсь визуализировать эти кластеры дальше. Но определенно попробуйте более низкие minPts для ваших экспериментов.

Итак, вот основные найденные кластеры:

  • 51.690713 -0.045545 пересечение на A10 к северу от Лондона сразу после M25
  • 51.477804 -0.404462 "Карусель вагонов"
  • 51.690713 -0.045545 "Карусель Halton Cross" или перекресток к югу от него
  • 51.436707 -0.499702 Вилка A30 и A308 Стайн-байпас
  • 53.556186 -2.489059 M61 выход к A58, к северо-западу от Манчестера
  • 55.170139 -1.532917 A189, Северная Ситон Карусель
  • 55.067229 -1.577334 A189 и A19, к югу от этого, кольцевая развязка с четырьмя переулками.
  • 51.570594 -0.096159 Manour House, Пикадилли Лайн
  • 53,477601 -1,152863 М18 и А1 (М)
  • 53.091369 -0.789684 A1, A17 и A46, сложная конструкция с перекрестками с обеих сторон A1.
  • 52,949281 -0,97896 A52 и A46
  • 50.659544 -1.15251 Остров Уайт, Сандаун.
  • ...

Обратите внимание, что это просто случайные точки, взятые из кластеров. Может быть разумно вместо этого вычислить, например, центр и радиус кластера, но я этого не делал. Я просто хотел взглянуть на этот набор данных, и это выглядит интересно.

Вот несколько скриншотов: minPts=50, epsilon=0.1, xi=0.02:

Некоторые кластеры в центре Лондона

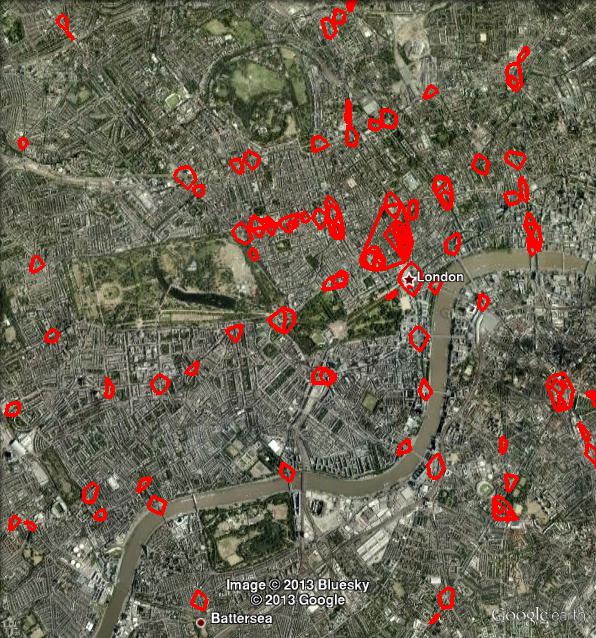
Обратите внимание, что в OPTICS кластеры могут быть иерархическими. Вот деталь:

Вложенные кластеры - ОПТИКА создает иерархию

Источник

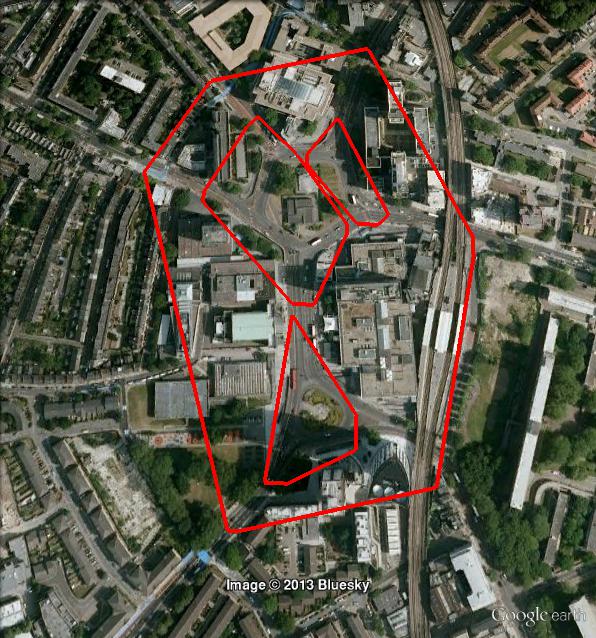
Во-первых, ваш пример вводит в заблуждение. У вас есть два разных набора данных, и вы не контролируете данные. Если он появится в цепочке, то вы получите цепочку.

Эта проблема не совсем подходит для базы данных. Вам придется написать код или найти пакет, который реализует этот алгоритм на вашей платформе.

Существует много разных алгоритмов кластеризации. Один, k-means, является итеративным алгоритмом, в котором вы ищете фиксированное количество кластеров. Для k-средних требуется несколько полных проверок данных, и, вуаля, у вас есть кластеры. Индексы не особенно полезны.

Другой подход, который обычно подходит для немного меньших наборов данных, - это иерархическая кластеризация - вы объединяете две самые близкие вещи, а затем строите кластеры. Индекс может быть полезным здесь.

Однако я рекомендую вам просмотреть сайт, такой как kdnuggets, чтобы увидеть, какое программное обеспечение - бесплатное и иное - доступно.

Источник
Другие вопросы по тегам