Поиск пути с максимальной минимальной пропускной способностью на графике

Question

Я помогаю другу в проекте, связанном с работой, где ему нужно рассчитать максимальную пропускную способность от узла a до узла b, где пропускная способность у края. Однако максимальная пропускная способность на пути от a до b ограничена ребром с наименьшей пропускной способностью.

Позвольте мне попытаться объяснить с помощью простого примера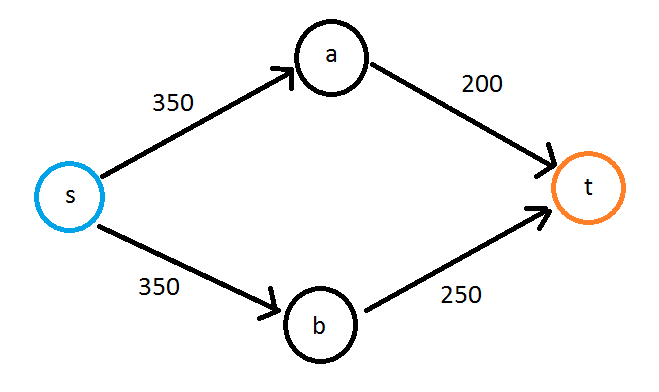

Таким образом, граф является ориентированным графом со взвешенными ребрами, и он может быть циклическим. Путь с наибольшей пропускной способностью будет s->b->t и будет иметь пропускную способность 250, поскольку этот край устанавливает предел.

Я немного прочитал и обнаружил, что этот тип проблемы является " проблемой с самым широким путем" или я бы назвал это чем-то вроде пути с максимальной минимальной емкостью, но я не нашел ни примеров, ни псевдокода, объясняющего, как заняться этим.

Я думал о том, чтобы найти все пути от s до t, использовать BFS и каким-то образом только разрешить посещение узла один раз в пути, а затем найти минимальное значение в пути, будет ли это работать?

Answer 1

Я бы использовал какой-нибудь вариант Дейкстры. Я взял псевдокод ниже прямо из Википедии и изменил только 5 маленьких вещей:

1. переименованный dist в width (из строки 3 и далее)
2. Инициализировал каждый width в -infinity (строка 3)
3. Инициализировал ширину источника infinity (строка 8)
4. Установите критерий финиша на -infinity (строка 14)
5. Модифицированы функция обновления и знак (строка 20 + 21)

1  function Dijkstra(Graph, source):
2      for each vertex v in Graph:                                 // Initializations
3          width[v] := -infinity  ;                                // Unknown width function from 
4                                                                  // source to v
5          previous[v] := undefined ;                              // Previous node in optimal path
6      end for                                                     // from source
7      
8      width[source] := infinity ;                                 // Width from source to source
9      Q := the set of all nodes in Graph ;                        // All nodes in the graph are
10                                                                 // unoptimized – thus are in Q
11      while Q is not empty:                                      // The main loop
12          u := vertex in Q with largest width in width[] ;       // Source node in first case
13          remove u from Q ;
14          if width[u] = -infinity:
15              break ;                                            // all remaining vertices are
16          end if                                                 // inaccessible from source
17          
18          for each neighbor v of u:                              // where v has not yet been 
19                                                                 // removed from Q.
20              alt := max(width[v], min(width[u], width_between(u, v))) ;
21              if alt > width[v]:                                 // Relax (u,v,a)
22                  width[v] := alt ;
23                  previous[v] := u ;
24                  decrease-key v in Q;                           // Reorder v in the Queue
25              end if
26          end for
27      end while
28      return width;
29  endfunction

Некоторое (ручное) объяснение, почему это работает: вы начинаете с источника. Оттуда у вас есть бесконечная способность к себе. Теперь вы проверяете всех соседей по источнику. Предположим, что края не все имеют одинаковую емкость (в вашем примере, скажем, (s, a) = 300). Тогда нет лучшего способа достичь b затем через (s, b), так что вы знаете лучший объем b, Вы продолжаете идти к лучшим соседям из известного набора вершин, пока не достигнете всех вершин.

Answer 2

Приведенный выше ответ был очень хорошо объяснен. На всякий случай, если кому-то понадобится объяснение правильности алгоритма, вот вам:

Доказательство:

В любой точке алгоритма будет 2 набора вершин A и B. Вершины в A будут вершинами, к которым был найден правильный путь максимальной минимальной емкости. И множество B имеет вершины, на которые мы не нашли ответа.

Индуктивная гипотеза: На любом этапе все вершины в множестве A имеют правильные значения пути максимального минимального объема к ним. т.е. все предыдущие итерации верны.

Корректность базового случая: когда множество A имеет только вершину S. Тогда значение S равно бесконечности, что является правильным.

В текущей итерации мы устанавливаем

val[W] = max(val[W], min(val[V], width_between(VW)))

Шаг индукции. Предположим, W - вершина множества B с наибольшим значением val[W]. И W исключается из очереди, и W был установлен ответ val[W].

Теперь нам нужно показать, что каждый второй путь SW имеет ширину <= val[W]. Это будет всегда верно, потому что все другие способы достижения W пройдут через какую-то другую вершину (назовите это X) в множестве B.

А для всех остальных вершин X в множестве B val[X] <= val[W]

Таким образом, любой другой путь к W будет ограничен val[X], который никогда не будет больше val[W].

Таким образом, текущая оценка val [W] является оптимальной, и, следовательно, алгоритм вычисляет правильные значения для всех вершин.