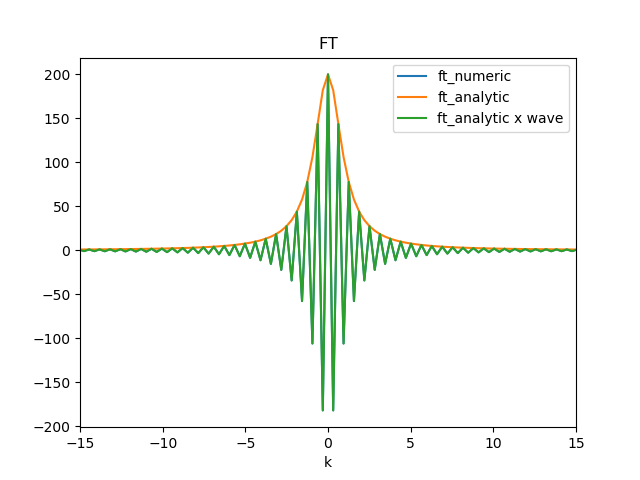
Сравнение аналитических и числовых преобразований Фурье для exp(-mod(x))

Question

Я хотел бы понять разницу между аналитическим и числовым FT функции, используя numpy.fft модуль (т.е. почему они не совпадают). Начиная с уравнения

,

можно показать, что преобразование Фурье дает аналитический FT (см., например, Arfken, Weber and Harris p966, или sympy: fourier_transform(exp(-abs(x)), x, k) который является фактором 2 * pi разные):

,

Использование python/numpy для вычисления БПФ sig = np.exp(-np.abs(x)) дает числовой FT, который может быть нанесен на график против аналитического решения (ft_numeric ~= ft_analytic x wave на графике).

Аналитический FT можно рассматривать как функцию ограничивающего окна для числового FT, и его можно превратить в числовой FT путем умножения на подходящий cos функция (ft_analytic x wave перекрывает ft_numeric, см. пример кода для формы функции).

Мой вопрос, почему это numpy БПФ производят модифицированную (модулированную космической волной) числовую ФП в этом случае? Связано ли это с тем, как определяется БПФ, и как я могу сказать это по его описанию: бесшумная реализация БПФ.

import numpy as np
import numpy.fft as fft
import pylab as plt

x = np.linspace(-10, 10, 2001)
dx = x[1] - x[0]
normalization = 1 / dx

k = 2 * np.pi * fft.fftshift(fft.fftfreq(x.shape[0], d=dx))

# Signal.
sig = np.exp(-np.abs(x))

# Both shifted.
ft_numeric = fft.fftshift(fft.fft(sig))
ft_analytic = 2 / (1 + k**2)

wave = np.cos(2 * np.pi * k / (k[2] - k[0]))

plt.figure(1)
plt.clf()
plt.title('signal')
plt.plot(x, sig)
plt.xlabel('x')

plt.figure(2)
plt.clf()
plt.title('FT')
plt.plot(k, ft_analytic.real, label='ft_analytic')
plt.plot(k, normalization * ft_numeric, label='ft_numeric')
plt.plot(k, normalization * ft_numeric * wave, label='ft_analytic x wave')
plt.xlim((-15, 15))
plt.xlabel('k')
plt.legend()

plt.show()

Answer 1

Кажется, есть фундаментальное недоразумение. Там нет кос модуляции. Вы просто отображаете действительную часть сигнала вашего числового БПФ и величину аналитики.
Реальная часть, очевидно, отражается около 0, когда вы имеете дело с реальным сигналом. Таким образом, косинус.