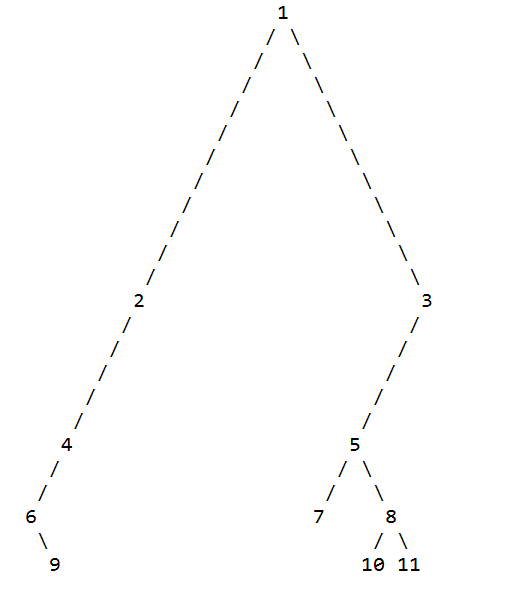Как распечатать диаграмму двоичного дерева?
Как я могу напечатать бинарное дерево на Java, чтобы вывод был похож на:
4
/ \
2 5
Мой узел:
public class Node<A extends Comparable> {
Node<A> left, right;
A data;
public Node(A data){
this.data = data;
}
}
36 ответов
Я создал простой принтер двоичного дерева. Вы можете использовать и изменять его, как хотите, но он все равно не оптимизирован. Я думаю, что здесь многое можно улучшить;)
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class BTreePrinterTest {
private static Node<Integer> test1() {
Node<Integer> root = new Node<Integer>(2);
Node<Integer> n11 = new Node<Integer>(7);
Node<Integer> n12 = new Node<Integer>(5);
Node<Integer> n21 = new Node<Integer>(2);
Node<Integer> n22 = new Node<Integer>(6);
Node<Integer> n23 = new Node<Integer>(3);
Node<Integer> n24 = new Node<Integer>(6);
Node<Integer> n31 = new Node<Integer>(5);
Node<Integer> n32 = new Node<Integer>(8);
Node<Integer> n33 = new Node<Integer>(4);
Node<Integer> n34 = new Node<Integer>(5);
Node<Integer> n35 = new Node<Integer>(8);
Node<Integer> n36 = new Node<Integer>(4);
Node<Integer> n37 = new Node<Integer>(5);
Node<Integer> n38 = new Node<Integer>(8);
root.left = n11;
root.right = n12;
n11.left = n21;
n11.right = n22;
n12.left = n23;
n12.right = n24;
n21.left = n31;
n21.right = n32;
n22.left = n33;
n22.right = n34;
n23.left = n35;
n23.right = n36;
n24.left = n37;
n24.right = n38;
return root;
}
private static Node<Integer> test2() {
Node<Integer> root = new Node<Integer>(2);
Node<Integer> n11 = new Node<Integer>(7);
Node<Integer> n12 = new Node<Integer>(5);
Node<Integer> n21 = new Node<Integer>(2);
Node<Integer> n22 = new Node<Integer>(6);
Node<Integer> n23 = new Node<Integer>(9);
Node<Integer> n31 = new Node<Integer>(5);
Node<Integer> n32 = new Node<Integer>(8);
Node<Integer> n33 = new Node<Integer>(4);
root.left = n11;
root.right = n12;
n11.left = n21;
n11.right = n22;
n12.right = n23;
n22.left = n31;
n22.right = n32;
n23.left = n33;
return root;
}
public static void main(String[] args) {
BTreePrinter.printNode(test1());
BTreePrinter.printNode(test2());
}
}
class Node<T extends Comparable<?>> {
Node<T> left, right;
T data;
public Node(T data) {
this.data = data;
}
}
class BTreePrinter {
public static <T extends Comparable<?>> void printNode(Node<T> root) {
int maxLevel = BTreePrinter.maxLevel(root);
printNodeInternal(Collections.singletonList(root), 1, maxLevel);
}
private static <T extends Comparable<?>> void printNodeInternal(List<Node<T>> nodes, int level, int maxLevel) {
if (nodes.isEmpty() || BTreePrinter.isAllElementsNull(nodes))
return;
int floor = maxLevel - level;
int endgeLines = (int) Math.pow(2, (Math.max(floor - 1, 0)));
int firstSpaces = (int) Math.pow(2, (floor)) - 1;
int betweenSpaces = (int) Math.pow(2, (floor + 1)) - 1;
BTreePrinter.printWhitespaces(firstSpaces);
List<Node<T>> newNodes = new ArrayList<Node<T>>();
for (Node<T> node : nodes) {
if (node != null) {
System.out.print(node.data);
newNodes.add(node.left);
newNodes.add(node.right);
} else {
newNodes.add(null);
newNodes.add(null);
System.out.print(" ");
}
BTreePrinter.printWhitespaces(betweenSpaces);
}
System.out.println("");
for (int i = 1; i <= endgeLines; i++) {
for (int j = 0; j < nodes.size(); j++) {
BTreePrinter.printWhitespaces(firstSpaces - i);
if (nodes.get(j) == null) {
BTreePrinter.printWhitespaces(endgeLines + endgeLines + i + 1);
continue;
}
if (nodes.get(j).left != null)
System.out.print("/");
else
BTreePrinter.printWhitespaces(1);
BTreePrinter.printWhitespaces(i + i - 1);
if (nodes.get(j).right != null)
System.out.print("\\");
else
BTreePrinter.printWhitespaces(1);
BTreePrinter.printWhitespaces(endgeLines + endgeLines - i);
}
System.out.println("");
}
printNodeInternal(newNodes, level + 1, maxLevel);
}
private static void printWhitespaces(int count) {
for (int i = 0; i < count; i++)
System.out.print(" ");
}
private static <T extends Comparable<?>> int maxLevel(Node<T> node) {
if (node == null)
return 0;
return Math.max(BTreePrinter.maxLevel(node.left), BTreePrinter.maxLevel(node.right)) + 1;
}
private static <T> boolean isAllElementsNull(List<T> list) {
for (Object object : list) {
if (object != null)
return false;
}
return true;
}
}
Выход 1:
2
/ \
/ \
/ \
/ \
7 5
/ \ / \
/ \ / \
2 6 3 6
/ \ / \ / \ / \
5 8 4 5 8 4 5 8
Выход 2:
2
/ \
/ \
/ \
/ \
7 5
/ \ \
/ \ \
2 6 9
/ \ /
5 8 4
Распечатать [большое] дерево по линиям.
пример вывода:
└── z
├── c
│ ├── a
│ └── b
├── d
├── e
│ └── asdf
└── f
код:
public class TreeNode {
final String name;
final List<TreeNode> children;
public TreeNode(String name, List<TreeNode> children) {
this.name = name;
this.children = children;
}
public void print() {
print("", true);
}
private void print(String prefix, boolean isTail) {
System.out.println(prefix + (isTail ? "└── " : "├── ") + name);
for (int i = 0; i < children.size() - 1; i++) {
children.get(i).print(prefix + (isTail ? " " : "│ "), false);
}
if (children.size() > 0) {
children.get(children.size() - 1)
.print(prefix + (isTail ?" " : "│ "), true);
}
}
}
PS Извините, этот ответ точно не фокусируется на "двоичных" деревьях. Он просто гуглится, когда запрашивает что-то для печати дерева. Решение вдохновлено командой "tree" в linux.
Я сделал улучшенный алгоритм для этого, который прекрасно обрабатывает узлы с разным размером. Он печатает сверху вниз, используя линии.
package alg;
import java.util.ArrayList;
import java.util.List;
/**
* Binary tree printer
*
* @author MightyPork
*/
public class TreePrinter
{
/** Node that can be printed */
public interface PrintableNode
{
/** Get left child */
PrintableNode getLeft();
/** Get right child */
PrintableNode getRight();
/** Get text to be printed */
String getText();
}
/**
* Print a tree
*
* @param root
* tree root node
*/
public static void print(PrintableNode root)
{
List<List<String>> lines = new ArrayList<List<String>>();
List<PrintableNode> level = new ArrayList<PrintableNode>();
List<PrintableNode> next = new ArrayList<PrintableNode>();
level.add(root);
int nn = 1;
int widest = 0;
while (nn != 0) {
List<String> line = new ArrayList<String>();
nn = 0;
for (PrintableNode n : level) {
if (n == null) {
line.add(null);
next.add(null);
next.add(null);
} else {
String aa = n.getText();
line.add(aa);
if (aa.length() > widest) widest = aa.length();
next.add(n.getLeft());
next.add(n.getRight());
if (n.getLeft() != null) nn++;
if (n.getRight() != null) nn++;
}
}
if (widest % 2 == 1) widest++;
lines.add(line);
List<PrintableNode> tmp = level;
level = next;
next = tmp;
next.clear();
}
int perpiece = lines.get(lines.size() - 1).size() * (widest + 4);
for (int i = 0; i < lines.size(); i++) {
List<String> line = lines.get(i);
int hpw = (int) Math.floor(perpiece / 2f) - 1;
if (i > 0) {
for (int j = 0; j < line.size(); j++) {
// split node
char c = ' ';
if (j % 2 == 1) {
if (line.get(j - 1) != null) {
c = (line.get(j) != null) ? '┴' : '┘';
} else {
if (j < line.size() && line.get(j) != null) c = '└';
}
}
System.out.print(c);
// lines and spaces
if (line.get(j) == null) {
for (int k = 0; k < perpiece - 1; k++) {
System.out.print(" ");
}
} else {
for (int k = 0; k < hpw; k++) {
System.out.print(j % 2 == 0 ? " " : "─");
}
System.out.print(j % 2 == 0 ? "┌" : "┐");
for (int k = 0; k < hpw; k++) {
System.out.print(j % 2 == 0 ? "─" : " ");
}
}
}
System.out.println();
}
// print line of numbers
for (int j = 0; j < line.size(); j++) {
String f = line.get(j);
if (f == null) f = "";
int gap1 = (int) Math.ceil(perpiece / 2f - f.length() / 2f);
int gap2 = (int) Math.floor(perpiece / 2f - f.length() / 2f);
// a number
for (int k = 0; k < gap1; k++) {
System.out.print(" ");
}
System.out.print(f);
for (int k = 0; k < gap2; k++) {
System.out.print(" ");
}
}
System.out.println();
perpiece /= 2;
}
}
}
Чтобы использовать это для своего дерева, пусть ваш Node реализовать класс PrintableNode,
Пример вывода:
2952:0
┌───────────────────────┴───────────────────────┐
1249:-1 5866:0
┌───────────┴───────────┐ ┌───────────┴───────────┐
491:-1 1572:0 4786:1 6190:0
┌─────┘ └─────┐ ┌─────┴─────┐
339:0 5717:0 6061:0 6271:0
public static class Node<T extends Comparable<T>> {
T value;
Node<T> left, right;
public void insertToTree(T v) {
if (value == null) {
value = v;
return;
}
if (v.compareTo(value) < 0) {
if (left == null) {
left = new Node<T>();
}
left.insertToTree(v);
} else {
if (right == null) {
right = new Node<T>();
}
right.insertToTree(v);
}
}
public void printTree(OutputStreamWriter out) throws IOException {
if (right != null) {
right.printTree(out, true, "");
}
printNodeValue(out);
if (left != null) {
left.printTree(out, false, "");
}
}
private void printNodeValue(OutputStreamWriter out) throws IOException {
if (value == null) {
out.write("<null>");
} else {
out.write(value.toString());
}
out.write('\n');
}
// use string and not stringbuffer on purpose as we need to change the indent at each recursion
private void printTree(OutputStreamWriter out, boolean isRight, String indent) throws IOException {
if (right != null) {
right.printTree(out, true, indent + (isRight ? " " : " | "));
}
out.write(indent);
if (isRight) {
out.write(" /");
} else {
out.write(" \\");
}
out.write("----- ");
printNodeValue(out);
if (left != null) {
left.printTree(out, false, indent + (isRight ? " | " : " "));
}
}
}
напечатает:
/----- 20
| \----- 15
/----- 14
| \----- 13
/----- 12
| | /----- 11
| \----- 10
| \----- 9
8
| /----- 7
| /----- 6
| | \----- 5
\----- 4
| /----- 3
\----- 2
\----- 1
для ввода
8 4 12 2 6 10 14 1 3 5 7 9 11 13 20 15
это вариант ответа @anurag - мне было жаль видеть лишние |s
Адаптировано из ответа VasyaNovikov, чтобы сделать его более двоичным, и использовать StringBuilder для эффективности (объединение String объекты вместе в Java вообще неэффективны).
public StringBuilder toString(StringBuilder prefix, boolean isTail, StringBuilder sb) {
if(right!=null) {
right.toString(new StringBuilder().append(prefix).append(isTail ? "│ " : " "), false, sb);
}
sb.append(prefix).append(isTail ? "└── " : "┌── ").append(value.toString()).append("\n");
if(left!=null) {
left.toString(new StringBuilder().append(prefix).append(isTail ? " " : "│ "), true, sb);
}
return sb;
}
@Override
public String toString() {
return this.toString(new StringBuilder(), true, new StringBuilder()).toString();
}
Выход:
│ ┌── 7
│ ┌── 6
│ │ └── 5
└── 4
│ ┌── 3
└── 2
└── 1
└── 0
Я нашел ответ ВасяНовикова очень полезным для печати большого общего дерева и изменил его для бинарного дерева
Код:
class TreeNode {
Integer data = null;
TreeNode left = null;
TreeNode right = null;
TreeNode(Integer data) {this.data = data;}
public void print() {
print("", this, false);
}
public void print(String prefix, TreeNode n, boolean isLeft) {
if (n != null) {
System.out.println (prefix + (isLeft ? "|-- " : "\\-- ") + n.data);
print(prefix + (isLeft ? "| " : " "), n.left, true);
print(prefix + (isLeft ? "| " : " "), n.right, false);
}
}
}
Образец вывода:
\-- 7
|-- 3
| |-- 1
| | \-- 2
| \-- 5
| |-- 4
| \-- 6
\-- 11
|-- 9
| |-- 8
| \-- 10
\-- 13
|-- 12
\-- 14
Мичал.креузман хороший, я должен сказать. Я чувствовал себя ленивым, чтобы сделать программу самостоятельно и искать код в сети, когда я обнаружил, что это действительно помогло мне. Но я боюсь увидеть, что он работает только для однозначных цифр, как будто вы собираетесь использовать более одной цифры, так как вы используете пробелы, а не символы табуляции, структура будет потеряна, и программа потеряет свое использование. Что касается моих более поздних кодов, мне потребовалось несколько больших входных данных (по крайней мере, больше 10), это не сработало для меня, и после поисков в сети, когда я ничего не нашел, я сам создал программу. У него есть некоторые ошибки, опять же, сейчас мне лень их исправлять, но он печатает очень красиво, и узлы могут принимать любое большое значение.
Дерево не будет таким, как упоминалось в вопросе, но оно повернуто на 270 градусов:)
public static void printBinaryTree(TreeNode root, int level){
if(root==null)
return;
printBinaryTree(root.right, level+1);
if(level!=0){
for(int i=0;i<level-1;i++)
System.out.print("|\t");
System.out.println("|-------"+root.val);
}
else
System.out.println(root.val);
printBinaryTree(root.left, level+1);
}
Поместите эту функцию с вашим собственным указанным TreeNode и оставьте уровень 0.
и наслаждаться. Вот некоторые примеры выходных данных.
| | |-------11
| |-------10
| | |-------9
|-------8
| | |-------7
| |-------6
| | |-------5
4
| |-------3
|-------2
| |-------1
| | | |-------10
| | |-------9
| |-------8
| | |-------7
|-------6
| |-------5
4
| |-------3
|-------2
| |-------1
Единственная проблема - с расширяющимися ветвями. Я постараюсь решить проблему как можно скорее, но до тех пор вы тоже можете ее использовать.
Вашему дереву потребуется удвоенное расстояние для каждого слоя:
/ \
/ \
/ \
/ \
До нашей эры
/ \ / \
/ \ / \
DEFG
/ \ / \ / \ / \
h i j k l m n oВы можете сохранить свое дерево в массиве массивов, один массив для каждой глубины:
[[А], [Ь, с], [д, е, е, ж], [H, I, J, K, L, M, N, O]]
Если ваше дерево не заполнено, вам нужно включить пустые значения в этот массив:
/ \
/ \
/ \
/ \
До нашей эры
/ \ / \
/ \ / \
DEFG
/ \ \ / \ \
h i k l m o
[[a],[b,c],[d,e,f,g],[h,i, k,l,m,,o]]Затем вы можете выполнить итерацию по массиву, чтобы напечатать ваше дерево, печатая пробелы перед первым элементом и между элементами в зависимости от глубины и печатая строки в зависимости от того, заполнены ли соответствующие элементы в массиве для следующего слоя или нет. Если ваши значения могут быть длиной более одного символа, вам нужно найти самое длинное значение при создании представления массива и соответственно умножить всю ширину и количество строк.
Решение на языке Scala, аналогичное тому, что я написал в Java:
case class Node(name: String, children: Node*) {
def toTree: String = toTree("", "").mkString("\n")
private def toTree(prefix: String, childrenPrefix: String): Seq[String] = {
val firstLine = prefix + this.name
val firstChildren = this.children.dropRight(1).flatMap { child =>
child.toTree(childrenPrefix + "├── ", childrenPrefix + "│ ")
}
val lastChild = this.children.takeRight(1).flatMap { child =>
child.toTree(childrenPrefix + "└── ", childrenPrefix + " ")
}
firstLine +: firstChildren ++: lastChild
}
}
Пример вывода:
vasya
├── frosya
│ ├── petya
│ │ └── masha
│ └── kolya
└── frosya2
По сравнению с Java-решением, у него нет ненужного отступа и содержимого. Stringнемного лучше (StringBuilder под капотом). Это все еще может вызвать исключение Stackru для глубоко вложенного дерева. Возможности для совершенствования.;-)
Я знаю, что у вас всех есть отличное решение; Я просто хочу поделиться своим - возможно, это не лучший способ, но он идеально подходит для меня!
С python а также pip на самом деле это довольно просто! БУМ!
На Mac или Ubuntu (у меня есть Mac)
- открытый терминал
$ pip install drawtree$pythonвведите консоль Python; Вы можете сделать это по-другомуfrom drawtree import draw_level_orderdraw_level_order('{2,1,3,0,7,9,1,2,#,1,0,#,#,8,8,#,#,#,#,7}')
СДЕЛАННЫЙ!
2
/ \
/ \
/ \
1 3
/ \ / \
0 7 9 1
/ / \ / \
2 1 0 8 8
/
7
Отслеживание источника:
Прежде чем я увидел этот пост, я пошел Google "бинарное дерево простого текста"
И я нашел это https://www.reddit.com/r/learnpython/comments/3naiq8/draw_binary_tree_in_plain_text/, направьте меня на этот https://github.com/msbanik/drawtree
На основании ответа ВасяНовикова. Улучшено с помощью магии Java: универсальный и функциональный интерфейс.
/**
* Print a tree structure in a pretty ASCII fromat.
* @param prefix Currnet previx. Use "" in initial call!
* @param node The current node. Pass the root node of your tree in initial call.
* @param getChildrenFunc A {@link Function} that returns the children of a given node.
* @param isTail Is node the last of its sibblings. Use true in initial call. (This is needed for pretty printing.)
* @param <T> The type of your nodes. Anything that has a toString can be used.
*/
private <T> void printTreeRec(String prefix, T node, Function<T, List<T>> getChildrenFunc, boolean isTail) {
String nodeName = node.toString();
String nodeConnection = isTail ? "└── " : "├── ";
log.debug(prefix + nodeConnection + nodeName);
List<T> children = getChildrenFunc.apply(node);
for (int i = 0; i < children.size(); i++) {
String newPrefix = prefix + (isTail ? " " : "│ ");
printTreeRec(newPrefix, children.get(i), getChildrenFunc, i == children.size()-1);
}
}
Пример начального вызова:
Function<ChecksumModel, List<ChecksumModel>> getChildrenFunc = node -> getChildrenOf(node)
printTreeRec("", rootNode, getChildrenFunc, true);
Будет выводить что-то вроде
└── rootNode
├── childNode1
├── childNode2
│ ├── childNode2.1
│ ├── childNode2.2
│ └── childNode2.3
├── childNode3
└── childNode4
Для тех, кто ищет решение для Rust:
pub struct Node {
pub value: i32,
left: Option<Box<Node>>,
right: Option<Box<Node>>
}
impl Node {
pub fn new(val: i32) -> Node {
Node {
value: val,
left: None,
right: None
}
}
pub fn getLeftNode(&self) -> Option<&Node> {
self.left.as_deref()
}
pub fn getRightNode(&self) -> Option<&Node> {
self.right.as_deref()
}
pub fn setLeftNode(&mut self, val: i32) -> &mut Node {
self.left = Some(Box::new(Node::new(val)));
self.left.as_deref_mut().unwrap()
}
pub fn setRightNode(&mut self, val: i32) -> &mut Node {
self.right = Some(Box::new(Node::new(val)));
self.right.as_deref_mut().unwrap()
}
fn visualizeTree(&self, level: u16, is_tail: bool, columns: &mut HashSet<u16>) {
let left = self.getLeftNode();
let right = self.getRightNode();
if right.is_some() {
right.unwrap().visualizeTree(level+1, false, columns);
}
if level > 0 {
for i in 0..level-1 {
if columns.contains(&i) {
print!("│ ");
} else {
print!(" ");
}
}
if is_tail {
println!("└── {}", self.value);
columns.remove(&(level-1));
columns.insert(level);
} else {
println!("┌── {}", self.value);
columns.insert(level);
columns.insert(level-1);
}
} else {
println!("{}", self.value);
}
if left.is_some() {
left.unwrap().visualizeTree(level+1, true, columns);
}
}
pub fn printTree(&self) {
let mut columns = HashSet::new();
columns.insert(0);
self.visualizeTree(0, true, &mut columns);
}
}
Результат будет примерно таким:
┌── 17
│ │ ┌── 3
│ │ │ └── 9
│ └── 2
│ └── 1
20
│ ┌── 7
│ │ │ ┌── 16
│ │ └── 15
└── 8
│ ┌── 11
└── 4
└── 13
Это было самое простое решение для горизонтального обзора. Пробовал с кучей примеров. Хорошо работает для моей цели. Обновлено с ответа @nitin-k.
public void print(String prefix, BTNode n, boolean isLeft) {
if (n != null) {
print(prefix + " ", n.right, false);
System.out.println (prefix + ("|-- ") + n.data);
print(prefix + " ", n.left, true);
}
}
Вызов:
bst.print("", bst.root, false);
Решение:
|-- 80
|-- 70
|-- 60
|-- 50
|-- 40
|-- 30
|-- 20
|-- 10
Вот класс (± 60 строк), который может создать такую строку:
330
┌──────┴──────┐
101 1738
└─┐ ┌──┴──┐
198 467 1922
┌─┘ └─┐ └─┐
154 648 1924
└─┐ ┌─────┴──────┐
155 621 1524
┌─┘ ┌────┴─────┐
576 987 1531
└─┐ ┌──┴──┐ ┌─┘
617 703 1079 1527
┌─┘
1066
Код предполагаетNodeкласс сleft,rightиdataполя. Если, например, у вас естьNode root, нижеприведенноеTreeFormatterможно использовать следующим образом:
TreeFormatter formatter = new TreeFormatter();
System.out.println(formatter.topDown(root));
Сам класс:
class TreeFormatter {
int padding = 2; // minimum number of horizontal spaces between two node data
private int indent(List<String> lines, int margin) {
// If negative, prefix all lines with spaces and return 0
if (margin >= 0) return margin;
String spaces = " ".repeat(-margin);
int i = 0;
for (var line : lines) {
lines.set(i++, spaces + line);
}
return 0;
}
private List<String> merge(List<String> left, List<String> right) {
// Merge two arrays, where the right strings are indented so there is no overlap
int minSize = Math.min(left.size(), right.size());
int offset = 0;
for (int i = 0; i < minSize; i++) {
offset = Math.max(offset, left.get(i).length() + padding - right.get(i).replaceAll("\\S.*", "").length());
}
indent(right, -indent(left, offset));
for (int i = 0; i < minSize; i++) {
left.set(i, left.get(i) + right.get(i).substring(left.get(i).length()));
}
if (right.size() > minSize) {
left.addAll(right.subList(minSize, right.size()));
}
return left;
}
private List<String> buildLines(Node node) {
if (node == null) return new ArrayList<>();
List<String> lines = merge(buildLines(node.left), buildLines(node.right));
int half = String.valueOf(node.data).length() / 2;
int i = half;
if (lines.size() > 0) {
String line;
i = lines.get(0).indexOf("*"); // Find index of first subtree
if (node.right == null) {
line = " ".repeat(i) + "┌─┘";
i += 2;
} else if (node.left == null) {
line = " ".repeat(i = indent(lines, i - 2)) + "└─┐";
} else {
int dist = lines.get(0).length() - 1 - i; // Find distance between subtree roots
line = String.format("%s┌%s┴%s┐", " ".repeat(i), "─".repeat(dist / 2 - 1), "─".repeat((dist - 1) / 2));
i += dist / 2;
}
lines.set(0, line);
}
lines.add(0, " ".repeat(indent(lines, i - half)) + node.data);
lines.add(0, " ".repeat(i + Math.max(0, half - i)) + "*"); // Add a marker for caller
return lines;
}
public String topDown(Node root) {
List<String> lines = buildLines(root);
return String.join("\n", lines.subList(1, lines.size()));
}
}
private StringBuilder prettyPrint(Node root, int currentHeight, int totalHeight) {
StringBuilder sb = new StringBuilder();
int spaces = getSpaceCount(totalHeight-currentHeight + 1);
if(root == null) {
//create a 'spatial' block and return it
String row = String.format("%"+(2*spaces+1)+"s%n", "");
//now repeat this row space+1 times
String block = new String(new char[spaces+1]).replace("\0", row);
return new StringBuilder(block);
}
if(currentHeight==totalHeight) return new StringBuilder(root.data+"");
int slashes = getSlashCount(totalHeight-currentHeight +1);
sb.append(String.format("%"+(spaces+1)+"s%"+spaces+"s", root.data+"", ""));
sb.append("\n");
//now print / and \
// but make sure that left and right exists
char leftSlash = root.left == null? ' ':'/';
char rightSlash = root.right==null? ' ':'\\';
int spaceInBetween = 1;
for(int i=0, space = spaces-1; i<slashes; i++, space --, spaceInBetween+=2) {
for(int j=0; j<space; j++) sb.append(" ");
sb.append(leftSlash);
for(int j=0; j<spaceInBetween; j++) sb.append(" ");
sb.append(rightSlash+"");
for(int j=0; j<space; j++) sb.append(" ");
sb.append("\n");
}
//sb.append("\n");
//now get string representations of left and right subtrees
StringBuilder leftTree = prettyPrint(root.left, currentHeight+1, totalHeight);
StringBuilder rightTree = prettyPrint(root.right, currentHeight+1, totalHeight);
// now line by line print the trees side by side
Scanner leftScanner = new Scanner(leftTree.toString());
Scanner rightScanner = new Scanner(rightTree.toString());
// spaceInBetween+=1;
while(leftScanner.hasNextLine()) {
if(currentHeight==totalHeight-1) {
sb.append(String.format("%-2s %2s", leftScanner.nextLine(), rightScanner.nextLine()));
sb.append("\n");
spaceInBetween-=2;
}
else {
sb.append(leftScanner.nextLine());
sb.append(" ");
sb.append(rightScanner.nextLine()+"\n");
}
}
return sb;
}
private int getSpaceCount(int height) {
return (int) (3*Math.pow(2, height-2)-1);
}
private int getSlashCount(int height) {
if(height <= 3) return height -1;
return (int) (3*Math.pow(2, height-3)-1);
}
https://github.com/murtraja/java-binary-tree-printer
работает только от 1 до 2 цифр (мне было лень, чтобы сделать его универсальным)
Я написал двоичное дерево принтер на Java.
Код есть на GitHub здесь.
Он не был оптимизирован для эффективности во время выполнения, но, поскольку мы говорим о печати в ASCII, я решил, что он не будет использоваться на очень больших деревьях. У этого есть некоторые хорошие особенности все же.
- Это позволяет эффективно использовать пространство, поскольку большое поддерево максимально расширяется под меньшее.
- Там есть параметр для установки минимального горизонтального пространства между метками узла.
- Метки узла - это строки произвольной длины.
- В дополнение к способу печати отдельного дерева, есть метод для печати списка деревьев по горизонтали по всей странице (с параметром для ширины страницы), используя столько строк, сколько необходимо.
- Существует возможность печати деревьев с диагональными ветвями (используя символы косой черты и обратной косой черты) или с горизонтальными ветвями (используя символы рисования ascii box). Последний более компактен и делает уровни дерева более наглядными.
- Оно работает.
Некоторые демонстрационные / тестовые программы включены.
Ниже приведен пример случайно сгенерированного двоичного дерева, напечатанного программой. Это иллюстрирует эффективное использование пространства с большим правым поддеревом, простирающимся под маленьким левым поддеревом:
seven
/ \
/ \
/ \
/ \
/ \
/ \
five thirteen
/ \ / \
/ \ / \
/ \ / \
three six / \
/ \ / \
/ \ / \
one four / \
\ / \
two / \
nine twenty four
/ \ / \
/ \ / \
/ \ / \
eight twelve / \
/ / \
ten / \
\ / \
eleven / \
/ \
/ \
/ \
eighteen twenty seven
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ twenty five twenty eight
/ \ \ \
/ \ twenty six thirty
fourteen nineteen /
\ \ twenty nine
sixteen twenty three
/ \ /
/ \ twenty two
/ \ /
/ \ twenty
/ \ \
fifteen seventeen twenty one
Пример печати всех пяти узловых двоичных деревьев (с метками в порядке) на странице:
one one one one one one one
\ \ \ \ \ \ \
two two two two two three three
\ \ \ \ \ / \ / \
three three four five five two four two five
\ \ / \ / / \ /
four five / \ three four five four
\ / three five \ /
five four four three
one one one one one one one two
\ \ \ \ \ \ \ / \
four four five five five five five / \
/ \ / \ / / / / / one three
two five / \ two two three four four \
\ three five \ \ / \ / / four
three / three four two four two three \
two \ / \ / five
four three three two
two two two two three three three
/ \ / \ / \ / \ / \ / \ / \
/ \ one four one five one five one four / \ two four
one three / \ / / \ \ / \ / \
\ / \ three four two five one five one five
five three five \ / \ /
/ four three two four
four
three four four four four four five
/ \ / \ / \ / \ / \ / \ /
two five one five one five two five / \ / \ one
/ / \ \ / \ three five three five \
one four two three / \ / / two
\ / one three one two \
three two \ / three
two one \
four
five five five five five five five five
/ / / / / / / /
one one one one two two three three
\ \ \ \ / \ / \ / \ / \
two three four four / \ one four one four two four
\ / \ / / one three / \ /
four two four two three \ three two one
/ \ / four
three three two
five five five five five
/ / / / /
four four four four four
/ / / / /
one one two three three
\ \ / \ / /
two three / \ one two
\ / one three \ /
three two two one
Ниже приведен пример того же дерева, напечатанного 4 разными способами, с горизонтальным интервалом 1 и 3 и с диагональными и горизонтальными ветвями.
27
┌─────┴─────┐
13 29
┌──────┴──────┐ ┌─┴─┐
8 23 28 30
┌──┴──┐ ┌──┴──┐
4 11 21 26
┌─┴─┐ ┌┴┐ ┌─┴─┐ ┌┘
2 5 9 12 18 22 24
┌┴┐ └┐ └┐ ┌─┴─┐ └┐
1 3 6 10 17 19 25
└┐ ┌┘ └┐
7 15 20
┌─┴─┐
14 16
27
/ \
/ \
13 29
/ \ / \
/ \ 28 30
/ \
/ \
/ \
/ \
8 23
/ \ / \
/ \ / \
4 11 / \
/ \ / \ 21 26
2 5 9 12 / \ /
/ \ \ \ 18 22 24
1 3 6 10 / \ \
\ 17 19 25
7 / \
15 20
/ \
14 16
27
┌────────┴────────┐
13 29
┌─────────┴─────────┐ ┌──┴──┐
8 23 28 30
┌────┴────┐ ┌────┴────┐
4 11 21 26
┌──┴──┐ ┌─┴─┐ ┌──┴──┐ ┌┘
2 5 9 12 18 22 24
┌─┴─┐ └┐ └┐ ┌──┴──┐ └┐
1 3 6 10 17 19 25
└┐ ┌┘ └┐
7 15 20
┌──┴──┐
14 16
27
/ \
/ \
/ \
/ \
13 29
/ \ / \
/ \ / \
/ \ 28 30
/ \
/ \
/ \
/ \
/ \
8 23
/ \ / \
/ \ / \
/ \ / \
4 11 / \
/ \ / \ 21 26
2 5 9 12 / \ /
/ \ \ \ / \ 24
1 3 6 10 18 22 \
\ / \ 25
7 / \
17 19
/ \
15 20
/ \
/ \
14 16
public void printPreety() {
List<TreeNode> list = new ArrayList<TreeNode>();
list.add(head);
printTree(list, getHeight(head));
}
public int getHeight(TreeNode head) {
if (head == null) {
return 0;
} else {
return 1 + Math.max(getHeight(head.left), getHeight(head.right));
}
}
/**
* pass head node in list and height of the tree
*
* @param levelNodes
* @param level
*/
private void printTree(List<TreeNode> levelNodes, int level) {
List<TreeNode> nodes = new ArrayList<TreeNode>();
//indentation for first node in given level
printIndentForLevel(level);
for (TreeNode treeNode : levelNodes) {
//print node data
System.out.print(treeNode == null?" ":treeNode.data);
//spacing between nodes
printSpacingBetweenNodes(level);
//if its not a leaf node
if(level>1){
nodes.add(treeNode == null? null:treeNode.left);
nodes.add(treeNode == null? null:treeNode.right);
}
}
System.out.println();
if(level>1){
printTree(nodes, level-1);
}
}
private void printIndentForLevel(int level){
for (int i = (int) (Math.pow(2,level-1)); i >0; i--) {
System.out.print(" ");
}
}
private void printSpacingBetweenNodes(int level){
//spacing between nodes
for (int i = (int) ((Math.pow(2,level-1))*2)-1; i >0; i--) {
System.out.print(" ");
}
}
Prints Tree in following format:
4
3 7
1 5 8
2 10
9
Это интересный вопрос, и я тоже написал для него проект.
Вот некоторые примеры:
Распечатать случайный BST.
BTPrinter.printRandomBST(100, 100);
38
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
28 82
/ \ / \
/ \ / \
/ \ / \
/ \ / \
5 31 / \
/ \ / \ / \
/ \ 30 36 / \
/ \ / / \ / \
/ \ 29 33 37 / \
/ \ / \ / \
/ \ 32 35 65 95
1 14 / / \ / \
/ \ / \ 34 / \ 94 97
0 2 / \ / \ / / \
\ 12 24 / \ 93 96 98
3 / \ / \ / \ / \
\ 9 13 16 25 / \ 84 99
4 / \ / \ \ / \ / \
7 10 15 23 26 59 74 83 86
/ \ \ / \ / \ / \ / \
6 8 11 22 27 56 60 73 76 85 91
/ / \ \ / / \ / \
20 / \ 61 67 75 79 88 92
/ \ 40 58 \ / \ / \ / \
18 21 / \ / 62 66 72 78 80 87 89
/ \ 39 54 57 \ / / \ \
17 19 / \ 64 69 77 81 90
50 55 / / \
/ \ 63 68 70
/ \ \
/ \ 71
47 53
/ \ /
/ \ 52
42 49 /
/ \ / 51
41 43 48
\
46
/
45
/
44
Распечатать дерево из массива порядка уровней в стиле leetcode, '#' означает терминатор пути, где ниже нет узла.
BTPrinter.printTree("1,2,3,4,5,#,#,6,7,8,1,#,#,#,#,#,#,2,3,4,5,6,7,8,9,10,11,12,13,14,15");
1
/ \
2 3
/ \
/ \
4 5
/ \ / \
6 7 8 1
/ \
/ \
/ \
/ \
/ \
2 3
/ \ / \
/ \ / \
4 5 6 7
/ \ / \ / \ / \
8 9 10 11 12 13 14 15
Это очень простое решение для распечатки дерева. Это не так красиво, но это действительно просто:
enum { kWidth = 6 };
void PrintSpace(int n)
{
for (int i = 0; i < n; ++i)
printf(" ");
}
void PrintTree(struct Node * root, int level)
{
if (!root) return;
PrintTree(root->right, level + 1);
PrintSpace(level * kWidth);
printf("%d", root->data);
PrintTree(root->left, level + 1);
}
Образец вывода:
106
105
104
103
102
101
100
Мне нужно было распечатать двоичное дерево в одном из моих проектов, для этого я подготовил Java-класс TreePrinter, один из выходных данных:
[+]
/ \
/ \
/ \
/ \
/ \
[*] \
/ \ [-]
[speed] [2] / \
[45] [12]Вот код для класса TreePrinter вместе с классом TextNode, Для печати любого дерева вы можете просто создать эквивалентное дерево с TextNode учебный класс.
import java.util.ArrayList;
public class TreePrinter {
public TreePrinter(){
}
public static String TreeString(TextNode root){
ArrayList layers = new ArrayList();
ArrayList bottom = new ArrayList();
FillBottom(bottom, root); DrawEdges(root);
int height = GetHeight(root);
for(int i = 0; i s.length()) min = s.length();
if(!n.isEdge) s += "[";
s += n.text;
if(!n.isEdge) s += "]";
layers.set(n.depth, s);
}
StringBuilder sb = new StringBuilder();
for(int i = 0; i temp = new ArrayList();
for(int i = 0; i 0) temp.get(i-1).left = x;
temp.add(x);
}
temp.get(count-1).left = n.left;
n.left.depth = temp.get(count-1).depth+1;
n.left = temp.get(0);
DrawEdges(temp.get(count-1).left);
}
if(n.right != null){
int count = n.right.x - (n.x + n.text.length() + 2);
ArrayList temp = new ArrayList();
for(int i = 0; i 0) temp.get(i-1).right = x;
temp.add(x);
}
temp.get(count-1).right = n.right;
n.right.depth = temp.get(count-1).depth+1;
n.right = temp.get(0);
DrawEdges(temp.get(count-1).right);
}
}
private static void FillBottom(ArrayList bottom, TextNode n){
if(n == null) return;
FillBottom(bottom, n.left);
if(!bottom.isEmpty()){
int i = bottom.size()-1;
while(bottom.get(i).isEdge) i--;
TextNode last = bottom.get(i);
if(!n.isEdge) n.x = last.x + last.text.length() + 3;
}
bottom.add(n);
FillBottom(bottom, n.right);
}
private static boolean isLeaf(TextNode n){
return (n.left == null && n.right == null);
}
private static int GetHeight(TextNode n){
if(n == null) return 0;
int l = GetHeight(n.left);
int r = GetHeight(n.right);
return Math.max(l, r) + 1;
}
}
class TextNode {
public String text;
public TextNode parent, left, right;
public boolean isEdge;
public int x, depth;
public TextNode(String text){
this.text = text;
parent = null; left = null; right = null;
isEdge = false;
x = 0; depth = 0;
}
}
Наконец, вот тестовый класс для печати данного образца:
public class Test {
public static void main(String[] args){
TextNode root = new TextNode("+");
root.left = new TextNode("*"); root.left.parent = root;
root.right = new TextNode("-"); root.right.parent = root;
root.left.left = new TextNode("speed"); root.left.left.parent = root.left;
root.left.right = new TextNode("2"); root.left.right.parent = root.left;
root.right.left = new TextNode("45"); root.right.left.parent = root.right;
root.right.right = new TextNode("12"); root.right.right.parent = root.right;
System.out.println(TreePrinter.TreeString(root));
}
}
Вы можете использовать апплет для визуализации этого очень легко. Вам необходимо распечатать следующие пункты.
Распечатать узлы в виде кругов с некоторым видимым радиусом
Получить координаты для каждого узла.
Координата x может быть визуализирована как число узлов, посещенных до того, как узел посещен в его обходе по порядку.
Координата y может быть визуализирована как глубина конкретного узла.
Распечатать строки между родителями и детьми
Это можно сделать, поддерживая координаты x и y узлов и родителей каждого узла в отдельных списках.
Для каждого узла, кроме корневого, соедините каждый узел с его родителем, взяв координаты x и y как дочернего, так и родительского.
- Вам нужно будет выровнять порядок обхода вашего дерева.
- Выберите длину узла и длину пространства.
- Получить базовую ширину дерева относительно каждого уровня, который
node_length * nodes_count + space_length * spaces_count*, - Найти связь между разветвлением, интервалом, отступом и расчетной шириной основания.
Код на GitHub: YoussefRaafatNasry / bst-ascii-визуализация
07
/\
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
03 11
/\ /\
/ \ / \
/ \ / \
/ \ / \
/ \ / \
01 05 09 13
/\ /\ /\ /\
/ \ / \ / \ / \
00 02 04 06 08 10 12 14
https://github.com/AharonSambol/PrettyPrintTreeJava
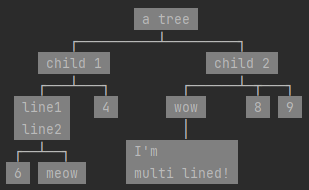
Я знаю, что опаздываю. Но я сделал это решение, которое работает не только для простых деревьев, но и для более сложных (например, многострочных строк)
Пример вывода:
Смотрите также эти ответы.
В частности, не было слишком сложно использовать abego TreeLayout для получения результатов, показанных ниже, с настройками по умолчанию.
Если вы попробуете этот инструмент, обратите внимание на следующее предостережение: он печатает детей в порядке их добавления. Для BST, где левые против правых дел, я нашел эту библиотеку неуместной без изменений.
Кроме того, метод добавления детей просто занимает parent а также child узел в качестве параметров. (Таким образом, чтобы обработать группу узлов, вы должны взять первый отдельно для создания корня.)
Я закончил тем, что использовал это решение выше, изменив его, чтобы взять в типе <Node> чтобы иметь доступ к Nodeслева и справа (дети).
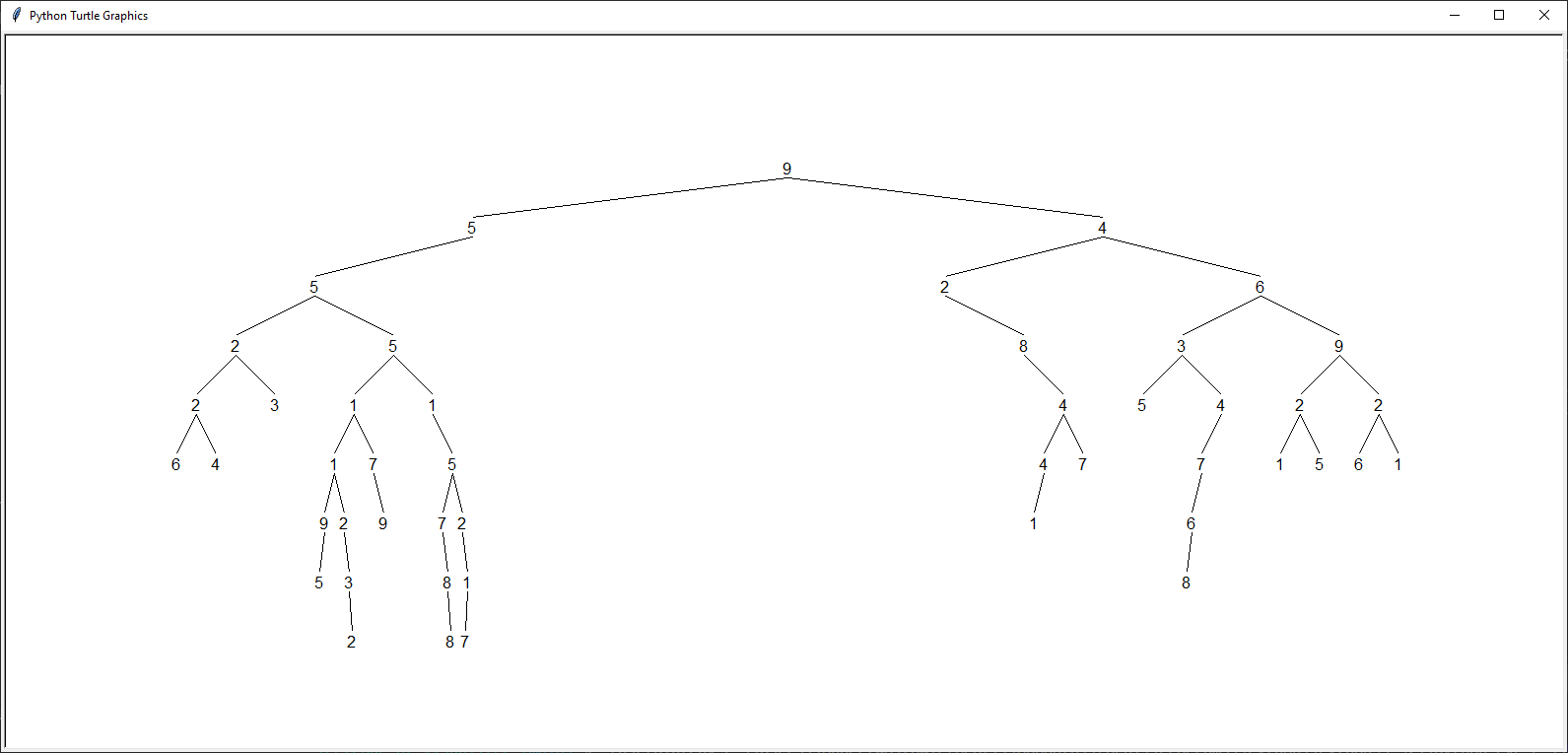
Простой код Python для визуализации двоичного дерева таблиц в стиле Leetcode размещен здесь . Также клонирован здесь
Вход:
[9,5,4,5,null,2,6,2,5,null,8,3,9,2,3,1,1,null,4,5,4,2,2,6,4,null,null,1,7,null,5,4,7,null,null,7,null,1,5,6,1,null,null,null,null,9,2,null,9,7,2,1,null,null,null,6,null,null,null,null,null,null,null,null,null,5,null,null,3,null,null,null,8,null,1,null,null,8,null,null,null,null,2,null,8,7]
Выход:
Вот очень универсальный древовидный принтер. Не самый красивый, но он справляется со многими случаями. Не стесняйтесь добавлять косые черты, если вы можете понять это. 
package com.tomac120.NodePrinter;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/**
* Created by elijah on 6/28/16.
*/
public class NodePrinter{
final private List<List<PrintableNodePosition>> nodesByRow;
int maxColumnsLeft = 0;
int maxColumnsRight = 0;
int maxTitleLength = 0;
String sep = " ";
int depth = 0;
public NodePrinter(PrintableNode rootNode, int chars_per_node){
this.setDepth(rootNode,1);
nodesByRow = new ArrayList<>(depth);
this.addNode(rootNode._getPrintableNodeInfo(),0,0);
for (int i = 0;i<chars_per_node;i++){
//sep += " ";
}
}
private void setDepth(PrintableNode info, int depth){
if (depth > this.depth){
this.depth = depth;
}
if (info._getLeftChild() != null){
this.setDepth(info._getLeftChild(),depth+1);
}
if (info._getRightChild() != null){
this.setDepth(info._getRightChild(),depth+1);
}
}
private void addNode(PrintableNodeInfo node, int level, int position){
if (position < 0 && -position > maxColumnsLeft){
maxColumnsLeft = -position;
}
if (position > 0 && position > maxColumnsRight){
maxColumnsRight = position;
}
if (node.getTitleLength() > maxTitleLength){
maxTitleLength = node.getTitleLength();
}
List<PrintableNodePosition> row = this.getRow(level);
row.add(new PrintableNodePosition(node, level, position));
level++;
int depthToUse = Math.min(depth,6);
int levelToUse = Math.min(level,6);
int offset = depthToUse - levelToUse-1;
offset = (int)(Math.pow(offset,Math.log(depthToUse)*1.4));
offset = Math.max(offset,3);
PrintableNodeInfo leftChild = node.getLeftChildInfo();
PrintableNodeInfo rightChild = node.getRightChildInfo();
if (leftChild != null){
this.addNode(leftChild,level,position-offset);
}
if (rightChild != null){
this.addNode(rightChild,level,position+offset);
}
}
private List<PrintableNodePosition> getRow(int row){
if (row > nodesByRow.size() - 1){
nodesByRow.add(new LinkedList<>());
}
return nodesByRow.get(row);
}
public void print(){
int max_chars = this.maxColumnsLeft+maxColumnsRight+1;
int level = 0;
String node_format = "%-"+this.maxTitleLength+"s";
for (List<PrintableNodePosition> pos_arr : this.nodesByRow){
String[] chars = this.getCharactersArray(pos_arr,max_chars);
String line = "";
int empty_chars = 0;
for (int i=0;i<chars.length+1;i++){
String value_i = i < chars.length ? chars[i]:null;
if (chars.length + 1 == i || value_i != null){
if (empty_chars > 0) {
System.out.print(String.format("%-" + empty_chars + "s", " "));
}
if (value_i != null){
System.out.print(String.format(node_format,value_i));
empty_chars = -1;
} else{
empty_chars = 0;
}
} else {
empty_chars++;
}
}
System.out.print("\n");
int depthToUse = Math.min(6,depth);
int line_offset = depthToUse - level;
line_offset *= 0.5;
line_offset = Math.max(0,line_offset);
for (int i=0;i<line_offset;i++){
System.out.println("");
}
level++;
}
}
private String[] getCharactersArray(List<PrintableNodePosition> nodes, int max_chars){
String[] positions = new String[max_chars+1];
for (PrintableNodePosition a : nodes){
int pos_i = maxColumnsLeft + a.column;
String title_i = a.nodeInfo.getTitleFormatted(this.maxTitleLength);
positions[pos_i] = title_i;
}
return positions;
}
}
Класс NodeInfo
package com.tomac120.NodePrinter;
/**
* Created by elijah on 6/28/16.
*/
public class PrintableNodeInfo {
public enum CLI_PRINT_COLOR {
RESET("\u001B[0m"),
BLACK("\u001B[30m"),
RED("\u001B[31m"),
GREEN("\u001B[32m"),
YELLOW("\u001B[33m"),
BLUE("\u001B[34m"),
PURPLE("\u001B[35m"),
CYAN("\u001B[36m"),
WHITE("\u001B[37m");
final String value;
CLI_PRINT_COLOR(String value){
this.value = value;
}
@Override
public String toString() {
return value;
}
}
private final String title;
private final PrintableNode leftChild;
private final PrintableNode rightChild;
private final CLI_PRINT_COLOR textColor;
public PrintableNodeInfo(String title, PrintableNode leftChild, PrintableNode rightChild){
this(title,leftChild,rightChild,CLI_PRINT_COLOR.BLACK);
}
public PrintableNodeInfo(String title, PrintableNode leftChild, PrintableNode righthild, CLI_PRINT_COLOR textColor){
this.title = title;
this.leftChild = leftChild;
this.rightChild = righthild;
this.textColor = textColor;
}
public String getTitle(){
return title;
}
public CLI_PRINT_COLOR getTextColor(){
return textColor;
}
public String getTitleFormatted(int max_chars){
return this.textColor+title+CLI_PRINT_COLOR.RESET;
/*
String title = this.title.length() > max_chars ? this.title.substring(0,max_chars+1):this.title;
boolean left = true;
while(title.length() < max_chars){
if (left){
title = " "+title;
} else {
title = title + " ";
}
}
return this.textColor+title+CLI_PRINT_COLOR.RESET;*/
}
public int getTitleLength(){
return title.length();
}
public PrintableNodeInfo getLeftChildInfo(){
if (leftChild == null){
return null;
}
return leftChild._getPrintableNodeInfo();
}
public PrintableNodeInfo getRightChildInfo(){
if (rightChild == null){
return null;
}
return rightChild._getPrintableNodeInfo();
}
}
Класс NodePosition
package com.tomac120.NodePrinter;
/**
* Created by elijah on 6/28/16.
*/
public class PrintableNodePosition implements Comparable<PrintableNodePosition> {
public final int row;
public final int column;
public final PrintableNodeInfo nodeInfo;
public PrintableNodePosition(PrintableNodeInfo nodeInfo, int row, int column){
this.row = row;
this.column = column;
this.nodeInfo = nodeInfo;
}
@Override
public int compareTo(PrintableNodePosition o) {
return Integer.compare(this.column,o.column);
}
}
И, наконец, Node Interface
package com.tomac120.NodePrinter;
/**
* Created by elijah on 6/28/16.
*/
public interface PrintableNode {
PrintableNodeInfo _getPrintableNodeInfo();
PrintableNode _getLeftChild();
PrintableNode _getRightChild();
}
Реализация ответа @MightyPork на Python:
from abc import ABC
import math
class TreePrinter:
class PrintableNode(ABC):
def getLeft(self):
pass
def getRight(self):
pass
def getText(self):
pass
def getTreeDisplay(self,root:PrintableNode):
sb=[]
lines=[]
level=[]
next=[]
level.append(root)
nn=1
widest=0
while nn!=0:
nn=0
line=[]
for n in level:
if n==None:
line.append(None)
next.append(None)
next.append(None)
else:
aa=n.getText()
line.append(aa)
if len(aa)>widest: widest=len(aa)
next.append(n.getLeft())
next.append(n.getRight())
if n.getLeft()!=None:nn+=1
if n.getRight()!=None:nn+=1
if widest%2==1:widest+=1
lines.append(line)
level=next.copy()
next=[]
perpiece=len(lines[-1])*(widest+4)
for i in range(len(lines)):
line=lines[i]
hpw=math.floor(perpiece/2.0)-1
if i>0:
for j in range(len(line)):
c=' '
if j%2==1:
if line[j-1]!=None:
c='┴' if line[j]!=None else '┘'
elif line[j]!=None:
c='└'
sb.append(c)
if line[j]==None:
sb.append(' '*(perpiece-1))
else:
for k in range(hpw):
if j%2==0: sb.append(" ")
else: sb.append("─")
if j%2==0:
sb.append("┌")
else:
sb.append("┐")
for k in range(hpw):
if j%2==0: sb.append("─")
else: sb.append(" ")
sb.append('\n')
for j in range(len(line)):
f=line[j]
if f==None:f=""
gap1=math.ceil(perpiece/2.0-len(f)/2.0)
gap2 = math.floor(perpiece / 2.0 - len(f) / 2.0)
sb.append(" "*gap1)
sb.append(f)
sb.append(" "*gap2)
sb.append("\n")
perpiece=perpiece//2
return "".join(sb)
Вот еще один способ визуализации вашего дерева: сохраните узлы в виде XML-файла, а затем позвольте вашему браузеру показать вам иерархию:
class treeNode{
int key;
treeNode left;
treeNode right;
public treeNode(int key){
this.key = key;
left = right = null;
}
public void printNode(StringBuilder output, String dir){
output.append("<node key='" + key + "' dir='" + dir + "'>");
if(left != null)
left.printNode(output, "l");
if(right != null)
right.printNode(output, "r");
output.append("</node>");
}
}
class tree{
private treeNode treeRoot;
public tree(int key){
treeRoot = new treeNode(key);
}
public void insert(int key){
insert(treeRoot, key);
}
private treeNode insert(treeNode root, int key){
if(root == null){
treeNode child = new treeNode(key);
return child;
}
if(key < root.key)
root.left = insert(root.left, key);
else if(key > root.key)
root.right = insert(root.right, key);
return root;
}
public void saveTreeAsXml(){
StringBuilder strOutput = new StringBuilder();
strOutput.append("<?xml version=\"1.0\" encoding=\"UTF-8\"?>");
treeRoot.printNode(strOutput, "root");
try {
PrintWriter writer = new PrintWriter("C:/tree.xml", "UTF-8");
writer.write(strOutput.toString());
writer.close();
}
catch (FileNotFoundException e){
}
catch(UnsupportedEncodingException e){
}
}
}
Вот код, чтобы проверить это:
tree t = new tree(1);
t.insert(10);
t.insert(5);
t.insert(4);
t.insert(20);
t.insert(40);
t.insert(30);
t.insert(80);
t.insert(60);
t.insert(50);
t.saveTreeAsXml();
И вывод выглядит так:
Визуализации стека рекурсии (Симметричного Прослеживание) наряду с печатью текущего узла :
Печать как структура каталогов:
отступы и вертикальные линии используют стек (называемый idntstck), чтобы отслеживать разделители для печати в каждой строке на основе текущей позиции стека рекурсии.
class BST:
.....
def printDFS(self, node):
self.idntstk = [' ']
if node:
print(f'==> inorder({node.value})')
self.printDfsRecur(node, 6)
def printDfsRecur(self, node, idnt):
if node:
val = node.left.value if node.left else None
self.idntPrint(idnt, f"inorder({val})")
self.idntstk.append('|')
self.printDfsRecur(node.left, idnt)
self.idntPrint(idnt, f"current({node.value})")
val = node.right.value if node.right else None
self.idntPrint(idnt, f"inorder({val})")
self.idntstk.append(' ')
self.printDfsRecur(node.right, idnt)
if self.idntstk: self.idntstk.pop()
def idntPrint(self, idnt, text):
for delim in self.idntstk:
print(delim + ' '*(idnt-1), end='')
print('|->', text)
Выход:
Pre-order Traversal: [ 1, 2, 3, 4, ]
In-order Traversal: [ 1, 2, 3, 4, ]
Post-order Traversal: [ 4, 3, 2, 1, ]
Max Height of RIGHT Skewed BST found using DFS: 4
[ 1, 2, 3, 4, ]
[ 1, 2, 3, 4, ]
[ 4, 3, 2, 1, ]
==> inorder(1)
|-> inorder(None)
|-> current(1)
|-> inorder(2)
|-> inorder(None)
|-> current(2)
|-> inorder(3)
|-> inorder(None)
|-> current(3)
|-> inorder(4)
|-> inorder(None)
|-> current(4)
|-> inorder(None)
Pre-order Traversal: [ 5, 4, 3, 2, 1, ]
In-order Traversal: [ 1, 2, 3, 4, 5, ]
Post-order Traversal: [ 1, 2, 3, 4, 5, ]
Max Height of LEFT Skewed BST found using DFS: 5
[ 5, 4, 3, 2, 1, ]
[ 1, 2, 3, 4, 5, ]
[ 1, 2, 3, 4, 5, ]
==> inorder(5)
|-> inorder(4)
| |-> inorder(3)
| | |-> inorder(2)
| | | |-> inorder(1)
| | | | |-> inorder(None)
| | | | |-> current(1)
| | | | |-> inorder(None)
| | | |-> current(2)
| | | |-> inorder(None)
| | |-> current(3)
| | |-> inorder(None)
| |-> current(4)
| |-> inorder(None)
|-> current(5)
|-> inorder(None)
Pre-order Traversal: [ 8, 3, 1, 0, 2, 6, 4, 7, 12, 10, 9, 11, 14, 13, 15, ]
In-order Traversal: [ 0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ]
Post-order Traversal: [ 0, 2, 1, 4, 7, 6, 3, 9, 11, 10, 13, 15, 14, 12, 8, ]
Max Height of BALANCED BST found using DFS: 4
[ 8, 3, 1, 0, 2, 6, 4, 7, 12, 10, 9, 11, 14, 13, 15, ]
[ 0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, ]
[ 0, 2, 1, 4, 7, 6, 3, 9, 11, 10, 13, 15, 14, 12, 8, ]
==> inorder(8)
|-> inorder(3)
| |-> inorder(1)
| | |-> inorder(0)
| | | |-> inorder(None)
| | | |-> current(0)
| | | |-> inorder(None)
| | |-> current(1)
| | |-> inorder(2)
| | |-> inorder(None)
| | |-> current(2)
| | |-> inorder(None)
| |-> current(3)
| |-> inorder(6)
| |-> inorder(4)
| | |-> inorder(None)
| | |-> current(4)
| | |-> inorder(None)
| |-> current(6)
| |-> inorder(7)
| |-> inorder(None)
| |-> current(7)
| |-> inorder(None)
|-> current(8)
|-> inorder(12)
|-> inorder(10)
| |-> inorder(9)
| | |-> inorder(None)
| | |-> current(9)
| | |-> inorder(None)
| |-> current(10)
| |-> inorder(11)
| |-> inorder(None)
| |-> current(11)
| |-> inorder(None)
|-> current(12)
|-> inorder(14)
|-> inorder(13)
| |-> inorder(None)
| |-> current(13)
| |-> inorder(None)
|-> current(14)
|-> inorder(15)
|-> inorder(None)
|-> current(15)
|-> inorder(None)
Горизонтальное представление немного сложнее по сравнению с вертикальным представлением. Вертикальная печать - это просто обход RNL(Right->Node->left или mirror of inorder), так что сначала печатается правое поддерево, а затем левое поддерево.
def printFullTree(root, delim=' ', idnt=[], left=None):
if root:
idnt.append(delim)
x, y = setDelims(left)
printFullTree(root.right, x, idnt, False)
indent2(root.val, idnt)
printFullTree(root.left, y, idnt, True)
idnt.pop()
def setDelims(left):
x = ' '; y='|'
return (y,x) if (left == True) else (x,y) if (left == False) else (x,x)
def indent2(x, idnt, width=6):
for delim in idnt:
print(delim + ' '*(width-1), end='')
print('|->', x)
output:
|-> 15
|-> 14
| |-> 13
|-> 12
| | |-> 11
| |-> 10
| |-> 9
|-> 8
| |-> 7
| |-> 6
| | |-> 4
|-> 3
| |-> 2
|-> 1
|-> 0
В горизонтальном представлении отображение строится с помощью HashMap из TreeMap или
HashMap<Integer, TreeMap<Integer, Object>> xy;где HashMap содержит ось y узла / level_no как ключ и TreeMap как значение. Древовидная карта содержит все узлы на одном уровне, отсортированные по их значению оси x как ключ, начиная с крайнего левого -ve, root = 0, крайнего правого = + ve.
Использование HashMap заставляет алгоритм работать в поиске O(1) для каждого уровня и TreeMap для сортировки в O(logn), если используется самобалансирующееся дерево / Treap.
Тем не менее, при этом не забудьте сохранить заполнители для пустого дочернего элемента, такие как '' / пробелы, чтобы дерево выглядело так, как задумано.
Теперь осталось только вычислить расстояние до горизонтального узла, это можно сделать с помощью некоторого математического вычисления,
- ширина и высота известкового дерева.
- После этого при отображении узлов представляйте их на оптимальном расстоянии на основе вычисленной ширины, высоты и информации о перекосе, если таковая имеется.