Пытаясь понять кривую Леви (фрактал)

Question

Меня просят реализовать рекурсивную функцию, которая принимает неотрицательное целое число n в качестве входных данных и возвращает инструкцию черепахи, закодированную буквами L,R и F, где L означает поворот на 45 градусов влево, R означает поворот на 45 градусов вправо и F означает движение вперед.

У меня есть дополнительная информация: для каждого неотрицательного целого числа n>0 кривая Леви L(n) можно определить с точки зрения кривой Леви L(n-1); Кривая Леви L(0) это просто прямая линия.

    usage:
    >>> lev(0)
    'F'
    >>> lev(1)
    'LFRRFL'

Я очень новичок в этом, и я не уверен, как начать:

пока что получил только

    from turtle import Screen, Turtle
    def lev(n):
        # base case
        if n ==0:
           return 'F'
        # recursive case
        else:
            return lev(n-1)

Мне нужно несколько хороших указателей здесь, пожалуйста.

Answer 1

Так как система L в Levy C имеет только одно правило, создать результирующую строку просто, используя один метод замены.

def lev(n):
    if n == 0:
        return "F"
    else:
        symbols = lev(n-1)
        return symbols.replace("F", "LFRRFL")

for i in range(4):
    print lev(i)

Результат:

F
LFRRFL
LLFRRFLRRLFRRFLL
LLLFRRFLRRLFRRFLLRRLLFRRFLRRLFRRFLLL

Вы можете визуализировать эту замену, представив, что каждая прямая линия на рисунке заменяется двумя меньшими линиями, соединенными под углом в девяносто градусов. Вот так:

Answer 2

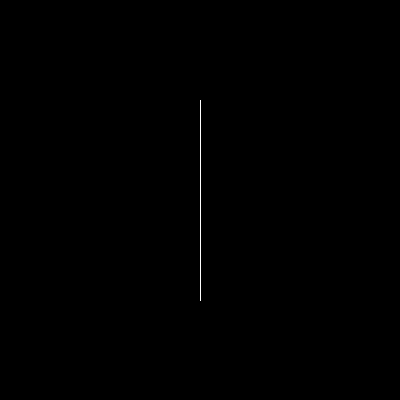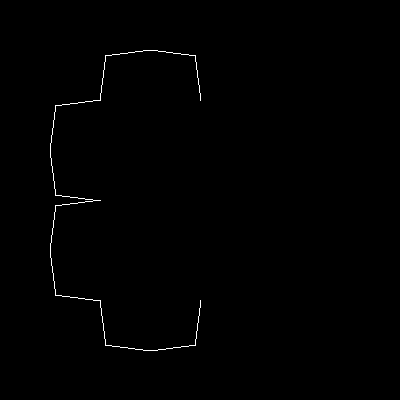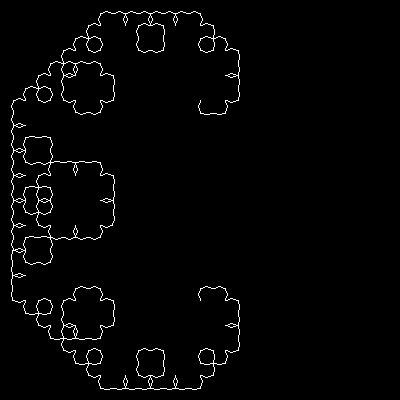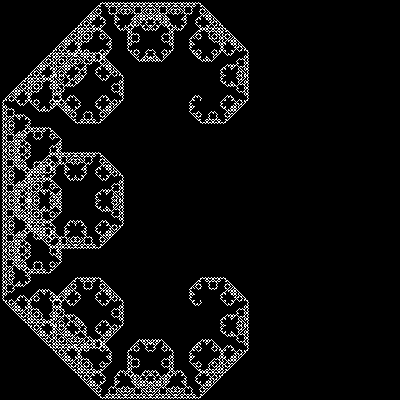
Во-первых, в случае, если это проблема: большая кривая Леви (рекурсивный случай) строится путем размещения двух меньших из них, обращенных друг к другу "поперек комнаты", с еще двумя "на полу", обращенными вверх, между ними. Маленькая кривая Леви (базовый случай) - это просто прямая линия. Итак, действительно, базовый случай:

def lev(n):
    if n == 0:
        return 'F'
    else:
        # Recursive case here

Но для рекурсивного случая вы просто вызываете lev(n-1). Вы правы, что вам нужно будет сделать это, но вам нужно будет сделать это четыре раза и вращаться между ними. Это создаст желаемые "две меньшие кривые, обращенные друг к другу, с двумя промежуточными".

Внимательно осмотрев кривую (здесь: https://en.wikipedia.org/wiki/File:Levy_C_construction.png), мы видим, что нам нужно будет нарисовать одну кривую, затем повернуть направо, затем нарисовать другую, затем полностью развернуться, затем нарисуйте третью кривую и, наконец, поверните направо и нарисуйте последнюю кривую.

Это можно сделать довольно просто:

dev lev(n):
    if n == 0:
        # Base case
        return 'F'
    else:
        # Recursive case
        # Calculate the smaller curve
        smaller = lev(n-1)
        # Add in the turning in between the smaller curves
        final = smaller        # First curve
        if n%2 == 0:           # Even depths require right turns
            final += 'RR'        # Rotate 90 degrees
            final += smaller     # Second curve
            final += 'RRRR'      # Rotate 180 degrees
            final += smaller     # Third curve
            final += 'RR'        # Rotate 90 degrees
            final += smaller     # Final curve
        else:                  # Odd depths require left turns
            final += 'LL'        # Rotate 90 degrees
            final += smaller     # Second curve
                                 # (No full rotation in odd depths)
            final += smaller     # Third curve
            final += 'LL'        # Rotate 90 degrees
            final += smaller     # Final curve
        return final           # Done!

Answer 3

Мой ответ

import turtle

def draw(n):
    l=10
    if n == 0:
        turtle.forward(l)
    else:
         turtle.left(45)
         draw(n - 1)
         turtle.right(45)
         turtle.right(45)
         draw(n-1)
         turtle.left(45)

draw(12)