Ошибка при создании объекта из шаблонного класса
Я пытался найти способ выборки случайных векторов из многомерного нормального распределения в C++, имеющего как средний вектор, так и ковариационную матрицу, во многом как в Matlab mvnrnd функция работает. Я нашел соответствующий код для класса, который реализует это на этой странице, но у меня были некоторые проблемы при компиляции. Я создал заголовочный файл, который включен в мой main.cpp, и я пытаюсь создать объект EigenMultivariateNormal учебный класс:
MatrixXd MN(10,1);
MatrixXd CVM(10,10);
EigenMultivariateNormal <double,int> (&MN,&CVM) mvn;
Проблема в том, что я получаю ошибку, связанную с шаблоном при компиляции:
error: type/value mismatch at argument 2 in template parameter list for ‘template<class _Scalar, int _size> class EigenMultivariateNormal’
error: expected a constant of type ‘int’, got ‘int’
error: expected ‘;’ before ‘mvn’
У меня есть только поверхностное представление о том, как работать с шаблонами, и я ни в коем случае не эксперт по cpp, поэтому мне было интересно, что именно я делаю неправильно? Видимо, я должен иметь const где-то в моем коде.
2 ответа
template<class _Scalar, int _size> class EigenMultivariateNormal это специализированный шаблон класса. Первый class _Scalar попросить тип, но int _size попросить инт.
Вы должны вызывать его с константой int вместо типа int, как вы это сделали. Во-вторых, ваш синтаксис для экземпляра нового класса EigenMultivariateNormal неверен. Попробуйте это вместо этого:
EigenMultivariateNormal<double, 10> mvn (&MN, &CVM); // with 10 is the size
Этот код немного стар Вот более новая, возможно улучшенная версия. Вероятно, есть еще кое-что плохое. Например, я думаю, что это должно быть изменено, чтобы использовать MatrixBase вместо фактического Matrix, Это может позволить ему оптимизировать и лучше решить, когда ему нужно выделять место для хранения или нет. Это также использует пространство имен internal что, вероятно, нахмурился, но кажется необходимым использовать Эйгена NullaryExpr что кажется правильным решением. Там использование страшных mutable ключевое слово. Это необходимо из-за того, что, по мнению Эйгена, должно быть const когда используется в NullaryExpr, Это также немного раздражает, чтобы положиться на повышение. Похоже, что в C++11 необходимые функции стали стандартными. Ниже кода класса приведен краткий пример использования.
Класс eigenmultivariatenormal.hpp
#ifndef __EIGENMULTIVARIATENORMAL_HPP
#define __EIGENMULTIVARIATENORMAL_HPP
#include <Eigen/Dense>
#include <boost/random/mersenne_twister.hpp>
#include <boost/random/normal_distribution.hpp>
/*
We need a functor that can pretend it's const,
but to be a good random number generator
it needs mutable state. The standard Eigen function
Random() just calls rand(), which changes a global
variable.
*/
namespace Eigen {
namespace internal {
template<typename Scalar>
struct scalar_normal_dist_op
{
static boost::mt19937 rng; // The uniform pseudo-random algorithm
mutable boost::normal_distribution<Scalar> norm; // The gaussian combinator
EIGEN_EMPTY_STRUCT_CTOR(scalar_normal_dist_op)
template<typename Index>
inline const Scalar operator() (Index, Index = 0) const { return norm(rng); }
};
template<typename Scalar>
boost::mt19937 scalar_normal_dist_op<Scalar>::rng;
template<typename Scalar>
struct functor_traits<scalar_normal_dist_op<Scalar> >
{ enum { Cost = 50 * NumTraits<Scalar>::MulCost, PacketAccess = false, IsRepeatable = false }; };
} // end namespace internal
/**
Find the eigen-decomposition of the covariance matrix
and then store it for sampling from a multi-variate normal
*/
template<typename Scalar, int Size>
class EigenMultivariateNormal
{
Matrix<Scalar,Size,Size> _covar;
Matrix<Scalar,Size,Size> _transform;
Matrix< Scalar, Size, 1> _mean;
internal::scalar_normal_dist_op<Scalar> randN; // Gaussian functor
public:
EigenMultivariateNormal(const Matrix<Scalar,Size,1>& mean,const Matrix<Scalar,Size,Size>& covar)
{
setMean(mean);
setCovar(covar);
}
void setMean(const Matrix<Scalar,Size,1>& mean) { _mean = mean; }
void setCovar(const Matrix<Scalar,Size,Size>& covar)
{
_covar = covar;
// Assuming that we'll be using this repeatedly,
// compute the transformation matrix that will
// be applied to unit-variance independent normals
/*
Eigen::LDLT<Eigen::Matrix<Scalar,Size,Size> > cholSolver(_covar);
// We can only use the cholesky decomposition if
// the covariance matrix is symmetric, pos-definite.
// But a covariance matrix might be pos-semi-definite.
// In that case, we'll go to an EigenSolver
if (cholSolver.info()==Eigen::Success) {
// Use cholesky solver
_transform = cholSolver.matrixL();
} else {*/
SelfAdjointEigenSolver<Matrix<Scalar,Size,Size> > eigenSolver(_covar);
_transform = eigenSolver.eigenvectors()*eigenSolver.eigenvalues().cwiseMax(0).cwiseSqrt().asDiagonal();
/*}*/
}
/// Draw nn samples from the gaussian and return them
/// as columns in a Size by nn matrix
Matrix<Scalar,Size,-1> samples(int nn)
{
return (_transform * Matrix<Scalar,Size,-1>::NullaryExpr(Size,nn,randN)).colwise() + _mean;
}
}; // end class EigenMultivariateNormal
} // end namespace Eigen
#endif
Вот простая программа, которая использует это:
#include <fstream>
#include "eigenmultivariatenormal.hpp"
#ifndef M_PI
#define M_PI REAL(3.1415926535897932384626433832795029)
#endif
/**
Take a pair of un-correlated variances.
Create a covariance matrix by correlating
them, sandwiching them in a rotation matrix.
*/
Eigen::Matrix2d genCovar(double v0,double v1,double theta)
{
Eigen::Matrix2d rot = Eigen::Rotation2Dd(theta).matrix();
return rot*Eigen::DiagonalMatrix<double,2,2>(v0,v1)*rot.transpose();
}
void main()
{
Eigen::Vector2d mean;
Eigen::Matrix2d covar;
mean << -1,0.5; // Set the mean
// Create a covariance matrix
// Much wider than it is tall
// and rotated clockwise by a bit
covar = genCovar(3,0.1,M_PI/5.0);
// Create a bivariate gaussian distribution of doubles.
// with our chosen mean and covariance
Eigen::EigenMultivariateNormal<double,2> normX(mean,covar);
std::ofstream file("samples.txt");
// Generate some samples and write them out to file
// for plotting
file << normX.samples(1000).transpose() << std::endl;
}
И вот сюжет, показывающий результаты.
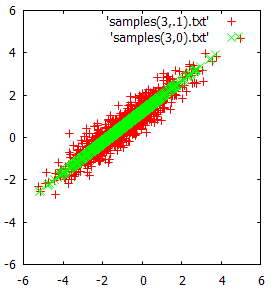
С использованием SelfAdjointEigenSolver вероятно, намного медленнее, чем разложение Холецкого, но оно устойчиво, даже если ковариационная матрица сингулярна. Если вы знаете, что ваши ковариационные матрицы всегда будут полными, вы можете использовать это вместо этого. Однако, если вы редко создаете дистрибутив и часто используете его, тогда это, вероятно, не имеет большого значения.