Степень извлечения, средняя степень из класса Graph

Question

Кто-нибудь пытался внедрить программное обеспечение для извлечения степеней, средних степеней из Graph Class of NetworkX? Я не прошу реализованные методы в networkX, который является стабильным. Я прошу здесь для реализации на чистом уровне.

Вот что я пробовал до сих пор (не уверен, что это правильно)?

for i in range(3, 9):
    G = nx.gnp_random_graph(i, 0.2) #Returns a G_{n,p} random graph, also known as an Erdős-Rényi graph or a binomial graph.
    #print(len(G))
    #print(len(G.nodes()))
    from collections import *
    import collections

    class OrderedCounter(Counter, OrderedDict):
        pass

    m=[list (i) for i in G.edges()]

    flat_list = [item for sublist in m for item in sublist]
    counterlist = OrderedCounter(flat_list)
    degree_sequence=sorted(sorted(counterlist.values(), reverse=True))
    degreeCount=collections.Counter(degree_sequence)
    print("degreeCount:", degreeCount)

    #deg, cnt = zip(*degreeCount.items()) #Returns the average degree of the neighborhood of each node.
    #print(deg, cnt)

    nodes = len(G) 
    count_Triangle = 0 #Initialize result 
    # Consider every possible triplet of edges in graph 
    for i in range(nodes): 
        for j in range(nodes): 
            for k in range(nodes): 
                # check the triplet if it satisfies the condition 
                if( i!=j and i !=k and j !=k and
                        G[i][j] and G[j][k] and G[k][i]): 
                    count_Triangle += 1
                    print(count_Triangle)

когда я считаю треугольник таким образом, я продолжаю получать Key error потому что я знаю, что индекс, который я передаю, неверен. Я думал, что G - объект dict. Не могу понять.

Также, если я пытаюсь извлечь deg, cnt выше, из которого я думал, что решение получить среднюю степень, я продолжаю получать ошибку, когда словарь пуст.

Answer 1

Для подсчета треугольников

• Диктоподобный доступ G[u][v] работает с данными ребра в графе GЗначит ключи в дикте G[u] не являются (в общем случае) всеми остальными узлами графа; хотя ключи в дикте G включите все узлы в графе.

• Если вы хотите использовать эту форму индексации, вам, вероятно, лучше создать матрицу смежности, которая содержит n x n элементов для графа n-узлов. Тогда все запросы A[i][j] для i в диапазоне [0, n] будет действительным; и возвращаемое значение будет 0, если нет ребра.

• также посмотрите на itertools, которые сделают ваш код чище..

for i,j,k in itertools.combinations(xrange(n), 3):
    # a generator of all unique combinations of [0,1,2,3,4]
    # this already excludes the cases where i==j, i==k j==k
    print(i,j,k)

хотя будьте осторожны, потому что в этом пакете есть различные функции, которые очень похожи.

Вот код, который подсчитывает количество треугольников здесь

import networkx as nx
import matplotlib.pyplot as plt
import itertools

T1 = []
T2 = []

n = 7
p = 0.2
reps = 1000
for r in xrange(reps):
    G = nx.gnp_random_graph(n, p)

    A = nx.adj_matrix(G);

    t = 0;
    for (i,j,k) in itertools.combinations(xrange(n), 3):
        # a generator of all unique 3-combinations of [0,1,2,...,n]
        if i==k or i==j or j==k:
            print ("Found a duplicate node!", i,j,k)
            continue # just skip it -- shouldn't happen
        if A[i,j] and A[j,k] and A[i,k]:
            t += 1
    T1.append(t);

    # let's check we agree with networkx built-in
    tr = nx.triangles(G)
    T2.append(sum(tr.values()))    

T2 = [t /3.0 for t in T2]; # divide all through by 3, since this is a count of the nodes of each triangle and not the number of triangles.

plt.figure(1); plt.clf()
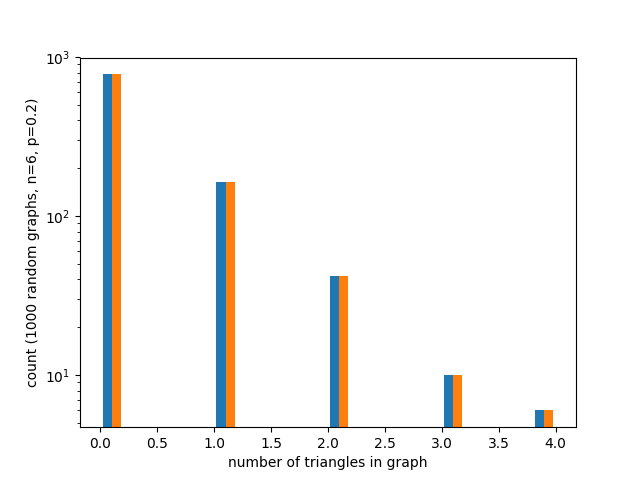
plt.hist([T1, T2], 20)

Здесь вы видите, что количество треугольников одинаково (я поместил логарифмическую шкалу по оси Y, поскольку частоты более высоких значений треугольников довольно низкие).

Для подсчета степени

Похоже, вам нужна более четкая картина того, какую степень вы хотите вычислить: - Это неориентированный граф, что означает, что если между u и v есть ребро, то оба этих узла должны быть как минимум в степени-1. Ваш расчет учитывает ребра только один раз.

Во-вторых, графики, которые вы создаете, не имеют много ребер, особенно для меньших. При p=0,2 доля 3-узловых графов без каких-либо ребер составляет 51%, и даже 5-узловые графы не будут иметь ребер 11% времени. Таким образом, пустой список не свидетельствует о сбое.

Средний уровень очень легко проверить, используя атрибуты графика:

2*G.number_of_edges() / float(G.number_of_nodes())

или встроенный калькулятор степени для каждого узла.

sum([d for (n, d) in nx.degree(G)]) / float(G.number_of_nodes())

Answer 2

В вашем коде есть две ошибки. Первый, node должен быть список узлов в графе G не длина узлов в графе. Это гарантирует, что ваша логика работает для всех графов (даже с графом, чей узел не начинается с индекса 0). Кроме того, ваши циклы for должны меняться соответственно, как это

nodes = G.nodes() #<--- Store the list of nodes 
count_Triangle = 0 #Initialize result
# Consider every possible triplet of edges in graph

for i in nodes: #<---------Iterate over the lists of nodes
    for j in nodes: 
        for k in nodes: 

Далее, вы не получаете доступ к краям графика, как индексы. Вы должны использовать метод has_edge(), потому что, если ребро отсутствует, код не потерпит неудачу.

Так что ваши if утверждение становится:

if( i!=j and i !=k and j !=k and
                    G.has_edge(i,j) and G.has_edge(j, k) and G.has_edge(k, i)):
                count_Triangle += 1
                print(count_Triangle)

Собрав все это вместе, ваша программа становится:

import networkx as nx
from collections import *
import collections

for i in range(3, 9):
    G = nx.gnp_random_graph(i, 0.2)
    class OrderedCounter(Counter, OrderedDict):
        pass

    m=[list (i) for i in G.edges()]

    flat_list = [item for sublist in m for item in sublist]
    counterlist = OrderedCounter(flat_list)
    degree_sequence=sorted(sorted(counterlist.values(), reverse=True))
    degreeCount=collections.Counter(degree_sequence)
    print("degreeCount:", degreeCount)


    #Store the list of nodes 
    nodes = G.nodes()

    count_Triangle = 0 #Initialize result
    # Consider every possible triplet of edges in graph


    for i in nodes:    #<---------Iterate over the lists of nodes
        for j in nodes:
            for k in nodes:

                # Use has_edge method
                if( i!=j and i !=k and j !=k and
                        G.has_edge(i,j) and G.has_edge(j, k) and G.has_edge(k, i)):
                    count_Triangle += 1
                    print(count_Triangle)