Какой самый быстрый способ генерации n-го числа Моцкина?
Я хочу сгенерировать все число Моцкина и сохранить в массиве. Формула дается следующим образом: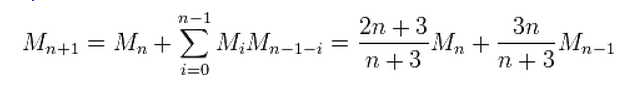
Моя текущая реализация слишком медленная:
void generate_slow() {
mm[0] = 1;
mm[1] = 1;
mm[2] = 2;
mm[3] = 4;
mm[4] = 9;
ull result;
for (int i = 5; i <= MAX_NUMBERS; ++i) {
result = mm[i - 1];
for (int k = 0; k <= (i - 2); ++k) {
result = (result + ((mm[k] * mm[i - 2 - k]) % MODULO)) % MODULO;
}
mm[i] = result;
}
}
void generate_slightly_faster() {
mm[0] = 1;
mm[1] = 1;
mm[2] = 2;
mm[3] = 4;
mm[4] = 9;
ull result;
for (int i = 5; i <= MAX_NUMBERS; ++i) {
result = mm[i - 1];
for (int l = 0, r = i - 2; l <= r; ++l, --r) {
if (l != r) {
result = (result + (2 * (mm[l] * mm[r]) % MODULO)) % MODULO;
}
else {
result = (result + ((mm[l] * mm[r]) % MODULO)) % MODULO;
}
}
mm[i] = result;
}
}
Кроме того, я застрял в поиске замкнутой формы для матрицы повторений, чтобы я мог применить возведение в степень. Кто-нибудь может предложить лучший алгоритм? Благодарю.
Изменить Я не могу применить вторую формулу, потому что деление не применяется, когда по модулю число. Максимум n равно 10000, что находится за пределами диапазона 64-разрядного целого числа, поэтому ответ по модулю с большим числом m где m = 10^14 + 7. Большая целочисленная библиотека не допускается.
2 ответа
Действительно, вы можете использовать вторую формулу. Деление может быть выполнено с помощью модульного мультипликативного обратного. Даже если модульное число не простое, что затрудняет, это также возможно (я нашел несколько полезных советов в обсуждении задачи MAXGAME):
Prime factorise MOD as = 43 * 1103 * 2083 * 1012201. Вычислите все величины по модулю каждого из этих простых чисел, а затем используйте китайскую теорему об остатках, чтобы узнать значение по модулю MOD. Остерегайтесь, так как здесь также используется деление, для каждой величины нужно поддерживать высшие силы каждого из этих простых чисел, которые также разделяют их.
Следующая программа C++ печатает первые 10000 чисел Моцкина по модулю 100000000000007:
#include <iostream>
#include <stdexcept>
// Exctended Euclidean algorithm: Takes a, b as input, and return a
// triple (g, x, y), such that ax + by = g = gcd(a, b)
// (http://en.wikibooks.org/wiki/Algorithm_Implementation/Mathematics/
// Extended_Euclidean_algorithm)
void egcd(int64_t a, int64_t b, int64_t& g, int64_t& x, int64_t& y) {
if (!a) {
g = b; x = 0; y = 1;
return;
}
int64_t gtmp, xtmp, ytmp;
egcd(b % a, a, gtmp, ytmp, xtmp);
g = gtmp; x = xtmp - (b / a) * ytmp; y = ytmp;
}
// Modular Multiplicative Inverse
bool modinv(int64_t a, int64_t mod, int64_t& ainv) {
int64_t g, x, y;
egcd(a, mod, g, x, y);
if (g != 1)
return false;
ainv = x % mod;
if (ainv < 0)
ainv += mod;
return true;
}
// returns (a * b) % mod
// uses Russian Peasant multiplication
// (http://stackru.com/a/12171020/237483)
int64_t mulmod(int64_t a, int64_t b, int64_t mod) {
if (a < 0) a += mod;
if (b < 0) b += mod;
int64_t res = 0;
while (a != 0) {
if (a & 1) res = (res + b) % mod;
a >>= 1;
b = (b << 1) % mod;
}
return res;
}
// Takes M_n-2 (m0) and M_n-1 (m1) and returns n-th Motzkin number
// all numbers are modulo mod
int64_t motzkin(int64_t m0, int64_t m1, int n, int64_t mod) {
int64_t tmp1 = ((2 * n + 3) * m1 + (3 * n * m0));
int64_t tmp2 = n + 3;
// return 0 if mod divides tmp1 because:
// 1. mod is prime
// 2. if gcd(tmp2, mod) != 1 --> no multiplicative inverse!
// --> 3. tmp2 is a multiple from mod
// 4. tmp2 divides tmp1 (Motzkin numbers aren't floating point numbers)
// --> 5. mod divides tmp1
// --> tmp1 % mod = 0
// --> (tmp1 * tmp2^(-1)) % mod = 0
if (!(tmp1 % mod))
return 0;
int64_t tmp3;
if (!modinv(tmp2, mod, tmp3))
throw std::runtime_error("No multiplicative inverse");
return (tmp1 * tmp3) % mod;
}
int main() {
const int64_t M = 100000000000007;
const int64_t MD[] = { 43, 1103, 2083, 1012201 }; // Primefactors
const int64_t MX[] = { M/MD[0], M/MD[1], M/MD[2], M/MD[3] };
int64_t e1[4];
// Precalculate e1 for the Chinese remainder algo
for (int i = 0; i < 4; i++) {
int64_t g, x, y;
egcd(MD[i], MX[i], g, x, y);
e1[i] = MX[i] * y;
if (e1[i] < 0)
e1[i] += M;
}
int64_t m0[] = { 1, 1, 1, 1 };
int64_t m1[] = { 1, 1, 1, 1 };
for (int n = 1; n < 10000; n++) {
// Motzkin number for each factor
for (int i = 0; i < 4; i++) {
int64_t tmp = motzkin(m0[i], m1[i], n, MD[i]);
m0[i] = m1[i];
m1[i] = tmp;
}
// Chinese remainder theorem
int64_t res = 0;
for (int i = 0; i < 4; i++) {
res += mulmod(m1[i], e1[i], M);
res %= M;
}
std::cout << res << std::endl;
}
return 0;
}
ПРЕДУПРЕЖДЕНИЕ: СЛЕДУЮЩИЙ КОД НЕПРАВИЛЬНЫЙ, ПОТОМУ ЧТО ИМ ИСПОЛЬЗУЕТСЯ ЦЕЛЫЙ РАЗДЕЛ (например, 5/2 = 2, а не 2.5). Не стесняйтесь исправить это!
Это хороший шанс использовать динамическое программирование. Это очень похоже на разработку чисел Фибоначчи.
sample code:
cache = {}
cache[0] = 1
cache[1] = 1
def motzkin(n):
if n in cache:
return cache[n]
else:
result = 3*n*motzkin(n - 2)/(n + 3) + (2*n + 3)*motzkin(n - 1)/(n + 3)
cache[n] = result
return result
for i in range(10):
print i, motzkin(i)
print motzkin(1000)
"""
0 1
1 1
2 2
3 4
4 9
5 21
6 53
7 134
8 346
9 906
75794754010998216916857635442484411813743978100571902845098110153309261636322340168650370511949389501344124924484495394937913240955817164730133355584393471371445661970273727286877336588424618403572614523888534965515707096904677209192772199599003176027572021460794460755760991100028703368873821893050902166740481987827822643139384161298315488092901472934255559058881743019252022468893544043541453423967661847226330177828070589283132360685783010085347614855435535263090005810
"""
Проблема в том, что эти цифры становятся такими большими, что хранение их всех в кеше закончится, если вы захотите подняться очень высоко. Тогда лучше использовать цикл for, помня предыдущие 2 условия. Если вы хотите найти число Моцкина для многих чисел, я советую сначала отсортировать ваши числа, а затем, когда вы приближаетесь к каждому из ваших чисел в цикле for, выведите результат.
РЕДАКТИРОВАТЬ: я создал зацикленную версию, но получил результаты, отличные от моей предыдущей рекурсивной функции. По крайней мере, один из них должен быть не прав!! Надеюсь, вы все еще видите, как это работает, и можете это исправить!
def motzkin2(numbers):
numbers.sort() #assumes no duplicates
up_to = 0
if numbers[0] == 0:
yield 1
up_to += 1
if 1 in numbers[:2]:
yield 1
up_to += 1
max_ = numbers[-1]
m0 = 1
m1 = 1
for n in range(3, max_ + 1):
m2 = 3*n*m0/(n + 3) + (2*n + 3)*m1/(n + 3)
if n == numbers[up_to]:
yield n, m2
up_to += 1
m0, m1 = m1, m2
for pair in motzkin2([9,1,3,7, 1000]):
print pair
"""
1
(3, 2)
(7, 57)
(9, 387)
(1000, 32369017020536373226194869003219167142048874154652342993932240158930603189131202414912032918968097703139535871364048699365879645336396657663119183721377260183677704306107525149452521761041198342393710275721776790421499235867633215952014201548763282500175566539955302783908853370899176492629575848442244003609595110883079129592139070998456707801580368040581283599846781393163004323074215163246295343379138928050636671035367010921338262011084674447731713736715411737862658025L)
"""