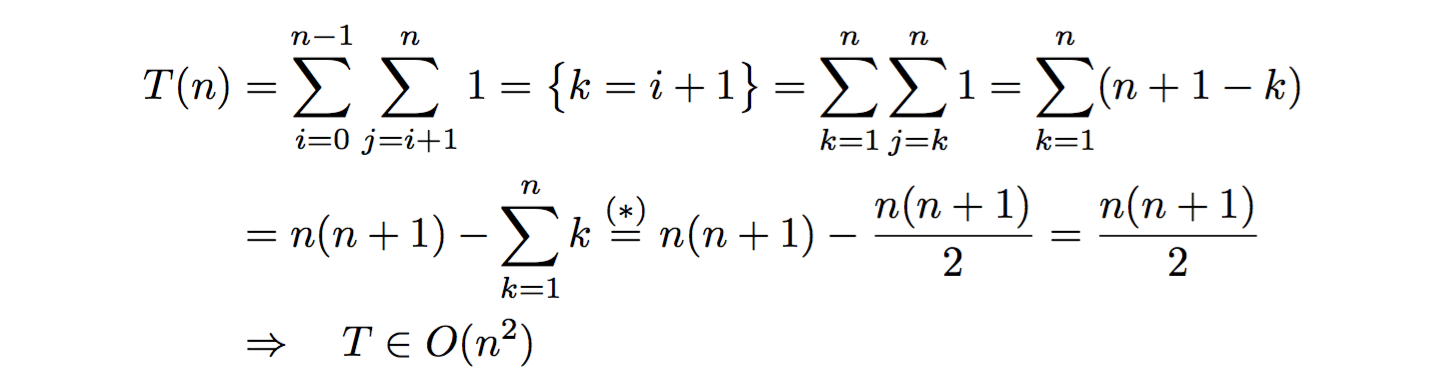Используя Big O Notation, какова правильная метка для этого алгоритма?

Question

Используя Big O Notation, какова правильная метка для этого алгоритма?

Мне интересно, как официальный способ описать это, используя Big O Notation?

var prices = [100, 180, 260, 590, 40, 310, 535, 10, 5, 3];
var biggest_profit = 0;

for (var i=0; i < prices.length; i++) {
    var first_price = prices[i];

    for (var j=i+1; j <= prices.length; j++) {
      // do something here
    }
}

Это то, что меня отталкивает:

j=i+1

Каждый раз, когда мы проходим i, j становится все короче и короче.

Какое правильное название для этого паттерна в Big O Notation?

2

algorithm time-complexity big-o

Источник

user5175938 06 авг '16 в 17:58

4 ответа

Решение

Если do something here является O(1) операция, весь алгоритм O(N^2),

Как рассчитать? (Спасибо @dfri за отлов ошибок)

Внешний цикл: i: [0->N-1]

Внутренний цикл: j: [i+1->N]

Всего = N + (N-1) + (N-2) + (N-3) + ... + 1 = N(N+1)/2 = O(N^2)

5

Источник

user4523099 06 авг '16 в 18:00

Чтобы вычислить большую O этого алгоритма, просто представьте форму: в каждой итерации внешнего цикла for у нас есть строка, состоящая из маленьких квадратов. Каждый квадрат - это одна итерация внутреннего цикла for. Так что для первой итерации внешнего цикла for у нас будет полная строка квадратов. Второй ряд, потеряет один из квадратов. А третий ряд потеряет еще один.... В последнем ряду будет только один квадрат. В итоге мы получим эту форму:

⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜_____
⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜_______
⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜________
⬜⬜⬜⬜⬜⬜⬜⬜⬜⬜_________
⬜⬜⬜⬜⬜⬜⬜⬜⬜__________
⬜⬜⬜⬜⬜⬜⬜⬜___________
⬜⬜⬜⬜⬜⬜⬜____________
⬜⬜⬜⬜⬜⬜_____________
⬜⬜⬜⬜⬜______________
⬜⬜⬜⬜_______________
⬜⬜⬜________________
⬜⬜_________________
⬜__________________

Это половина большого квадрата. Таким образом, его площадь составляет: цена. Длина * (цены. Длина - 1) * 1/2. И мы можем удалить "-1", потому что это достаточно мало. И результат: Цены. Длина * Цены. Длина * 1/2. 1/2 не важна в Big O. Таким образом, алгоритм имеет O(n^2) временную сложность.

2

Источник

user6398399 07 авг '16 в 21:09

      var prices = [100, 180, 260, 590, 40, 310, 535, 10, 5, 3];
var biggest_profit = 0;

for (var i = 0; i < prices.length; i++) {  // outer loop
    var first_price = prices[i];

    for (var j = i + 1; j <= prices.length; j++) {  // inner loop
        // do something here
    }
}

В первой итерации внешнего цикла (i = 0) внутренний цикл выполняется несколько раз.

Во второй итерации внешнего цикла (i = 1) внутренний цикл выполняется несколько раз.

В третьей итерации внешнего цикла (i = 2) внутренний цикл выполняется несколько раз.

. . .

На й итерации внешнего цикла (i = N - 3) выполняется внутренний цикл 3раз.

В й итерации внешнего цикла (i = N - 2) внутренний цикл выполняется несколько раз.

В последней (й) итерации внешнего цикла (i = N - 1) внутренний цикл выполняется time.

Таким образом, общее количество выполнений этого кода равно

+ + + + … + +

знак равно 1+ 2+ … + N - 3+ N - 2+ N - 1+ N

Подставив это в формулу суммы натуральных чисел,

знак равно (N)(N + 1) / 2

знак равно ((N^2) + N) / 2

знак равно O(N^2), предполагая // do something hereвыполняется за постоянное время O(1).

——————

Также взгляните на эти

2

Источник

user17112163 28 апр '22 в 15:56

Другие вопросы по тегам algorithm time-complexity big-o

user4573247 06 авг '16 в 18:38 2016-08-06 18:38 · Accepted Answer · 2016-08-06 18:38

Вы можете использовать сигма-нотацию для расчета количества посещений внутреннего цикла ("сделайте что-нибудь здесь")

куда (*) Из правила суммирования, известного благодаря слухам, следует, что Гаусс однажды получил его на месте, будучи молодым студентом.