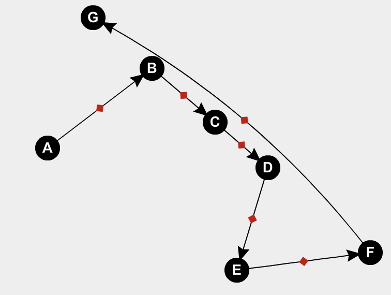
Нахождение перекрывающихся отрезков в 2D

Question

point a  = [1,0]   
point b  = [3,0]
point c  = [3,3]
point b' = [3,0]

Соединение этих точек дало бы путь линииa->b->c<-b '. Существует наложение между b к c и обратно к b` к c. Я хочу найти все перекрывающиеся пути.

Проблема, которую я пытаюсь решить, состоит в том, чтобы идентифицировать эти перекрывающиеся линии и нарисовать их в виде кривых линий, чтобы пользователь мог их различить.

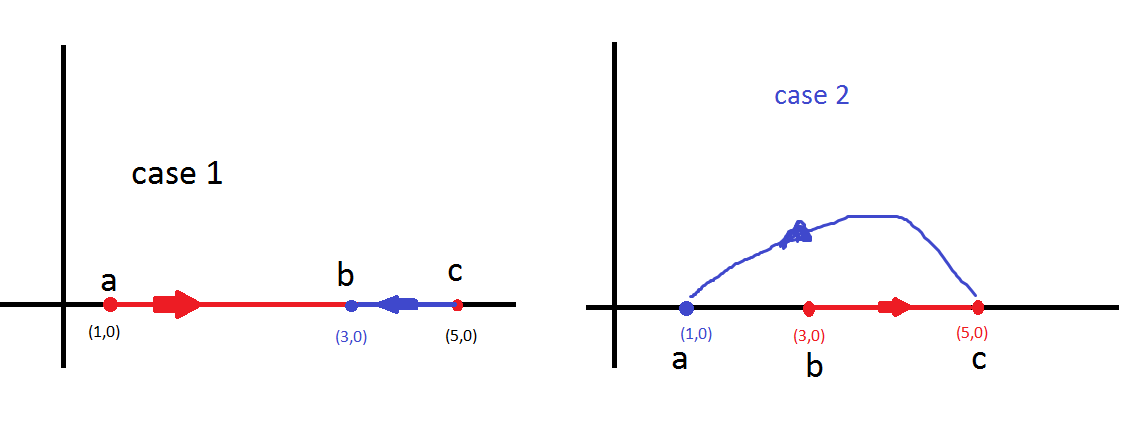
Случай 1

a = [1,0]
b = [5, 0]
c = [3, 0]

есть перекрытие, но пользователь может ясно видеть перекрытие, поэтому я игнорирую это перекрытие.

случай 2

a = [3,0]
b = [5, 0]
c = [1, 0]

Здесь, если я нарисую прямую линию, путь аб будет скрыт. Так что в этом случае нарисуйте кривую линию.

Я реализовал код, рассматривая каждую N^2 комбинацию строки и сравнивая их начало и конец по длине лат.

line AB = [ [1,0], [3,0]]
line BC = [ [3,0], [3,3]]
(AB == BC || AB == flip(BC))

Ниже приведены ссылки на код

http://jsbin.com/qibarevodi/edit?js,console

http://bl.ocks.org/d/d21a0d3e6df2cd4bb08fbe2a6e66ceb8

Есть ли более эффективный способ найти перекрывающиеся линии.

Answer 1

Предположим из ваших примеров, что вам нужно устранить визуальную неоднозначность только для одной ломаной линии: одного набора точек, соединенных отрезками. Работать с несколькими не намного сложнее, но я не буду это обсуждать.

У вас действительно есть две отдельные проблемы.

1. Определите наборы сегментов, которые лежат на одной бесконечной линии.
2. Для каждой бесконечной линии с сегментами определите те, которые должны быть представлены в виде кривых, чтобы устранить неоднозначность порядка обхода точек.

Часть 1 проста. Представьте бесконечную линию, на которой лежит каждый сегмент, в канонической форме. Затем постройте карту из канонических форм в списки (в порядке ломаных линий для последующего использования) отрезков, лежащих на них. Полезной канонической формой произвольной бесконечной линии является единичный вектор направления d и уникальная точка p это лежит ближе всего к происхождению. Это легко и быстро вычислить. Для отрезка между точками a а также b,

d = d' / length(d') where d' = [b.x - a.x, b.y - a.y]
p = d_perp (d_perp dot a) where d_perp = [d.y, -d.x]

Рассмотрение случая, когда точки находятся почти на одной линии, но не совсем, является большой дополнительной темой. Если вы заинтересованы в решениях, я могу пойти дальше.

Для части 2 мы можем рассматривать каждый набор отрезков на одной бесконечной прямой L как одномерную задачу. Похоже, вы говорите, что при трассировке ломаной линии, если какой-либо сегмент на L перезаписывает уже прослеженную вершину на L, перезаписывающий сегмент должен быть кривой. Если это определение является точным, оно напрямую приводит к простому алгоритму:

for each line L
  let S be the subset of L already traced
  for each segment a->b lying in L (in polyline order taken from the map above)
    if a in S and b in S, then
      draw a->b with a curve
    else
      draw a->b with a straight segment
      add [a->b) to S

Запись add [a->b) to S означает добавить отрезок от a в b, но исключить точку b сам. Это учитывает ваш случай 1.

Приведенный выше псевдокод довольно абстрактный. Как изобразить множество S? Возможно, самое простое - повернуть точки на оси X. Это просто, так как у вас уже есть каноническая форма для линии. Получить необходимую координату X для каждой точки p с

x = d dot p

Теперь вы можете хранить S как объединение набора 1d x-координатных интервалов. Это можно сделать довольно легко с помощью сбалансированного бинарного дерева, где ключи имеют разные интервалы. (Вам не нужно ничего более сложного, чем дерево интервалов, потому что вы храните объединение, а не перекрывающиеся интервалы.)

Дайте мне знать, если у вас возникнут проблемы с проработкой деталей. Это хорошая маленькая проблема. Например, есть крайние случаи, чтобы продумать. Что если один и тот же сегмент повторяется в пределах одной и той же ломаной? Вы не дали достаточно информации о проблеме, чтобы определить, может ли это произойти.

Answer 2

Вот что я бы сделал. Я сосредоточусь на упрощении вашей проблемы, а именно на каждой строке я буду отмечать ее как "согнутую", если она перекрывается с любой другой - перекрытия плохие. Я не собираюсь делать различия, которые вы сделали, поскольку они являются дополнительными и не упрощают. Ваши вопросы тогда по существу принимают форму:

Учитывая набор отрезков на плоскости, найдите те, которые пересекаются с другими

Если вы все еще хотите различить дела, которые вы сделали, вам нужно будет учесть, что они заказаны, и провести дополнительные проверки. Вы можете использовать дополнительную двоичную координату для их направления.

Первый вопрос: как мы храним отрезки? Похоже, вы рассматриваете их как две точки (x1,y1) и (x2,y2), поэтому вы делаете N^2 сравнений. Я бы посоветовал вам угрожать им как линиям с начальной и конечной точкой. Это означает, что мы собираемся использовать в качестве координат их наклон m, пересечение оси y, а также x1, x2. Поиск y и m не должен быть трудным. К сожалению, это не будет работать для самой оси Y. Если вы не можете быть уверены, что у вас есть сегменты на оси Y, вам может потребоваться изменить этот подход или придумать альтернативу для этого конкретного случая. Может быть, дать им специальный ключ и сохранить значения (y1,y2).

Теперь я предлагаю сохранить ваши строки в хеш-таблице (может быть, что-то вроде словаря питонов) с ключом (m,y) и содержимым списка [(x1,x2),(x1',x2'),...], Это позволяет вам для каждого сегмента проверять только те сегменты, которые лежат на одной расширенной линии. Затем вы можете пройти все свои строки один раз и отметить те, которые пересекаются с другой с тем же ключом. Не забудьте использовать быстрый тест перекрытия для этого.

Если вы хотите еще больше повысить эффективность, вы можете взглянуть на деревья интервалов. Я сам не слишком знаком с ними, но теоретически вы можете использовать эту структуру данных или ее модификацию для интервалов в списке для заданного ключа для оптимизации поиска перекрывающихся. Это будет важно, если у вас есть много шагов в одной конкретной строке. Вы можете пометить линию как изогнутую, как только она пересекается с другой в этом дереве.

Ваш алгоритм может выглядеть примерно так:

• Проецируйте отрезки линии на уклон и y-пересечение (т.е. создайте хеш-таблицу)
• Перебирайте ключи хеша
• Для каждого элемента в списке проверьте, не перекрывается ли он с другим (именно в этом случае деревья интервалов могут помочь вам ускорить дальнейшее развитие. Это также может привести к различию в вашем случае)
• Пометьте линию как "сгибаться", если чек положительный

Обращаю внимание на некоторые комментарии: использование только угла от оси x не поможет. Кроме того, запоминание направления, из которого вы пришли, не поможет, как следует осветить следующий пример.

Обратите внимание, что именно то, что вы тестируете, будет зависеть от вашего желаемого результата. Вы можете проверить на совпадение или, может быть, вы можете проверить, полностью ли содержится интервал в другом. Возможно, стоит также немного почитать о библиотеках графов и их визуализациях, поскольку ваша задача, по сути, описывает ориентированный граф с фиксированными позициями узлов. Надеюсь, что это поможет вам.