Лучший алгоритм обнаружения циклов в ориентированном графе
Каков наиболее эффективный алгоритм обнаружения всех циклов в ориентированном графе?
У меня есть ориентированный граф, представляющий расписание заданий, которые должны быть выполнены, задание - это узел, а зависимость - ребро. Мне нужно обнаружить случай ошибки цикла в этом графике, что приводит к циклическим зависимостям.
14 ответов
Алгоритм сильно связанных компонентов Тарьяна имеет O(|E| + |V|) сложность времени.
Другие алгоритмы см. В разделе Сильно связанные компоненты в Википедии.
Учитывая, что это график работ, я подозреваю, что в какой-то момент вы собираетесь отсортировать их по предлагаемому порядку выполнения.
Если это так, то реализация топологической сортировки может в любом случае обнаружить циклы. UNIX tsort конечно делает. Я думаю, что, вероятно, поэтому более эффективно обнаруживать циклы одновременно с сортировкой, а не на отдельном этапе.
Таким образом, вопрос может звучать так: "Как мне наиболее эффективно выполнять сортировку", а не "Как наиболее эффективно обнаруживать петли". На что ответ, вероятно, "использовать библиотеку", но не в том, что следующая статья в Википедии:
имеет псевдокод для одного алгоритма и краткое описание другого от Тарьяна. Как есть O(|V| + |E|) сложность времени.
Согласно лемме 22.11 Кормена и др., Введение в алгоритмы (CLRS):
Направленный граф G ацикличен тогда и только тогда, когда поиск G в глубину не дает обратных ребер.
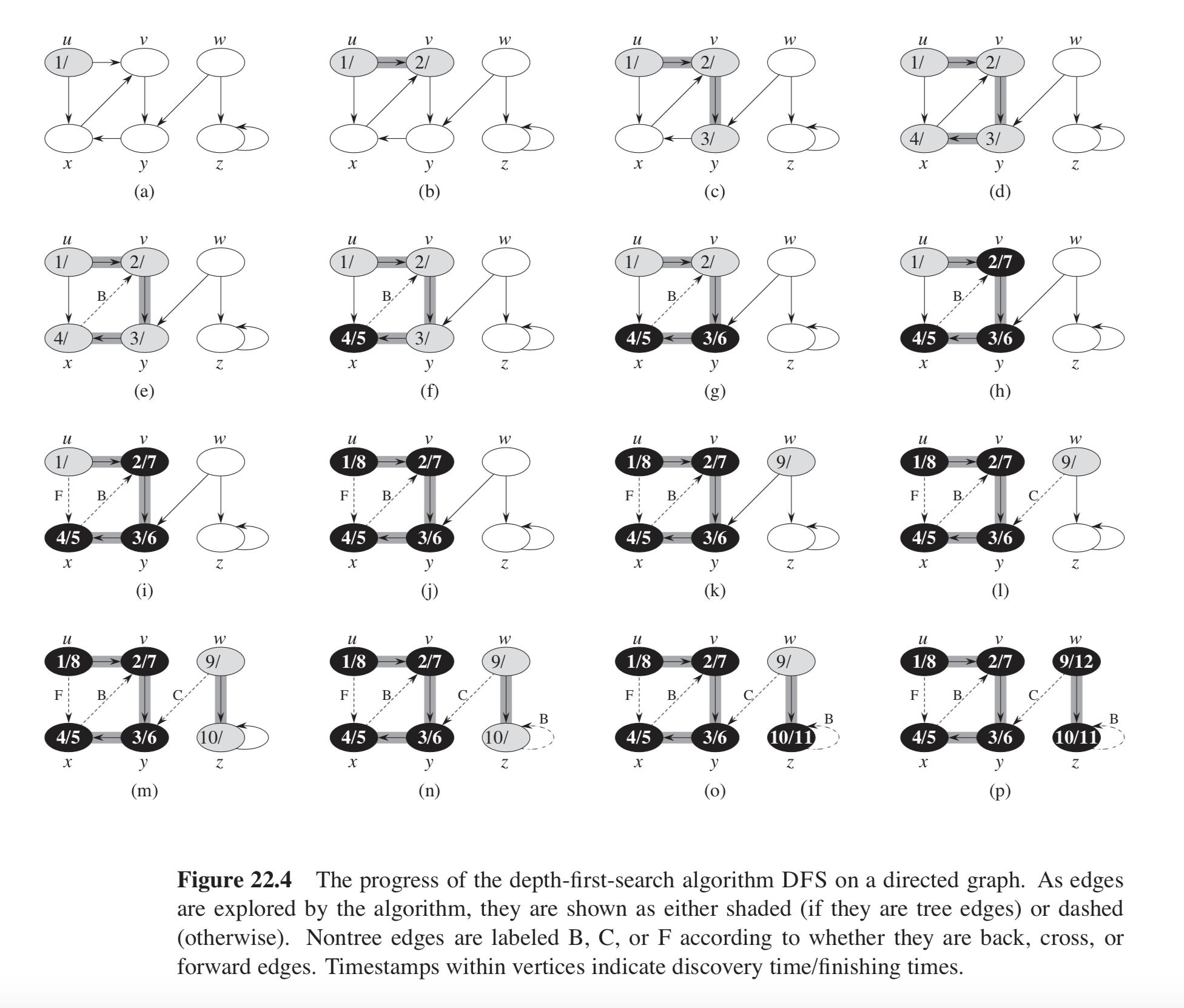
Это было упомянуто в нескольких ответах; здесь я также приведу пример кода, основанного на главе 22 CLRS. Пример графика иллюстрируется ниже.
Псевдокод CLRS для поиска в глубину гласит:
В примере на рисунке 22.4 в CLRS график состоит из двух деревьев DFS: одно состоит из узлов u, v, x и y, а другое - из узлов w и z. Каждое дерево содержит один задний край: один от x до v и другой от z до z (самоконтроль).
Ключевая реализация заключается в том, что задний край встречается, когда в DFS-VISIT функция, перебирая соседей v из u узел встречается с GRAY цвет.
Следующий код Python является адаптацией псевдокода CLRS с if добавлен пункт, который обнаруживает циклы:
import collections
class Graph(object):
def __init__(self, edges):
self.edges = edges
self.adj = Graph._build_adjacency_list(edges)
@staticmethod
def _build_adjacency_list(edges):
adj = collections.defaultdict(list)
for edge in edges:
adj[edge[0]].append(edge[1])
return adj
def dfs(G):
discovered = set()
finished = set()
for u in G.adj:
if u not in discovered and u not in finished:
discovered, finished = dfs_visit(G, u, discovered, finished)
def dfs_visit(G, u, discovered, finished):
discovered.add(u)
for v in G.adj[u]:
# Detect cycles
if v in discovered:
print(f"Cycle detected: found a back edge from {u} to {v}.")
# Recurse into DFS tree
if v not in discovered and v not in finished:
dfs_visit(G, v, discovered, finished)
discovered.remove(u)
finished.add(u)
return discovered, finished
if __name__ == "__main__":
G = Graph([
('u', 'v'),
('u', 'x'),
('v', 'y'),
('w', 'y'),
('w', 'z'),
('x', 'v'),
('y', 'x'),
('z', 'z')])
dfs(G)
Обратите внимание, что в этом примере time в CLRS псевдокод не фиксируется, потому что мы заинтересованы только в обнаружении циклов. Существует также некоторый шаблонный код для построения представления списка смежности графа из списка ребер.
Когда этот скрипт выполняется, он печатает следующий вывод:
Cycle detected: found a back edge from x to v.
Cycle detected: found a back edge from z to z.
Это именно задние края в примере в CLRS Рисунок 22.4.
Простейший способ сделать это - сделать первый проход по глубине (DFT) графа.
Если график имеет n вершины, это O(n) алгоритм временной сложности. Поскольку вам, возможно, придется делать ДПФ, начиная с каждой вершины, общая сложность становится O(n^2),
Вы должны поддерживать стек, содержащий все вершины в текущем проходе глубины, причем его первый элемент является корневым узлом. Если вы встретите элемент, который уже находится в стеке во время DFT, то у вас есть цикл.
На мой взгляд, наиболее понятным алгоритмом обнаружения цикла в ориентированном графе является алгоритм раскраски графа.
По сути, алгоритм раскраски графа обходит граф DFS (поиск в глубину вначале, что означает, что он полностью исследует путь, прежде чем исследовать другой путь). Когда он находит задний край, он помечает график как содержащий цикл.
Для более подробного объяснения алгоритма раскраски графа, пожалуйста, прочитайте эту статью: http://www.geeksforgeeks.org/detect-cycle-direct-graph-using-colors/
Также я предоставляю реализацию раскраски графов в JavaScript https://github.com/dexcodeinc/graph_algorithm.js/blob/master/graph_algorithm.js
Начните с DFS: цикл существует тогда и только тогда, когда во время DFS обнаруживается обратная сторона. Это доказано в результате теории белого пути.
Если вы не можете добавить "посещенное" свойство к узлам, используйте набор (или карту) и просто добавьте все посещенные узлы в набор, если они уже не находятся в наборе. Используйте уникальный ключ или адрес объектов в качестве "ключа".
Это также дает вам информацию о "корневом" узле циклической зависимости, которая пригодится, когда пользователь должен будет решить проблему.
Другое решение - попытаться найти следующую зависимость для выполнения. Для этого у вас должен быть какой-то стек, где вы можете вспомнить, где вы сейчас находитесь и что вам нужно делать дальше. Проверьте, есть ли зависимость в этом стеке, прежде чем выполнять ее. Если это так, вы нашли цикл.
Хотя это может показаться сложным O(N*M), вы должны помнить, что стек имеет очень ограниченную глубину (поэтому N мала) и что M становится меньше с каждой зависимостью, которую вы можете отметить как "выполненная" плюс вы можете остановить поиск, когда найдете лист (так что вам не нужно проверять каждый узел -> M тоже будет маленьким).
В MetaMake я создал график в виде списка списков, а затем удалил каждый узел, когда выполнял их, что, естественно, сократило объем поиска. На самом деле мне никогда не приходилось выполнять независимую проверку, все это происходило автоматически во время обычного выполнения.
Если вам нужен режим "только тест", просто добавьте флаг "пробного запуска", который отключает выполнение реальных заданий.
Не существует алгоритма, который мог бы найти все циклы в ориентированном графе за полиномиальное время. Предположим, у ориентированного графа есть n узлов, и каждая пара узлов имеет связи друг с другом, что означает, что у вас есть полный граф. Таким образом, любое непустое подмножество этих n узлов указывает цикл, и существует 2^n-1 число таких подмножеств. Так что никакого алгоритма полиномиального времени не существует. Итак, предположим, что у вас есть эффективный (не глупый) алгоритм, который может сообщить вам количество направленных циклов в графе, вы можете сначала найти сильные связанные компоненты, а затем применить свой алгоритм к этим связанным компонентам. Поскольку циклы существуют только внутри компонентов, а не между ними.
Я реализовал эту проблему в SML (императивное программирование) . Вот схема. Найдите все узлы, которые имеют степень или степень 0. Такие узлы не могут быть частью цикла (поэтому удалите их) . Затем удалите все входящие или исходящие ребра из таких узлов. Рекурсивно применить этот процесс к результирующему графу. Если в конце у вас не останется ни одного узла или ребра, у графа нет циклов, иначе есть.
Если DFS находит ребро, которое указывает на уже посещенную вершину, у вас есть цикл там.
https://mathoverflow.net/questions/16393/finding-a-cycle-of-fixed-length Мне нравится это решение лучше всего специально для 4 длины:)
Также физик говорит, что ты должен сделать O(V^2). Я считаю, что нам нужно только O(V)/O(V+E). Если граф связан, то DFS посетит все узлы. Если у графа есть связанные подграфы, то каждый раз, когда мы запускаем DFS на вершине этого подграфа, мы найдем связанные вершины и не будем рассматривать их для следующего запуска DFS. Поэтому возможность запуска для каждой вершины неверна.
То, как я это делаю, - это топологическая сортировка, подсчитывающая количество посещенных вершин. Если это число меньше общего количества вершин в группе обеспечения доступности баз данных, у вас есть цикл.
Как вы сказали, у вас есть набор заданий, его нужно выполнять в определенном порядке. Topological sort если вам требуется порядок для планирования заданий (или для проблем с зависимостями, если это direct acyclic graph). Бежать dfs и поддерживать список, и начать добавление узла в начале списка, и если вы встретили узел, который уже посещен. Затем вы нашли цикл в данном графике.
Если график удовлетворяет этому свойству
|e| > |v| - 1
тогда граф содержит хотя бы по циклу.