Минимальные разрушающие затраты на графике
Нам дан граф G(V,E) с N узлами (пронумерованными от 0 до N-1) и точно (N-1) двусторонними ребрами.
Каждое ребро в графе имеет положительную стоимость C (u, v)(Вес ребра).
Весь граф таков, что между любой парой узлов существует уникальный путь.
Нам также дают Список L номера узла, в котором размещена бомба.
Наша цель состоит в том, чтобы повредить / удалить край графа таким образом, чтобы после повреждения / удаления краев графа между бомбами не было связи -
то есть после повреждения нет пути между любыми двумя бомбами.
Стоимость повреждения края (u, v) = вес края (u, v).
Таким образом, мы должны повредить эти края так, чтобы общая стоимость повреждения была минимальной.
Пример:
Total Nodes=N=5
Total Bomb=Size of List L=3
List L={2,4,0}//Thats is at node number 2,4 and 0 bomb is placed...
Total Edges =N-1=4 edges are::
u v Edge-Weight
2 1 8
1 0 5
2 4 5
1 3 4
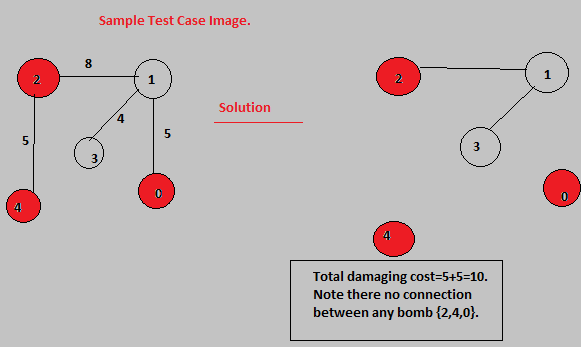
In this case the answer is ::
Total Damaging cost =(Edge Weight (2,4) + Edge Weight(0,1))
=5+5=10.
So when we remove the edge connecting node (2,4),
and the edge connecting node (0,1) ,there is no connection left
between any pair of machines in List {2,4,0};
Note any other,combinations of edges(that we damaged ) to achieve the
target goal ,needs more than 10 unit cost.
Constraints::
N(ie. Number of Nodes) <= 100,000
ListSize |L|(ie. Number of Bombs) <= N
1 <=Edge cost(u,v) <= 1000,000
Что я наделал?
До сих пор я не нашел эффективного способа:( .
Далее, так как количество узлов Nколичество ребер точно N-1 и весь граф таков, что существует уникальная траектория между любой парой узлов, и я пришел к выводу, что граф - это ДЕРЕВО.
Я пытался изменить алгоритм Крускала, но это мне тоже не помогло.
Спасибо!
6 ответов
Это проблема Multiway Cut на деревьях. Это может быть решено за полиномиальное время простым динамическим программированием. См. Чопра и Рао: " О многогранном многограннике среза", Сети 21(1):51–89, 1991.
Я думаю, что модифицированный Kruskal это путь сюда.
Возьмем граф G'=(V', E'), V'=V, E'={}. Сортируйте ребра в E в порядке возрастания стоимости. Теперь, для каждого ребра в E, добавьте его в E, если он не соединяет два компонента, у которых есть вершины с бомбами в них. Результатом является сумма затрат E-E '.
РЕДАКТИРОВАТЬ:
Выполнение этого на вашем примере.
Изначально наш набор ребер пуст {}, и мы берем ребра, отсортированные по возрастанию [(1, 2), (0, 1), (2, 4), (1, 3)]
Итак, в начале наш график состоит из 5 отключенных компонентов.
(1, 2) имеет стоимость 8, и только один из компонентов, которые он соединяет, имеет бомбу. Итак, мы добавляем его в E'. E'={(1, 2)} и у нас есть 4 компонента.
Следующим по величине преимуществом является (0, 1) со стоимостью 5. Но оба компонента имеют бомбы, поэтому не добавляйте это преимущество.
Следующий - (2, 4). Это также связано с компонентами с бомбами, поэтому мы также пропускаем это.
Наконец, самый низкий край стоимости (1, 3). Поскольку один из его компонентов (содержащий только узел 3) не имеет бомбы, мы добавляем его в E '.
Это дает нам E' = {(1,2), (1, 3)}.
Я рассуждаю так: мы пытаемся добавить ребра с более высокой стоимостью, а не с более низкой стоимостью, что гарантирует, что на любом пути между узлами с бомбами в исходном узле будут добавлены все, кроме самой низкой стоимости.
Я думаю, что это можно сделать за линейное время.
Корень дерева в некоторой вершине, а затем начните с обхода снизу вверх.
Начните с какого-нибудь листа. Если бомбы нет, отрежьте лист и двигайтесь вперед. Если есть бомба, вы должны разрезать один край на пути к этому листу. Распространите информацию о самом дешевом крае к этому листу.
Затем, когда вы находитесь во внутренней вершине, у вас есть следующие возможности: если в вершине есть бомба и несколько бомб внизу, проложите самые дешевые пути ко всем из них. Если бомбы нет и только одна бомба ниже, распространяйте информацию о самом дешевом пути. Если внизу больше бомб, разрезайте все, кроме одной с самым дорогим путем.
Вот моя гипотеза:
Граф G - это дерево. Следовательно, между любыми двумя узлами существует только один путь.
Предположим, что есть L красных (бомбовых) узлов и VL белых (не бомбовых узлов). Решение требует разбиения G на лес из L поддеревьев. Это требует удаления как минимум L-1 ребер.
Каждый из удаленных краев должен находиться на пути между двумя красными узлами.
A. Сократите дерево G, чтобы удалить все ребра, которые не участвуют в пути между двумя красными узлами.
- Удалите узлы белого листа (и край инцидента) из рассмотрения.
- Повторяйте #1 до тех пор, пока в модифицированном графе не останется белых листьев.
B. После (A) все ребра, оставленные в графе, являются ребрами, которые образуют путь между двумя красными узлами.
Выберите ребро с наименьшим весом в этом дереве. Это приведет к двум поддеревьям, каждое из которых содержит хотя бы один красный узел.
C. Вернитесь к шагу A для каждого из поддеревьев, созданных в B, если оно содержит более одного красного узла.
Это O(V log V) (|E| есть |V| -1).
Я думаю, что следующее предложение должно работать:
- 1) Начните с бомбы, в вашем примере я начинаю с:
0 - 2) Создать пути со всеми соседними узлами. Поэтому возьмите все отношения и начните путь с ними. В вашем примере это запустит один путь:
0 -> 1, - 3) Если вы ударите другую бомбу на пути, вы удалите край с наименьшей стоимостью. В примере мы не попали в бомбу, поэтому мы продолжаем с шага 2.
- 3А) Никакой бомбы пока нет. Продолжите с шага 2 и расширьте пути новыми соседними узлами. В вашем случае будет создан новый путь:
1 -> 3, А существующий будет расширен:0 -> 1 -> 2 - 3B) На пути обнаружена бомба. Пройдите по пути, где находится бомба, и уберите край с наименьшей стоимостью. В вашем примере путь
0 -> 1 -> 2содержит бомбу (2). Поэтому мы удалим связь со стоимостью 5. Удалите путь из "задачи" и перейдите к шагу 2 на последних достигнутых узлах (2 и 3).
В конце концов, вы должны пройти каждый узел ровно один раз. Если я не ошибаюсь, сложность должна быть около O(n log n)
http://www.cs.ust.hk/mjg_lib/Classes/COMP572_Fall06/Notes/Tree_Multicut.ps
имеет описание алгоритма.
Google HTML версия файла postscript
=========================================
http://dspace.mit.edu/bitstream/handle/1721.1/5394/OR-308-95.pdf?sequence=1
Случай k = 2 не является единственным полиномиально разрешимым случаем проблемы многомерного разреза. Ловдс [12] и Черкасский [3] показывают, что когда ce = 1 Ve E E и G эйлерово, то задача о многомерном разрезе полиномиально разрешима. Erdos и Sz6kely [8] показали, что обобщение задачи многомерного разреза полиномиально разрешимо, когда основной граф G является деревом. Dalhaus et. и др. [7] показали, что задача является полиномиально разрешимой для фиксированных k на плоских графах.
Вчера вечером я написал простое решение на основе жадных алгоритмов, которое заключалось в удалении узлов, которые не находятся на пути между двумя красными (терминальными) узлами, а затем в выборе узла с наименьшим весом и повторении процесса на поддеревьях. Я удалил это, так как дальнейшее чтение предположило, что проблема в NP. Но эта ссылка предполагает, что есть полиномиальное решение...