Как рассчитать энтропию файла?

Question

Как рассчитать энтропию файла? (Или давайте просто скажем кучу байтов)
У меня есть идея, но я не уверен, что она математически верна.

Моя идея заключается в следующем:

• Создайте массив из 256 целых чисел (все нули).
• Обход файла и каждого его байта,
  увеличить соответствующую позицию в массиве.
• В конце: Рассчитать "среднее" значение для массива.
• Инициализировать счетчик с нуля,
  и для каждой записи массива:
  добавить разницу записи в "среднее" к счетчику.

Ну, теперь я застрял. Как "спроецировать" результат счетчика таким образом, чтобы все результаты находились в диапазоне от 0,0 до 1,0? Но я уверен, что идея в любом случае противоречива...

Надеюсь, у кого-то есть лучшие и более простые решения?

Примечание: мне нужно все, чтобы сделать предположения о содержимом файла:
(открытый текст, разметка, сжатый или какой-то двоичный файл, ...)

Answer 1

• В конце: Рассчитать "среднее" значение для массива.
• Инициализируйте счетчик с нулем, и для каждой записи массива: добавьте разницу записи в "среднее" к счетчику.

С некоторыми изменениями вы можете получить энтропию Шеннона:

переименуйте "среднее" в "энтропию"

(float) entropy = 0
for i in the array[256]:Counts do 
  (float)p = Counts[i] / filesize
  if (p > 0) entropy = entropy - p*lg(p) // lgN is the logarithm with base 2

Редактировать: как упомянул Уэсли, мы должны разделить энтропию на 8, чтобы отрегулировать ее в диапазоне 0 . , 1 (или в качестве альтернативы мы можем использовать логарифмическое основание 256).

Answer 2

Более простое решение: сжать файл. Используйте соотношение размеров файлов: (размер-gzipped)/(размер-оригинал) в качестве меры случайности (то есть энтропии).

Этот метод не дает точного абсолютного значения энтропии (поскольку gzip не является "идеальным" компрессором), но он достаточно хорош, если вам нужно сравнивать энтропию разных источников.

Answer 3

Чтобы вычислить информационную энтропию набора байтов, вам нужно сделать что-то похожее на ответ Тыдока. (Ответ Тыдока работает над набором битов.)

Предполагается, что следующие переменные уже существуют:

• byte_counts 256-элементный список количества байтов с каждым значением в вашем файле. Например, byte_counts[2] это число байтов, которые имеют значение 2,

• total это общее количество байтов в вашем файле.

Я напишу следующий код на Python, но должно быть очевидно, что происходит.

import math

entropy = 0

for count in byte_counts:
    # If no bytes of this value were seen in the value, it doesn't affect
    # the entropy of the file.
    if count == 0:
        continue
    # p is the probability of seeing this byte in the file, as a floating-
    # point number
    p = 1.0 * count / total
    entropy -= p * math.log(p, 256)

Есть несколько вещей, которые важно отметить.

• Чек для count == 0 это не просто оптимизация. Если count == 0, затем p == 0и log (p) будет неопределенным ("отрицательная бесконечность"), что приведет к ошибке.

• 256 в призыве к math.log представляет количество дискретных значений, которые возможны. Байт, состоящий из восьми битов, будет иметь 256 возможных значений.

Результирующее значение будет находиться в диапазоне от 0 (все байты в файле одинаковы) до 1 (байты равномерно распределены между всеми возможными значениями байта).

---

Объяснение использования базы журнала 256

Это правда, что этот алгоритм обычно применяется с использованием базы журнала 2. Это дает полученный ответ в битах. В таком случае у вас есть максимум 8 бит энтропии для любого данного файла. Попробуйте сами: максимизируйте энтропию ввода, сделав byte_counts список всех 1 или же 2 или же 100, Когда байты файла распределены равномерно, вы обнаружите, что энтропия составляет 8 битов.

Можно использовать другие логарифмические базы. Использование b= 2 позволяет получить результат в битах, поскольку каждый бит может иметь 2 значения. При использовании b= 10 результат помещается в дитах или десятичных битах, поскольку для каждого дита имеется 10 возможных значений. Использование b= 256 даст результат в байтах, поскольку каждый байт может иметь одно из 256 дискретных значений.

Интересно, что используя идентификаторы логов, вы можете решить, как преобразовать полученную энтропию между единицами. Любой результат, полученный в единицах битов, может быть преобразован в единицы байтов путем деления на 8. Как интересный, преднамеренный побочный эффект, это дает энтропию как значение между 0 и 1.

В итоге:

• Вы можете использовать различные единицы для выражения энтропии
• Большинство людей выражают энтропию в битах (b= 2)
  • Для набора байтов это дает максимальную энтропию 8 бит
  • Поскольку запрашивающий хочет получить результат от 0 до 1, разделите этот результат на 8 для значимого значения
• Приведенный выше алгоритм вычисляет энтропию в байтах (b= 256)
  • Это эквивалентно (энтропия в битах) / 8
  • Это уже дает значение от 0 до 1

Answer 4

Я опоздал с ответом на два года, поэтому, пожалуйста, учтите это, несмотря на то, что проголосовали только несколько голосов.

Краткий ответ: используйте мои 1-е и 3-е полужирное уравнение ниже, чтобы понять, о чем думает большинство людей, когда они говорят "энтропия" файла в битах. Используйте только 1-е уравнение, если вы хотите энтропию Шеннона H, которая на самом деле является энтропией / символом, как он сказал 13 раз в своей статье, о которой большинство людей не знают. Некоторые онлайн-калькуляторы энтропии используют этот, но H Шеннона - это "специфическая энтропия", а не "полная энтропия", которая вызывает столько путаницы. Используйте 1-е и 2-е уравнение, если вы хотите получить ответ между 0 и 1, который является нормализованной энтропией / символом (это не биты / символ, а истинная статистическая мера "энтропийной природы" данных, позволяя данным выбирать свою собственную базу журналов вместо произвольного присвоения 2, е или 10).

Существует 4 типа энтропии файлов (данных) длиной N символов с n уникальными типами символов. Но имейте в виду, что, зная содержимое файла, вы знаете его состояние и, следовательно, S=0. Если быть точным, если у вас есть источник, который генерирует много данных, к которым у вас есть доступ, то вы можете рассчитать ожидаемую будущую энтропию / характер этого источника. Если вы используете следующее для файла, более правильно будет сказать, что он оценивает ожидаемую энтропию других файлов из этого источника.

• Энтропия Шеннона (специфическая) H = -1*sum(count_i / N * log(count_i / N))
  где count_i - количество символов, которое я встретил в N.
  Единицы - биты / символ, если log - основание 2, нац / символ, если натуральный лог.
• Нормализованная удельная энтропия: H / log(n)
  Единицы энтропии / символа. Диапазон от 0 до 1. 1 означает, что каждый символ встречался одинаково часто, а около 0 все символы, кроме 1, встречались только один раз, а остальная часть очень длинного файла была другим символом. Журнал находится в той же базе, что и H.
• Абсолютная энтропия S = N * H
  Единицы - это биты, если log - это база 2, nats - если ln())
• Нормализованная абсолютная энтропия S = N * H / log(n)
  Единица "энтропия", варьируется от 0 до N. Лог находится в той же базе, что и H.

Хотя последняя является истинной "энтропией", первая (энтропия Шеннона H) - это то, что все книги называют "энтропией" без (необходимого ИМХО) квалификации. Большинство не уточняет (как это сделал Шеннон), что это бит / символ или энтропия на символ. Называть H "энтропией" - это слишком свободно.

Для файлов с одинаковой частотой каждого символа: S = N * H = N. Это касается большинства больших файлов битов. Энтропия не выполняет никакого сжатия данных и, таким образом, полностью игнорирует любые шаблоны, поэтому 000000111111 имеет те же H и S, что и 010111101000 (6 1 и 6 0 в обоих случаях).

Как уже говорили другие, использование стандартной процедуры сжатия, такой как gzip и деление до и после, даст лучшую меру количества ранее существовавшего "порядка" в файле, но это смещено по отношению к данным, которые лучше соответствуют схеме сжатия. Не существует полностью оптимизированного компрессора общего назначения, который мы могли бы использовать для определения абсолютного "порядка".

Еще одна вещь, которую следует учитывать: H меняется, если вы меняете способ выражения данных. H будет другим, если вы выберете разные группы битов (биты, кусочки, байты или шестнадцатеричные значения). Таким образом, вы делите на log(n), где n - количество уникальных символов в данных (2 для двоичного, 256 для байтов), а H будет варьироваться от 0 до 1 (это нормализованная интенсивная энтропия Шеннона в единицах энтропии на символ), Но технически, если встречается только 100 из 256 типов байтов, тогда n=100, а не 256.

H представляет собой "интенсивную" энтропию, то есть для каждого символа она аналогична конкретной энтропии в физике, которая представляет собой энтропию на кг или на моль. Обычная "обширная" энтропия файла, аналогичного физике S, равна S = N * H, где N - количество символов в файле. H будет в точности аналогична части идеального объема газа. Информационная энтропия не может быть просто сделана точно равной физической энтропии в более глубоком смысле, потому что физическая энтропия допускает "упорядоченные", а также неупорядоченные схемы: физическая энтропия получается больше, чем полностью случайная энтропия (такая как сжатый файл). Один аспект отличается Для идеального газа есть дополнительный фактор 5/2 для учета этого: S = k * N * (H+5/2) где H = возможные квантовые состояния на молекулу = (xp)^3/hbar * 2 * sigma^2 где x= ширина прямоугольника, p= общий ненаправленный импульс в системе (рассчитанный по кинетической энергии и массе на молекулу) и sigma=0,341 в соответствии с принципом неопределенности, дающим только число возможные состояния в пределах 1-го уровня

Небольшая математика дает более короткую форму нормализованной обширной энтропии для файла:

S = N * H / log(n) = сумма (count_i*log(N/count_i))/log(n)

Единицами этого являются "энтропия" (которая на самом деле не единица). Нормализовано, чтобы быть лучшей универсальной мерой, чем "энтропийные" единицы N * H. Но это также не следует называть "энтропией" без пояснения, потому что нормальное историческое соглашение состоит в том, чтобы ошибочно называть H "энтропией" (что противоречит пояснения, сделанные в тексте Шеннона).

Answer 5

Для чего это стоит, вот традиционный (биты энтропии) вычисления, представленные в C#

/// <summary>
/// returns bits of entropy represented in a given string, per 
/// http://en.wikipedia.org/wiki/Entropy_(information_theory) 
/// </summary>
public static double ShannonEntropy(string s)
{
    var map = new Dictionary<char, int>();
    foreach (char c in s)
    {
        if (!map.ContainsKey(c))
            map.Add(c, 1);
        else
            map[c] += 1;
    }

    double result = 0.0;
    int len = s.Length;
    foreach (var item in map)
    {
        var frequency = (double)item.Value / len;
        result -= frequency * (Math.Log(frequency) / Math.Log(2));
    }

    return result;
}

Answer 6

Это то, что ent мог справиться? (Или, возможно, его нет на вашей платформе.)

$ dd if=/dev/urandom of=file bs=1024 count=10
$ ent file
Entropy = 7.983185 bits per byte.
...

В качестве встречного примера приведу файл без энтропии.

$ dd if=/dev/zero of=file bs=1024 count=10
$ ent file
Entropy = 0.000000 bits per byte.
...

Answer 7

Нет такой вещи как энтропия файла. В теории информации энтропия является функцией случайной величины, а не фиксированного набора данных (ну, технически фиксированный набор данных имеет энтропию, но эта энтропия будет равна 0 - мы можем рассматривать данные как случайное распределение, которое имеет только один возможный исход с вероятностью 1).

Чтобы рассчитать энтропию, вам нужна случайная величина, с помощью которой можно смоделировать ваш файл. Тогда энтропия будет энтропией распределения этой случайной величины. Эта энтропия будет равна количеству битов информации, содержащейся в этой случайной переменной.

Answer 8

Если вы используете энтропию теории информации, имейте в виду, что может не иметь смысла использовать ее в байтах. Скажем, если ваши данные состоят из чисел с плавающей точкой, вы должны вместо этого подобрать распределение вероятностей для этих чисел и вычислить энтропию этого распределения.

Или, если содержимое файла содержит символы Юникода, вы должны использовать их и т. Д.

Answer 9

Re: Мне нужно все, чтобы сделать предположения о содержимом файла: (открытый текст, разметка, сжатый или какой-то двоичный файл, ...)

Как уже отмечали другие (или были сбиты с толку / отвлечены), я думаю, что вы на самом деле говорите о метрической энтропии (энтропия, деленная на длину сообщения). См. Больше в Энтропии (теория информации) - Wikipedia.

Комментарий джиттера, связанный с сканированием данных на предмет аномалий энтропии, очень важен для вашей основной цели. Это в конечном итоге связано с libdisorder (C библиотека для измерения байтовой энтропии). Этот подход, по-видимому, даст вам гораздо больше информации для работы, так как он показывает, как меняется метрическая энтропия в разных частях файла. Посмотрите, например, этот график того, как изменяется энтропия блока из 256 последовательных байтов изображения JPG размером 4 МБ (ось Y) для различных смещений (ось X). В начале и в конце энтропия ниже, так как она частично заполнена, но для большей части файла она составляет около 7 бит на байт.

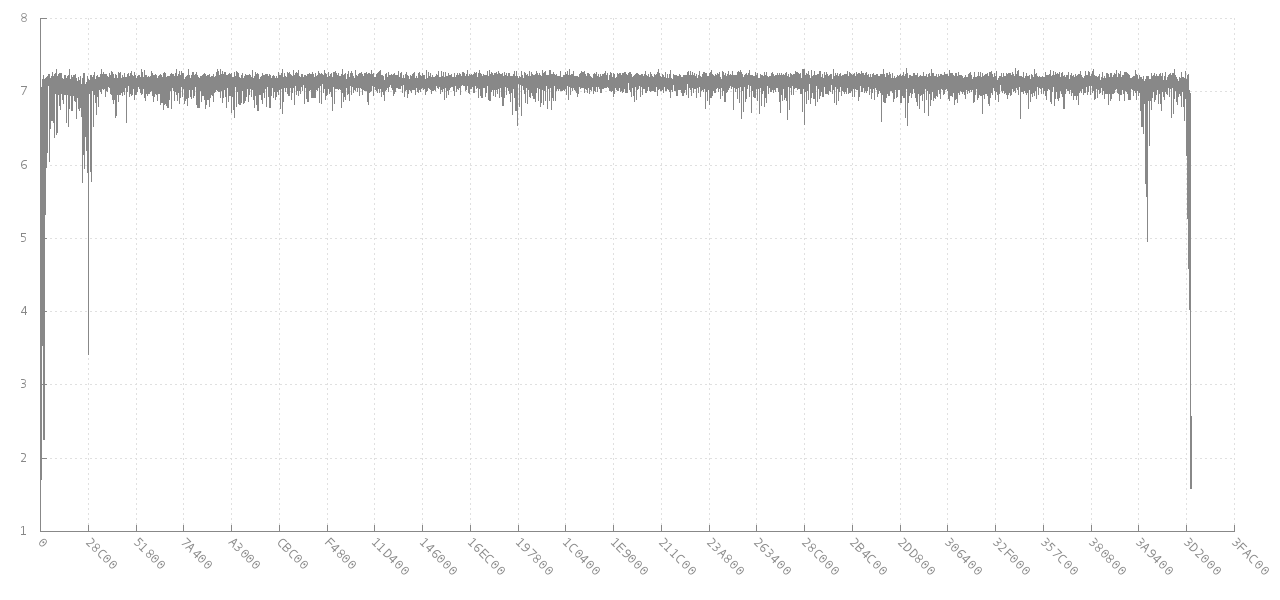Источник: https://github.com/cyphunk/entropy_examples. [ Обратите внимание, что этот и другие графики доступны через новую лицензию http://nonwhiteheterosexualmalelicense.org/.... ]

Более интересным является анализ и аналогичные графики при анализе байтовой энтропии отформатированного диска FAT | GL.IB.LY

Такие статистические данные, как максимальное, минимальное, режимное и стандартное отклонение метрической энтропии для всего файла и / или первого и последнего его блоков, могут быть очень полезны в качестве сигнатуры.

Эта книга также кажется актуальной: обнаружение и распознавание маскировки файлов для электронной почты и защиты данных - Springer

Answer 10

Вычисляет энтропию любой строки беззнаковых символов размера "длина". Это в основном рефакторинг кода, который можно найти по адресу http://rosettacode.org/wiki/Entropy. Я использую это для 64-битного генератора IV, который создает контейнер из 100000000 IV без дупликов и средней энтропии 3,9. http://www.quantifiedtechnologies.com/Programming.html

#include <string>
#include <map>
#include <algorithm>
#include <cmath>
typedef unsigned char uint8;

double Calculate(uint8 * input, int  length)
  {
  std::map<char, int> frequencies;
  for (int i = 0; i < length; ++i)
    frequencies[input[i]] ++;

  double infocontent = 0;
  for (std::pair<char, int> p : frequencies)
  {
    double freq = static_cast<double>(p.second) / length;
    infocontent += freq * log2(freq);
  }
  infocontent *= -1;
  return infocontent;
 }

Answer 11

Вот алгоритм Java, основанный на этом фрагменте и вторжении, которое произошло во время войны бесконечности.

       public static double shannon_entropy(File file) throws IOException {
        byte[] bytes= Files.readAllBytes(file.toPath());//byte sequence
        int max_byte = 255;//max byte value
        int no_bytes = bytes.length;//file length
        int[] freq = new int[256];//byte frequencies
        for (int j = 0; j < no_bytes; j++) {
            int value = bytes[j] & 0xFF;//integer value of byte
            freq[value]++;
        }
        double entropy = 0.0;
        for (int i = 0; i <= max_byte; i++) {
            double p = 1.0 * freq[i] / no_bytes;
            if (freq[i] > 0)
                entropy -= p * Math.log(p) / Math.log(2);
        }
       return entropy;
    }

usage-example:

       File file=new File("C:\\Users\\Somewhere\\In\\The\\Omniverse\\Thanos Invasion.Log");
 int file_length=(int)file.length();
 double shannon_entropy=shannon_entropy(file);
 System.out.println("file length: "+file_length+" bytes");
 System.out.println("shannon entropy: "+shannon_entropy+" nats i.e. a minimum of "+shannon_entropy+" bits can be used to encode each byte transfer" +
                    "\nfrom the file so that in total we transfer atleast "+(file_length*shannon_entropy)+" bits ("+((file_length*shannon_entropy)/8D)+
                    " bytes instead of "+file_length+" bytes).");

output-example:

длина файла: 5412 байтов

энтропия Шеннона: 4,537883805240875 натс, т.е. для кодирования каждой передачи байта из файла может быть использовано минимум 4,537883805240875 бит, так что в целом мы передаем как минимум 24559,027153963616 бит (3069,878394245452 байта вместо 5412 байтов).

Answer 12

Без какой-либо дополнительной информации энтропия файла равна (по определению) его размеру *8 бит. Энтропия текстового файла примерно равна 6,6 битам, учитывая, что:

• каждый персонаж одинаково вероятен
• в байте 95 печатных символов
• log(95)/log(2) = 6,6

Энтропия текстового файла на английском языке оценивается в пределах от 0,6 до 1,3 бит на символ (как описано здесь).

В общем, вы не можете говорить об энтропии данного файла. Энтропия - это свойство набора файлов.

Если вам нужна энтропия (или, если быть точным, энтропия на байт), лучший способ - сжать ее с помощью gzip, bz2, rar или любого другого сильного сжатия, а затем разделить сжатый размер на несжатый размер. Это было бы отличной оценкой энтропии.

Вычисление энтропийного байта за байтом, как предположил Ник Дандулакис, дает очень плохую оценку, поскольку предполагает, что каждый байт независим. Например, в текстовых файлах гораздо более вероятно иметь маленькую букву после буквы, чем пробел или пунктуацию после буквы, поскольку слова обычно длиннее 2 символов. Таким образом, вероятность того, что следующий символ окажется в диапазоне z, коррелирует со значением предыдущего символа. Не используйте грубую оценку Ника для каких-либо реальных данных, вместо этого используйте коэффициент сжатия gzip.