Чтобы убедиться: лемма прокачки только для бесконечных регулярных языков?

Question

Так что речь идет не о лемме прокачки, а о том, как она работает, а о предварительном условии.

Везде в сети вы можете прочитать, что обычные языки должны проходить прокачивающую лемму, но теперь никто не говорит о конечных языках, которые на самом деле являются частью обычных языков.

Таким образом, мы все можем согласиться с тем, что следующий язык является конечным языком, а также является обычным, но он определенно не проходит накачивающую лемму:

L = {'abc', 'defghi'}

Пожалуйста, скажите мне, если просто никто не пишет об этом или почему мы не правы - или даже нет.

Answer 1

Причина, по которой конечные языки работают с леммой прокачки, заключается в том, что вы можете сделать длину прокачки длиннее, чем самое длинное слово в языке. Насосная лемма, как сказано в Википедии (у меня нет с собой книги по теории вычислений):

Пусть L обычный язык. Тогда существует целое число p ≥ 1, зависящее только от L, так что каждая строка w в L длиной не менее p (p называется "длиной накачки") может быть записана как w = xyz (т. Е. W можно разделить на три подстроки), удовлетворяющих следующим условиям:

1. | у | ≥ 1
2. | ху | ≤ р
3. для всех i ≥ 0, xy ⁱ z ∈ L

Теперь рассмотрим некоторый конечный язык L и пусть k = max _{w ∈ L} | ш | быть длиной самого длинного слова в L. Тогда я утверждаю, что минимальная длина накачки для L равна p = k +1. Поскольку в L нет слов с длиной не менее k +1, (безрезультатно) верно, что каждое такое слово удовлетворяет трем условиям (или, в действительности, любому другому условию, которое вы хотите задать).

Конечно, вы можете видеть, что любой конечный язык является регулярным (обычные языки закрыты при конечном объединении, и все языки одного слова являются регулярными), но обратите внимание, что этот аргумент не показывает этого; важно помнить, что хотя любой обычный язык может быть прокачан, существуют языки, которые можно прокачать, но они не являются регулярными.

Answer 2

"В КОНТЕКСТЕ НАСОСА ЛЕММЫ ДЛЯ РЕГУЛЯРНЫХ ЯЗЫКОВ"

Да, мы согласны, все конечные языки являются регулярными языками, что означает, что мы можем иметь конечные автоматы, а также регулярные выражения для любого конечного языка
В то время как a infinite language may be regular or not, Диаграмма Венна показана ниже. Так что нам нужно проверять только бесконечный язык L, где его регулярность отсутствует!

Подумайте о ФА:

• любой automata за a finite language can not contains loop! (также regular expressions for finite language will be without * and +операция).

• любой automata за a infinite language(regular) will contain the loop, We can't construct an automata for infinite language without loop; где цикл может быть собственным циклом через какое-то другое состояние. {Если его цикл сам, то один символ повторяется любое количество раз, если через другое состояние последовательность символов входит в цикл, может повторяться любое число раз}.

Накачка означает повторение. В прокачке леммы w можно разбить на три части x, y, z. "У" является частью w происходит в цикле (это у>=1). Так что прокачка леммы ничего не находит зацикливая часть y и повторяя эту часть цикла любое количество раз.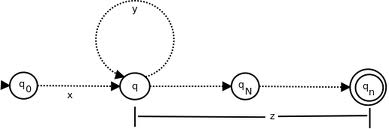
Вы можете увидеть, если вы повторяете цикл любое количество раз и генерируете новую строку w' все еще на языке.

ПРИМЕЧАНИЕ: Regular Expressions for infinite language can't be without * and +работа!

[ответ] В автоматах нет цикла для конечного языка, поэтому мы не можем качать (генерировать, повторяя) новые строки в языке. А Лемма прокачки неприменима для конечного языка.

Хотя некоторые авторы также объясняют прокачку леммы для конечного языка, где i в xyⁱ z можно повторять ограниченно (скажем, k ≤ i ≤ m)

---

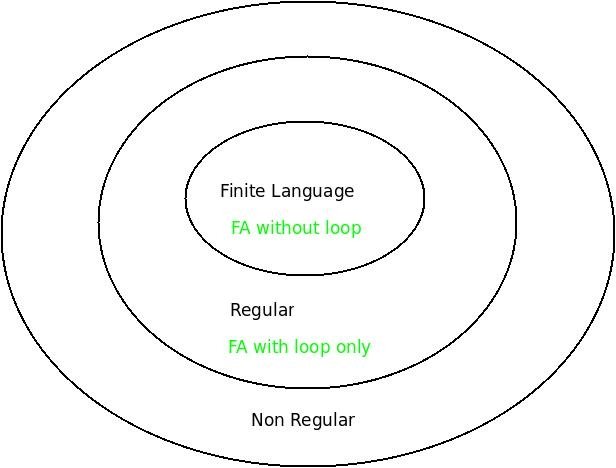
В диаграмме Венна каждое конечное множество регулярно. Бесконечный набор может быть регулярным или нет. Regular-Languages ⊆ Non-Regular Languages

---

Answer 3

Есть самый простой способ показать, что какой-то язык бесконечен. Предположим, что L является языком для некоторого регулярного выражения E, L(E).

Предположим, что L (E) эквивалентно {ab^nc | n ≥ 0},

Мы знаем, что E находится в форме ab*cи мы знаем, что этот язык, вероятно, является регулярным (мы не можем доказать, что что-то является регулярным), поскольку из леммы прокачки этот вывод k = 0поставить по-другому, xz = acи каждое регулярное выражение имеет эквивалентный автомат.

Вывод прост: если DFA имеет какое-то состояние с переходом к себе, язык бесконечен.

     a   b   c

 q0  q1    
 q1     q1  q2
*q2         

q1 имеет переход к себе, поэтому L (E) бесконечно.

Answer 4

Конечные языки являются регулярными языками по определению, потому что вы можете создать регулярное выражение, которое удовлетворяет его, просто выражая объединение всех слов (например, (abc)|(defghi) является регулярным выражением, которое удовлетворяет вашему языку), и, следовательно, вы можете иметь детерминированный конечный автомат, который удовлетворяет ему.

Неспособность пройти накачанную лемму не означает, что язык не является регулярным. Фактически, чтобы использовать лемму прокачки, ваш язык должен иметь своего рода замыкание в своем определении. Если ваш язык - это просто набор слов, то нечего в нем "прокачивать".