Визуализация ближайших соседних зон
Я пишу приложение, которое ищет точки в двухмерном пространстве, используя дерево kd. Во время разработки было бы хорошо иметь возможность "видеть" зоны ближайших соседей, окружающих каждую точку.
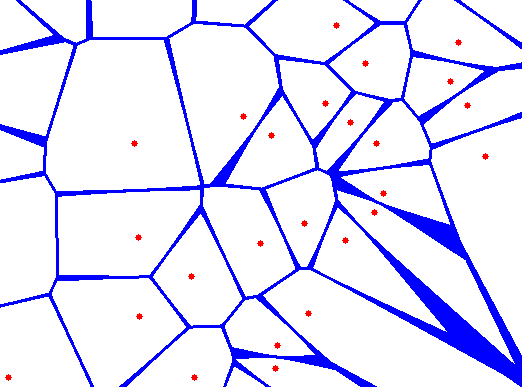
На прилагаемом изображении красные точки - это точки в дереве kd, а синие линии, окружающие каждую точку, ограничивают зону, в которой поиск ближайшего соседа вернет содержащуюся точку.
Изображение было создано таким образом:
for each point in the space:
da = distance to nearest neighbor
db = distance to second-nearest neighbor
if absolute_value(da - db) < 4:
draw blue pixel
Этот алгоритм имеет две проблемы:
- (более важно) Это медленно на моем (достаточно быстром Core i7) компьютере.
- (менее важно) Это неряшливо, как вы можете видеть по разной ширине синих линий.
Как называется эта "визуализация" набора точек?
Какие есть хорошие алгоритмы для создания такой визуализации?
4 ответа
Это называется диаграммой Вороного, и существует множество отличных алгоритмов для их эффективной генерации. Больше всего я слышал об алгоритме Fortune, который работает за время O(n log n), хотя для этой проблемы существуют и другие алгоритмы.
Надеюсь это поможет!
Иаков,
эй, вы нашли интересный способ генерации этой диаграммы Вороного, хотя она не так эффективна.
Прежде всего, менее важная проблема: границы различной толщины, которые вы получаете, эти формы бабочки, на самом деле являются областью между двумя ветвями гиперболы. Именно гипербола определяется уравнением |da - db| = 4. Чтобы получить толстую линию вместо этого, вы должны изменить этот критерий и заменить его расстоянием до биссектрисы двух ближайших соседей, пусть A и B; используя векторное исчисление, | PA.AB/||AB|| - ||AB||/2 | < 4.
Более важный вопрос: есть два хорошо известных эффективных решения для построения диаграммы Вороного набора точек: алгоритм развертки Fortune (как упомянуто templatetypedef) и решения "Разделяй и властвуй" от Preparata & Shamos. Оба работают в оптимальное время O(N.Lg(N)) для N точек, но их не так просто реализовать.
Этот алгоритм будет строить диаграмму Вороного в виде набора отрезков и полулиний. Проверьте http://en.wikipedia.org/wiki/Voronoi_diagram.
В этой статье "Примитивы для манипулирования общими подразделениями и вычисления Вороного" описываются оба алгоритма с использованием несколько высокоуровневой структуры, заботящейся обо всех деталях реализации; статья сложная, но алгоритмы реализуемы.
Вы также можете взглянуть на "Простой итеративный алгоритм для плоской диаграммы Вороного", который я никогда не пробовал.
Совершенно другой подход состоит в том, чтобы напрямую построить карту расстояний из заданных точек, например, с помощью алгоритма Дейкстры: начиная с заданных точек, вы увеличиваете границу области на заданном расстоянии от каждой точки и прекращаете расти, когда две границы встретить. [Требуются дополнительные пояснения.] См. http://1.bp.blogspot.com/-O6rXggLa9fE/TnAwz4f9hXI/AAAAAAAAAPk/0vrqEKRPVIw/s1600/distmap-20-seed4-fin.jpg
Другой хорошей отправной точкой (для эффективного вычисления карты расстояний) может быть "Общий алгоритм вычисления преобразований расстояния в линейном времени".
Из личного опыта: алгоритм Fortune - это боль в реализации. Алгоритм "разделяй и властвуй", представленный Гибасом и Столфи, не так уж и плох; они дают подробный псевдокод, который легко транскрибировать на процедурный язык программирования. И то и другое взорвется, если у вас будут почти вырожденные входы и вы используете числа с плавающей запятой, но поскольку примитивы являются квадратичными, если вы можете представлять координаты как 32-битные целые числа, то вы можете использовать 64-битные вычисления для выполнения определителей.
Как только вы это заработаете, вы можете подумать о замене алгоритмов дерева kd, которые имеют наихудший случай тета (√n), алгоритмами, работающими на плоских подразделениях.
Вы можете найти отличную реализацию для этого в библиотеке D3.js: http://mbostock.github.com/d3/ex/voronoi.html