Emmeans непрерывная независимая переменная
Я хочу объяснить Type_f с Type_space эксперимента и скорость Exhaustion_product и количественная переменная Age,
Вот мои данные:
res=structure(list(Type_space = structure(c(2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L), .Label = c("",
"29-v1", "29-v2", "88-v1", "88-v2"), class = "factor"), Id = c(1L,
2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 13L, 14L, 15L,
16L, 17L, 18L, 19L, 20L, 21L, 22L, 23L, 24L, 25L, 26L, 27L, 28L,
29L, 30L, 31L, 32L, 33L, 34L, 35L, 36L, 37L, 38L, 39L, 40L, 41L,
42L, 43L, 44L, 45L, 46L, 47L, 48L, 49L, 50L, 51L, 52L, 53L, 54L,
55L, 56L, 57L, 58L, 59L, 60L, 61L, 62L, 63L, 64L, 65L, 66L, 67L,
68L, 69L, 70L, 71L, 72L, 73L, 74L, 75L, 76L, 77L, 78L, 79L, 80L,
81L, 82L, 1L, 2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L,
13L, 14L, 15L, 16L, 17L, 18L, 19L, 20L, 21L, 22L, 23L, 24L, 25L,
26L, 27L, 28L, 29L, 30L, 31L, 32L, 33L, 34L, 35L, 36L, 37L, 38L,
39L, 40L, 41L, 42L, 43L, 44L, 45L, 46L, 47L, 48L, 49L, 50L, 51L,
52L, 53L, 54L, 55L, 56L, 57L, 58L, 59L, 60L, 61L, 62L, 63L, 64L,
65L, 66L, 67L, 68L, 69L, 70L, 71L, 72L, 73L, 74L, 75L, 76L, 77L,
78L, 79L, 80L, 81L, 82L, 83L, 84L, 85L, 86L, 87L, 88L, 89L, 90L,
91L, 92L, 93L, 94L, 95L, 96L, 97L, 98L, 99L, 100L, 101L, 102L,
103L, 104L, 105L, 106L, 107L, 108L, 109L, 110L, 111L, 112L, 113L,
114L, 115L, 116L, 117L, 118L, 119L, 120L, 121L, 122L, 123L, 124L,
125L, 126L, 127L, 128L, 129L, 130L, 131L, 132L, 133L, 134L, 135L,
136L, 137L, 138L, 139L, 140L, 141L, 142L, 143L, 144L, 145L, 146L,
147L, 148L, 149L, 150L, 151L, 152L, 153L, 154L, 155L, 156L, 157L,
158L, 159L, 160L, 161L, 162L, 163L, 164L, 165L, 166L, 167L, 1L,
2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 13L, 14L, 15L,
16L, 17L, 18L, 19L, 20L, 21L, 22L, 23L, 24L, 25L, 26L, 27L, 28L,
29L, 30L, 31L, 32L, 33L, 34L, 35L, 36L, 37L, 38L, 39L, 40L, 41L,
42L, 43L, 44L, 45L, 46L, 47L, 48L, 49L, 50L, 51L, 52L, 53L, 54L,
55L, 56L, 57L, 58L, 59L, 60L, 61L, 62L, 63L, 64L, 65L, 66L, 67L,
68L, 69L, 70L, 71L, 72L, 73L, 74L, 75L, 76L, 77L, 78L, 79L, 80L,
81L, 82L, 83L, 84L, 85L, 86L, 87L, 88L, 89L, 90L, 91L, 92L, 93L,
94L, 95L, 96L, 97L, 98L, 99L, 100L, 101L, 102L, 103L, 1L, 2L,
3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 13L, 14L, 15L, 16L,
17L, 18L, 19L, 20L, 21L, 22L, 23L, 24L, 25L, 26L, 27L, 28L, 29L,
30L, 31L, 32L, 33L, 34L, 35L, 36L, 37L, 38L, 39L, 40L, 41L, 42L,
43L, 44L, 45L, 46L, 47L, 48L, 49L, 50L, 51L, 52L, 53L, 54L, 55L,
56L, 57L, 58L, 59L, 60L, 61L, 62L, 63L, 64L, 65L, 66L, 67L, 68L,
69L, 70L, 71L, 72L, 73L, 74L, 75L, 76L, 77L, 78L, 79L, 80L, 81L,
82L, 83L, 84L, 85L, 86L, 87L, 88L, 89L, 90L, 91L, 92L, 93L, 94L,
95L, 96L, 97L, 98L, 99L, 100L, 101L, 102L, 103L, 104L, 105L,
106L, 107L, 108L, 109L, 110L, 111L, 112L, 113L, 114L, 115L, 116L,
117L, 118L, 119L, 120L, 121L, 122L, 123L, 124L, 125L, 126L, 127L,
128L, 129L, 130L, 131L, 132L, 133L, 134L, 135L, 136L, 137L, 138L,
139L, 140L, 141L, 142L, 143L, 144L, 145L, 146L, 147L, 148L, 149L,
150L, 151L, 152L, 153L, 154L, 155L, 156L, 157L, 158L, 159L, 160L,
161L, 162L, 163L, 164L), Age = c(3, 10, 1, 5, 4, 2, 1, 8, 2,
13, 1, 6, 3, 5, 2, 1, 3, 8, 3, 6, 1, 3, 7, 1, 2, 2, 2, 1, 2,
5, 4, 1, 6, 3, 6, 8, 2, 3, 4, 7, 3, 2, 6, 2, 3, 7, 1, 5, 4, 1,
4, 3, 2, 3, 5, 5, 2, 1, 1, 5, 8, 7, 2, 2, 4, 3, 4, 4, 2, 2, 10,
7, 5, 3, 3, 5, 7, 5, 3, 4, 5, 4, 1, 8, 6, 1, 12, 1, 6, 3, 4,
4, 13, 5, 2, 7, 7, 20, 1, 1, 1, 7, 1, 4, 3, 8, 2, 2, 4, 1, 1,
2, 3, 2, 2, 6, 11, 2, 5, 5, 9, 4, 4, 2, 7, 2, 7, 10, 6, 9, 2,
2, 5, 11, 1, 8, 8, 4, 1, 2, 14, 11, 13, 20, 3, 3, 4, 16, 2, 6,
11, 9, 11, 4, 5, 6, 19, 5, 2, 6, 1, 7, 11, 3, 9, 2, 3, 6, 20,
8, 6, 2, 11, 18, 9, 3, 7, 3, 2, 1, 8, 3, 5, 6, 2, 5, 8, 11, 4,
9, 7, 2, 12, 8, 2, 9, 5, 4, 15, 5, 13, 5, 10, 13, 7, 6, 1, 12,
12, 10, 4, 2, 16, 7, 17, 11, 18, 4, 3, 12, 1, 3, 7, 3, 6, 5,
11, 10, 12, 6, 14, 8, 6, 7, 8, 5, 10, 12, 6, 13, 3, 11, 14, 7,
9, 9, 4, 13, 4, 2, 1, 2, 2, 1, 7, 9, 3, 10, 3, 2, 1, 3, 1, 4,
2, 4, 5, 4, 2, 13, 4, 1, 3, 1, 11, 4, 1, 3, 3, 7, 5, 4, 5, 6,
1, 2, 1, 2, 1, 6, 1, 7, 6, 9, 5, 1, 6, 3, 2, 3, 3, 8, 8, 3, 2,
2, 4, 2, 5, 2, 6, 8, 11, 1, 6, 3, 3, 4, 5, 5, 7, 4, 2, 7, 3,
3, 1, 3, 9, 5, 2, 4, 12, 1, 4, 5, 2, 7, 6, 1, 2, 6, 4, 2, 7,
3, 5, 5, 3, 7, 1, 5, 2, 1, 15, 3, 5, 2, 5, 13, 6, 2, 3, 5, 2,
8, 4, 2, 6, 7, 2, 4, 1, 13, 8, 2, 1, 2, 1, 1, 5, 2, 1, 6, 11,
4, 1, 7, 7, 4, 3, 5, 1, 4, 10, 1, 2, 6, 1, 11, 3, 8, 9, 2, 6,
8, 11, 14, 16, 4, 1, 4, 2, 1, 10, 4, 9, 3, 12, 8, 11, 8, 8, 5,
1, 4, 13, 3, 8, 5, 14, 3, 5, 5, 12, 1, 3, 4, 5, 2, 7, 6, 9, 6,
10, 5, 2, 3, 2, 10, 10, 10, 10, 10, 1, 14, 3, 5, 9, 6, 2, 2,
2, 4, 4, 11, 14, 2, 2, 2, 8, 7, 2, 10, 12, 1, 6, 10, 2, 3, 5,
10, 6, 1, 8, 4, 11, 5, 4, 3, 6, 2, 4, 6, 9, 3, 9, 11, 7, 3, 15,
3, 7, 3, 5, 4, 6, 9, 13, 8, 5, 7, 8, 8, 5, 10), Type_product = c("f",
"s", "f", "f", "f", "f", "s", "c", "s", "f", "c", "f", "f", "f",
"s", "s", "f", "f", "c", "f", "s", "f", "f", "s", "f", "c", "f",
"f", "s", "f", "f", "c", "f", "c", "f", "f", "f", "f", "f", "c",
"c", "c", "f", "f", "c", "c", "f", "c", "c", "c", "c", "c", "s",
"f", "c", "c", "c", "s", "f", "c", "f", "f", "c", "c", "f", "c",
"c", "c", "f", "c", "c", "c", "c", "c", "c", "c", "f", "c", "c",
"c", "c", "f", "c", "f", "f", "s", "f", "c", "f", "f", "f", "c",
"f", "f", "f", "f", "f", "s", "c", "c", "f", "f", "c", "c", "f",
"f", "c", "c", "f", "f", "s", "f", "c", "c", "f", "f", "f", "c",
"f", "f", "f", "c", "f", "f", "f", "f", "f", "f", "c", "f", "f",
"f", "f", "c", "s", "f", "c", "f", "f", "c", "f", "f", "f", "c",
"f", "c", "c", "c", "f", "f", "f", "f", "c", "c", "c", "f", "f",
"c", "c", "f", "c", "f", "f", "c", "c", "c", "c", "f", "f", "f",
"c", "c", "c", "f", "c", "f", "c", "f", "f", "f", "c", "f", "c",
"c", "c", "c", "c", "f", "c", "c", "c", "c", "c", "c", "c", "f",
"f", "f", "c", "f", "c", "f", "f", "c", "c", "f", "f", "f", "c",
"c", "c", "f", "c", "c", "c", "c", "c", "f", "c", "f", "f", "c",
"c", "f", "c", "f", "c", "f", "c", "c", "c", "f", "c", "c", "c",
"c", "c", "c", "c", "f", "c", "c", "f", "c", "c", "f", "f", "c",
"f", "f", "s", "c", "s", "c", "f", "c", "c", "s", "c", "c", "s",
"c", "m", "c", "c", "f", "f", "f", "f", "f", "f", "s", "f", "f",
"c", "c", "f", "c", "f", "f", "f", "c", "f", "f", "f", "s", "f",
"f", "c", "f", "c", "f", "m", "c", "c", "c", "f", "s", "f", "f",
"f", "c", "s", "c", "m", "f", "c", "m", "c", "f", "c", "f", "f",
"f", "c", "m", "f", "c", "c", "f", "c", "f", "c", "c", "c", "c",
"c", "f", "f", "f", "c", "m", "f", "m", "m", "c", "c", "c", "c",
"m", "m", "c", "f", "m", "m", "m", "m", "m", "m", "m", "m", "m",
"c", "c", "f", "f", "f", "f", "c", "f", "m", "f", "f", "f", "c",
"f", "f", "f", "c", "f", "f", "c", "c", "f", "c", "f", "c", "m",
"f", "c", "f", "c", "f", "f", "f", "f", "c", "c", "f", "f", "c",
"c", "f", "f", "f", "f", "f", "f", "c", "f", "c", "c", "f", "c",
"f", "f", "f", "f", "f", "f", "f", "c", "f", "c", "f", "c", "f",
"c", "f", "c", "f", "f", "c", "c", "c", "c", "c", "f", "f", "f",
"c", "f", "c", "f", "f", "c", "c", "f", "f", "c", "f", "c", "f",
"c", "c", "c", "f", "f", "c", "f", "c", "c", "f", "c", "f", "c",
"f", "c", "f", "c", "m", "c", "c", "m", "c", "c", "f", "c", "c",
"f", "c", "c", "c", "f", "c", "c", "m", "c", "m", "m", "c", "c",
"f", "c", "c", "c", "c", "m", "c", "c", "c", "m", "m", "m", "c",
"c", "c", "c", "m", "m", "f", "m", "m", "m", "m", "m", "m", "m",
"m", "m", "m", "m", "m", "m", "m", "m"), Exhaustion_product = structure(c(1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L,
7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L,
9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 10L, 10L, 10L, 10L, 10L, 10L,
10L, 10L, 10L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L,
6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L,
7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 8L, 8L, 8L, 8L, 8L, 8L, 8L,
8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 9L, 9L, 9L, 9L, 9L, 9L,
9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 10L, 10L, 10L, 10L,
10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 7L, 7L, 7L,
7L, 7L, 7L, 7L, 7L, 7L, 7L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L,
8L, 8L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 10L, 10L, 10L,
10L, 10L, 10L, 10L, 10L, 10L, 10L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 6L, 6L, 6L, 6L, 6L,
6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 7L, 7L, 7L, 7L, 7L,
7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 8L, 8L, 8L, 8L, 8L,
8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 9L, 9L, 9L, 9L,
9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 9L, 10L, 10L, 10L,
10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L, 10L,
10L), .Label = c("(0,10]", "(10,20]", "(20,30]", "(30,40]", "(40,50]",
"(50,60]", "(60,70]", "(70,80]", "(80,90]", "(90,100]"), class = "factor"),
Type_f = c(1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0,
1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1,
1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1,
0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0,
1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0,
1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1,
1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1,
1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1,
1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0,
1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1,
1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0,
1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0,
0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0,
1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1,
0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1,
0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1,
0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0,
0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1,
1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1,
0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1,
1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1,
0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0)), .Names = c("Type_space", "Id", "Age",
"Type_product", "Exhaustion_product", "Type_f"), row.names = c(1L,
2L, 3L, 4L, 5L, 6L, 7L, 8L, 9L, 10L, 11L, 12L, 13L, 14L, 15L,
16L, 17L, 18L, 19L, 20L, 21L, 22L, 23L, 24L, 25L, 26L, 27L, 28L,
29L, 30L, 31L, 32L, 33L, 34L, 35L, 36L, 37L, 38L, 39L, 40L, 41L,
42L, 43L, 44L, 45L, 46L, 47L, 48L, 49L, 50L, 51L, 52L, 53L, 54L,
55L, 56L, 57L, 58L, 59L, 60L, 61L, 62L, 63L, 64L, 65L, 66L, 67L,
68L, 69L, 70L, 71L, 73L, 75L, 76L, 79L, 80L, 81L, 82L, 84L, 85L,
86L, 91L, 102L, 103L, 104L, 105L, 106L, 107L, 108L, 109L, 110L,
111L, 112L, 113L, 114L, 115L, 116L, 117L, 118L, 119L, 120L, 121L,
122L, 123L, 124L, 125L, 126L, 127L, 128L, 129L, 130L, 131L, 132L,
133L, 134L, 135L, 136L, 137L, 138L, 139L, 140L, 141L, 142L, 143L,
144L, 145L, 146L, 147L, 148L, 149L, 150L, 151L, 152L, 153L, 154L,
155L, 156L, 157L, 158L, 159L, 160L, 161L, 162L, 163L, 164L, 165L,
166L, 167L, 168L, 169L, 170L, 171L, 172L, 173L, 174L, 175L, 176L,
177L, 178L, 179L, 180L, 181L, 182L, 183L, 184L, 185L, 186L, 187L,
188L, 189L, 190L, 191L, 192L, 193L, 194L, 195L, 197L, 198L, 199L,
201L, 202L, 203L, 204L, 206L, 207L, 208L, 209L, 210L, 212L, 213L,
214L, 215L, 217L, 218L, 219L, 220L, 221L, 222L, 223L, 225L, 227L,
229L, 230L, 231L, 232L, 233L, 234L, 235L, 236L, 237L, 238L, 239L,
242L, 243L, 244L, 246L, 247L, 248L, 249L, 250L, 251L, 253L, 254L,
256L, 259L, 260L, 261L, 262L, 263L, 264L, 265L, 266L, 269L, 270L,
272L, 273L, 274L, 276L, 277L, 278L, 279L, 280L, 281L, 282L, 283L,
284L, 285L, 287L, 289L, 290L, 291L, 292L, 293L, 294L, 295L, 296L,
297L, 298L, 300L, 301L, 302L, 303L, 306L, 308L, 309L, 311L, 312L,
313L, 314L, 315L, 316L, 317L, 318L, 319L, 320L, 322L, 323L, 325L,
326L, 327L, 328L, 329L, 331L, 332L, 334L, 335L, 336L, 338L, 339L,
340L, 341L, 342L, 343L, 344L, 345L, 346L, 347L, 348L, 349L, 350L,
352L, 353L, 354L, 356L, 357L, 358L, 359L, 360L, 361L, 363L, 364L,
365L, 366L, 367L, 368L, 369L, 370L, 372L, 373L, 374L, 375L, 376L,
377L, 378L, 379L, 380L, 381L, 382L, 384L, 385L, 387L, 388L, 389L,
391L, 393L, 394L, 395L, 396L, 397L, 398L, 399L, 400L, 401L, 402L,
404L, 407L, 408L, 409L, 411L, 412L, 413L, 414L, 415L, 416L, 417L,
418L, 419L, 420L, 421L, 422L, 423L, 424L, 425L, 426L, 427L, 428L,
429L, 430L, 431L, 432L, 433L, 434L, 435L, 436L, 437L, 438L, 439L,
440L, 442L, 443L, 444L, 445L, 446L, 447L, 448L, 449L, 450L, 451L,
452L, 453L, 454L, 455L, 456L, 457L, 458L, 459L, 460L, 461L, 462L,
463L, 464L, 465L, 466L, 467L, 468L, 469L, 470L, 471L, 472L, 473L,
474L, 476L, 477L, 478L, 479L, 480L, 481L, 482L, 483L, 484L, 486L,
487L, 488L, 489L, 490L, 491L, 492L, 493L, 494L, 495L, 496L, 497L,
498L, 500L, 501L, 502L, 503L, 504L, 505L, 506L, 507L, 508L, 509L,
510L, 511L, 512L, 513L, 514L, 515L, 516L, 517L, 518L, 519L, 520L,
521L, 522L, 523L, 524L, 525L, 526L, 527L, 528L, 529L, 530L, 531L,
532L, 534L, 535L, 536L, 537L, 538L, 539L, 540L, 541L, 542L, 543L,
547L, 548L, 550L, 551L, 552L, 553L, 554L, 555L, 556L, 557L, 558L,
559L, 560L, 561L, 562L, 563L, 565L, 566L, 567L, 568L, 569L, 570L,
571L, 572L, 573L, 575L, 577L, 579L, 580L, 581L, 582L, 583L, 585L,
586L, 587L, 590L, 592L, 599L, 606L, 608L), class = "data.frame")
an=Anova(glm(Type_f ~ Type_space + Exhaustion_product + Age , family=binomial,data=res))
gl=glm(Type_f ~ Type_space + Exhaustion_product + Age , family=binomial,data=res)
library("emmeans")
emmp <- emmeans( gl, pairwise ~ Exhaustion_product + Age)
summary( emmp, infer=TRUE)
(1) В случае категориальной переменной результаты очевидны. Но в случае возраста, который имеет значение в GLM, какова ценность, генерируемая в emmeans?5.455426.Это значит? Как я могу интерпретировать это?
(0,10] 5.455426 0.36901411 0.2935894 Inf -0.20641061 0.94443883 1.257 0.2088
(2) Я хочу создать графическое представление взаимодействия age а также Exhaustion_product, Также это не имеет смысла.
emmip(gl, Exhaustion_product ~ Age)
Редактировать 1 Контрастный результат
$contrasts
contrast estimate SE df asymp.LCL asymp.UCL z.ratio p.value
(0,10],5.45542635658915 - (10,20],5.45542635658915 0.33231353 0.4078967 Inf -0.95814279 1.6227698 0.815 0.9984
(0,10],5.45542635658915 - (20,30],5.45542635658915 -0.53694399 0.4194460 Inf -1.86393835 0.7900504 -1.280 0.9582
(0,10],5.45542635658915 - (30,40],5.45542635658915 -0.16100309 0.4139472 Inf -1.47060101 1.1485948 -0.389 1.0000
(0,10],5.45542635658915 - (40,50],5.45542635658915 0.40113723 0.4021403 Inf -0.87110757 1.6733820 0.998 0.9925
(0,10],5.45542635658915 - (50,60],5.45542635658915 0.60576562 0.4106536 Inf -0.69341247 1.9049437 1.475 0.9022
(0,10],5.45542635658915 - (60,70],5.45542635658915 1.38800301 0.4319258 Inf 0.02152631 2.7544797 3.214 0.0430
(0,10],5.45542635658915 - (70,80],5.45542635658915 1.01677522 0.4147441 Inf -0.29534399 2.3288944 2.452 0.2952
(0,10],5.45542635658915 - (80,90],5.45542635658915 1.99085692 0.4747929 Inf 0.48876247 3.4929514 4.193 0.0011
(0,10],5.45542635658915 - (90,100],5.45542635658915 2.03923289 0.4745872 Inf 0.53778910 3.5406767 4.297 0.0007
1 ответ
Поскольку этот вопрос кажется самообучающимся, я собираюсь привести аналогичный пример, а не те же данные. Но структура та же самая, с одним фактором и одним ковариатом в качестве предикторов.
Примером является emmeans::fiber набор данных. Его переменная отклика - прочность волокна, непрерывный предиктор - диаметр, а фактор - машина, на которой он был изготовлен.
Модель:
> mod = glm(log(strength) ~ machine + diameter, data = fiber)
> summary(mod)
... (output has been abbreviated) ...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.124387 0.068374 45.695 6.74e-14
machineB 0.026025 0.023388 1.113 0.290
machineC -0.044593 0.025564 -1.744 0.109
diameter 0.023557 0.002633 8.946 2.22e-06
(Dispersion parameter for gaussian family taken to be 0.001356412)
Анализ с использованием emmeans основан на эталонной сетке, которая по умолчанию состоит из всех уровней фактора и среднего значения ковариаты:
> ref_grid(mod)
'emmGrid' object with variables:
machine = A, B, C
diameter = 24.133
Transformation: “log”
Вы можете подтвердить в R, что mean(fiber$diameter) 24,133. Я подчеркиваю, что это среднее значение диаметра, а не что-либо в модели.
> summary(.Last.value)
machine diameter prediction SE df
A 24.13333 3.692901 0.01670845 Inf
B 24.13333 3.718925 0.01718853 Inf
C 24.13333 3.648307 0.01819206 Inf
Results are given on the log (not the response) scale.
Эти итоговые значения являются прогнозами из mod в каждой комбинации machine а также diameter, Теперь посмотрим на EMM для machine
> emmeans(mod, "machine")
machine emmean SE df asymp.LCL asymp.UCL
A 3.692901 0.01670845 Inf 3.660153 3.725649
B 3.718925 0.01718853 Inf 3.685237 3.752614
C 3.648307 0.01819206 Inf 3.612652 3.683963
Results are given on the log (not the response) scale.
Confidence level used: 0.95
... мы получаем точно такие же три предсказания. Но если мы посмотрим на diameter:
> emmeans(mod, "diameter")
diameter emmean SE df asymp.LCL asymp.UCL
24.13333 3.686711 0.009509334 Inf 3.668073 3.705349
Results are averaged over the levels of: machine
Results are given on the log (not the response) scale.
Confidence level used: 0.95
... мы получаем, что EMM равно среднему из трех предсказанных значений в эталонной сетке. И обратите внимание, что в аннотациях говорится, что результаты были усреднены по machine так что стоит прочитать это.
Чтобы получить графическое представление результатов модели, мы можем сделать
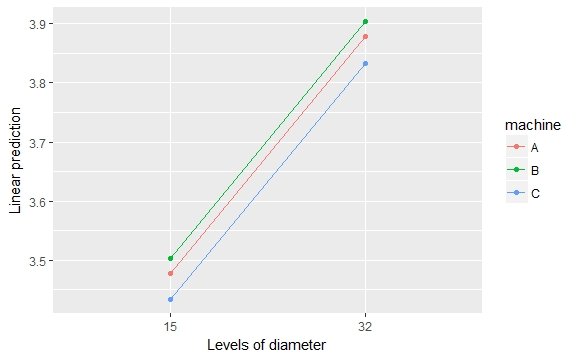
> emmip(mod, machine ~ diameter, cov.reduce = range)
Аргумент cov.reduce = range добавлен, чтобы заставить эталонную сетку использовать минимальный и максимальный диаметр, а не ее среднее значение. Без этого мы получили бы три точки вместо трех линий. На этом графике все еще показаны предсказания модели, только более детальная сетка значений. Обратите внимание, что все три линии имеют одинаковый наклон. Это потому, что модель была указана таким образом: diameter эффект добавляется к machine эффект. Таким образом, каждая линия имеет общий наклон 0,023557 (см. Вывод из summary(mod),
Для проведения теста не требуется diameter поскольку его один эффект уже проверен в summary(mod),
Одна последняя вещь. Используемая модель log(strength) как ответ. Если мы хотим, чтобы EMM были в том же масштабе, что и strength, просто добавь type = "response":
> emmeans(mod, "machine", type = "response")
machine response SE df asymp.LCL asymp.UCL
A 40.16118 0.6710311 Inf 38.86728 41.49815
B 41.22008 0.7085126 Inf 39.85455 42.63239
C 38.40960 0.6987496 Inf 37.06421 39.80384
Confidence level used: 0.95
Intervals are back-transformed from the log scale
Опять же, аннотации под результатами помогают объяснить результаты.