Сегмент дерева памяти

Question

Я видел много реализаций деревьев сегментов, которые используют O(4*N) памяти. Есть ли в любом случае для дерева сегментов использовать ровно 2*N-1 памяти? Я не могу найти реализацию, которая делает это. Даже если они говорят о сложности пространства на самом деле 2*N-1, они все равно выделяют 4*N.

РЕДАКТИРОВАТЬ: Я имею в виду, что для массива из n чисел вы используете массив из 2n-1 чисел для дерева сегментов. Каждая реализация использует массив 2*(следующая степень 2 больше, чем n).

Я знаю, что в обозначении O опущены константы, но для очень большого n будет иметь значение, если оно равно 2*N-1 или 4*N, поэтому я и задал этот вопрос.

Answer 1

O(4*N) = O(2*N) = O(N), потому что O-нотация абстрагирует постоянные факторы.

Википедия Big O обозначения

Так что вы подразумеваете под "использовать ровно 2*N-1 памяти"? Ты имеешь в виду 2*N-1 байта? Если вы имеете в виду O(2*N-1), то это то же самое, что O (4 * N), O (2 * N) и O(N).

Answer 2

Вы можете динамически добавлять узлы в дерево. Тогда узлы, которые вы не используете, просто не будут существовать и не будут тратить память.

Answer 3

Согласно обозначениям Big O, O(4*N) = O(2*N-1) = O(N). Любая стандартная реализация дерева сегментов использует линейную память.

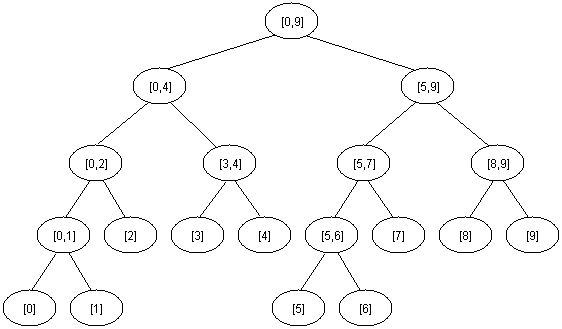
Приходя к вашему вопросу, рассмотрим массив a[0...n-1] в качестве ввода. Рассматривать n = 10, Когда вы создаете дерево сегментов, оно будет выглядеть примерно так:

Количество узлов, используемых для построения = 2*n - 1 = 19. Таким образом, теоретически, требуется только 19 узлов!

Но мы реализуем дерево сегментов, используя array структура данных. Здесь каждый узел будет соответствовать некоторому индексу в array, В сегментном дереве для индексированного узла x, левый дочерний индекс = 2*x, индекс правого ребенка = 2*x+1,

Итак, если я начну с одноиндексного массива, индекс [0, 9] = 1, [5] = 24, [6] = 25, Итак, вам нужно по крайней мере индекс до 25 в этом случае. В худшем случае вам понадобится индекс 31 в случае полностью выращенного сегмента дерева (n=16),

Таким образом, мы поддерживаем array с размером 2*(next power of 2 >= n)

Answer 4

Большинство людей знакомы с реализацией безопасной выделенной памяти 4N, которая является верхней границей для построения дерева сегментов на массиве размера N или версии ООП. Чтобы узнать об этом, прочтите здесь. Это очень хороший источник, в котором много информации упаковано в деревья сегментов.

Теперь перейдем к использованию памяти 2N. Взгляните сюда, здесь, а также:

Реализация с эффективным использованием памяти ( отсюда)

Большинство людей используют реализацию из предыдущего раздела. Если вы посмотрите на массив t, вы увидите, что он соответствует нумерации узлов дерева в порядке обхода BFS (обход уровня-порядка). При таком обходе дочерние элементы вершины v равны 2v и 2v+1 соответственно. Однако, если n не является степенью двойки, этот метод пропустит некоторые индексы и оставит некоторые части массива t неиспользованными. Потребление памяти ограничено 4n, даже несмотря на то, что для дерева сегментов массива из n элементов требуется только 2n−1 вершин. Однако его можно уменьшить. Мы меняем нумерацию вершин дерева в порядке обхода Эйлера (обхода до порядка) и записываем все эти вершины рядом друг с другом.

Давайте посмотрим на вершину с индексом v, пусть он отвечает за сегмент [l,r], и пусть mid=l+r2. Очевидно, что у левого потомка будет индекс v+1. Левый дочерний элемент отвечает за сегмент [l,mid], т.е. всего в поддереве левого дочернего элемента будет 2∗(mid−l+1)−1 вершина. Таким образом, мы можем вычислить индекс правого потомка v. Индекс будет v+2∗(mid−l+1). Этой нумерацией мы добиваемся уменьшения необходимой памяти до 2n.