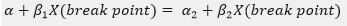Кусочно-линейная регрессия с ограничением - r

Question

Я пытаюсь сделать кусочно-линейный анализ регрессии OLS в R с одной точкой останова. У меня есть следующая формула регрессии и ограничения: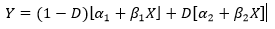

Где D - манекен Я хотел бы наложить ограничение, чтобы линии регрессии были непрерывными (с точкой разрыва). Ограничение ниже будет работать нормально.

У меня вопрос, как мне сформулировать это в lm()-функции в R? Ранее я пробовал "сегментированный" пакет, но мне нужно интерпретировать перехваты для обеих строк в сводке регрессии.

Я предоставил некоторые данные ниже. Точка останова здесь равна 0, поэтому d 1 для х>= 0 .

             x          y d
1    4.3047451 11.2660463 1
2    7.0062423 -3.2897982 1
3    2.7862009 -2.8232636 1
4   -0.8662964  0.4051925 0
5   -0.9553261 -0.9228929 0
6   -1.6626654  3.5044546 0
7    3.4906905  1.4961349 1
8   -0.7072658 -0.2758436 0
9   -7.0054069 -1.3041742 0
10  -2.2510701 -0.1848814 0
11 -13.3617905 -0.2113756 0
12   4.1001251  0.2845748 1
13  -4.6575944 -1.1603290 0
14   5.2243857  3.8324236 1
15   3.5003320 -2.3672985 1
16 -13.2623113 -7.1593177 0
17  -1.7944354 -2.1725478 0
18   0.5885924 -0.2411048 1
19 -19.3744936 -0.1982088 0
20 -17.9876978 -1.5995063 0

Редактировать:

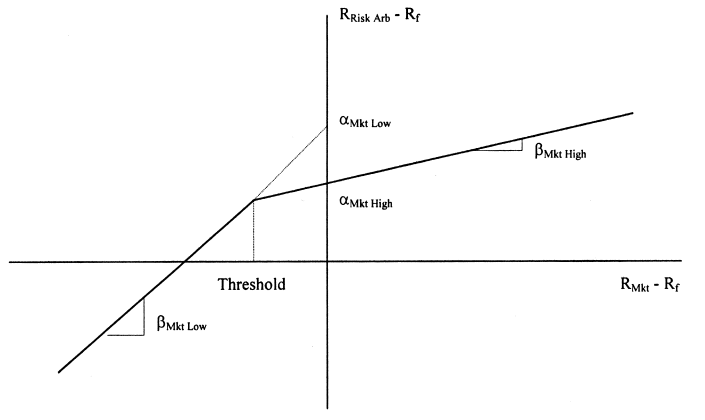
Я добавил графическое представление того, что я пытаюсь выполнить. Важно, чтобы 2 подогнанные линии встретились на пороге, и чтобы я мог получить 4 коэффициента. 2 альфы и 2 бета.

Answer 1

Так как точка останова x = 0, мы имеем a = a2 и так:

nls( y ~ (x < 0) * (a + b * x) + (x > 0) * (a + b2 * x), dat,
  start = list(a = 1, b = 1, b2 = 1))

или используя lm

lm(y ~ I(x * (x < 0)) + I(x * (x > 0)), dat)

В общем случае, если B является точкой останова:

B <- 0
nls( y ~ (x < B) * (a + b * (x - B)) + (x > B) * (a + b2 * (x - B)), dat,
  start = list(a = 1, b = 1, b2 = 1))

B <- 0
lm(y ~ I((x - B) * (x < B)) + I((x - B) * (x > B)), dat)

Answer 2

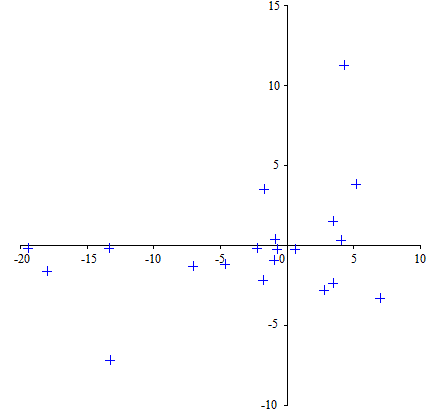
Это не ответ, а комментарий, который нельзя отредактировать в разделе комментариев, потому что он требует, чтобы изображение было понятным.

На самом деле, я не могу понять ваши данные: когда они представлены на декартовой диаграмме (ниже), точки выглядят очень разбросанными. Это не похоже на кусочную функцию. Что мне не хватает?

Кстати, если точки были не слишком далеко от кусочной функции, состоящей из двух наклонных сегментов, существует очень простой способ подгонки. См. Страницы 12-13 в этом документе: https://fr.scribd.com/document/380941024/Regression-par-morceaux-Piecewise-Regression-pdf