Преобразовать числовую модель теплопроводности Matlab в Python
Я пытаюсь преобразовать свою модель Matlab для переходной теплопроводности в Python. К сожалению, результаты моего численного решения в Python не совпадают с результатами модели Matlab. Я использую Spyder IDE для написания своего кода.
Основные различия между Matlab и Python для моей модели (которые я нашел до сих пор):
- Индексы Matlab для массивов начинаются с 1, тогда как индекс Python начинается с 0
- решение для A*x = B в Matlab
x = A \ Bтогда как в Python этоx = np.linalg.solve(A,B) - изменение вектора столбца
col = Cк вектору строкиrowв Matlab естьrow = C'тогда как в Python этоrow = C.T
Чтобы проверить модель Matlab и Python, я сравниваю A массив. Как видите, два массива не совпадают:
Matlab...
A =
1.1411 -0.1411 0 0
-0.0118 1.0470 -0.0353 0
0 -0.0157 1.0470 -0.0313
0 0 -0.0470 1.0593
Python...
A
[[ 1.14106122 -0.14106122 0. 0. ]
[-0. 1.04702041 -0.04702041 0. ]
[ 0. -0.0235102 1.04702041 -0.0235102 ]
[ 0. 0. -0.04702041 1.05681633]]
Есть кое-что, что я не правильно делаю в коде Python. Я предполагаю, что это связано с тем, как Python индексирует массивы. Но я не уверен.
Так что любые предложения о том, как построить мою модель Matlab в Python, будут высоко оценены?
Вот пример Matlab, который я пытаюсь воспроизвести в Python:
% parameters
% -------------------------------------------------------------------------
rho = 700; % density of wood, kg/m^3
d = 0.035e-2; % wood particle diameter, m
cpw = 1500; % biomass specific heat capacity, J/kg*K
kw = 0.105; % biomass thermal conductivity, W/m*K
h = 375; % heat transfer coefficient, W/m^2*K
Ti = 300; % initial particle temp, K
Tinf = 773; % ambient temp, K
% numerical model where b = 1 cylinder and b = 2 sphere
% -------------------------------------------------------------------------
nt = 1000; % number of time steps
tmax = 0.8; % max time, s
dt = tmax/nt; % time step, s
t = 0:dt:tmax; % time vector, s
nr = 3; % number or radius steps
%nr = 100; % number or radius steps
r = d/2; % radius of particle, m
dr = r/nr; % radius step, delta r
m = nr+1; % nodes from center to surface
b = 2 ; % run model as a cylinder (b = 1) or as a sphere (b = 2)
if b == 1
shape = 'Cylinder';
elseif b == 2
shape = 'Sphere';
end
alpha = kw/(rho*cpw); % thermal diffusivity, alfa = kw / rho*cp, m^2/s
Fo = alpha*dt/(dr^2); % Fourier number, Fo = alfa*dt / dr^2, (-)
Bi = h*dr/kw; % Biot numbmer, Bi = h*dr / kw, (-)
% creat array [TT] to store temperature values, row = time step, column = node
TT = zeros(1,m);
i = 1:m;
TT(1,i) = Ti; % first row is initial temperature of the cylinder or sphere
% build coefficient matrix [A] and initial column vector {C}
A = zeros(m); % pre-allocate [A] array
C = zeros(m,1); % pre-allocate {C} vector
A(1,1) = 1 + 2*(1+b)*Fo;
A(1,2) = -2*(1+b)*Fo;
C(1,1) = Ti;
for i = 2:m-1
A(i,i-1) = -Fo*(1 - b/(2*i)); % Tm-1
A(i,i) = 1 + 2*Fo; % Tm
A(i,i+1) = -Fo*(1 + b/(2*i)); % Tm+1
C(i,1) = Ti;
end
A(m,m-1) = -2*Fo;
A(m,m) = 1 + 2*Fo*(1 + Bi + (b/(2*m))*Bi);
C(m) = Ti + 2*Fo*Bi*(1 + b/(2*m))*Tinf;
% display [A] array and [C] column vector in console
A
C
% solve system of equations [A]{T} = {C} for column vector {T}
for i = 2:nt+1
T = A\C;
C = T;
C(m) = T(m) + 2*Fo*Bi*(1 + b/(2*m))*Tinf;
TT(i,:) = T'; % store new temperatures in array [TT]
end
% plot
% -------------------------------------------------------------------------
figure(b)
plot(t,TT(:,1),'--k',t,TT(:,m),'-k')
hold on
plot([0 tmax],[Tinf Tinf],':k')
hold off
axis([0 tmax Ti-20 Tinf+20])
ylabel('Temperature (K)')
xlabel('Time (s)')
nr = num2str(nr); nt = num2str(nt); dt = num2str(dt); h = num2str(h); Tinf = num2str(Tinf);
legend('center','surface',['T\infty = ',Tinf,'K'],'location','southeast')
title([num2str(shape),', nr = ',nr,', nt = ',nt,', \Deltat = ',dt,', h = ',h])
И вот моя попытка в Python:
# use Python 3 print function
from __future__ import print_function
# libraries and packages
import numpy as np
import matplotlib.pyplot as py
# parameters
# -------------------------------------------------------------------------
rho = 700 # density of wood, kg/m^3
d = 0.035e-2 # wood particle diameter, m
cpw = 1500 # biomass specific heat capacity, J/kg*K
kw = 0.105 # biomass thermal conductivity, W/m*K
h = 375 # heat transfer coefficient, W/m^2*K
Ti = 300 # initial particle temp, K
Tinf = 773 # ambient temp, K
# numerical model where b = 1 cylinder and b = 2 sphere
# -------------------------------------------------------------------------
nt = 1000 # number of time steps
tmax = 0.8 # max time, s
dt = tmax/nt # time step, s
t = np.arange(0,tmax+dt,dt)
nr = 3 # number or radius steps
r = d/2 # radius of particle, m
dr = r/nr # radius step, delta r
m = nr+1 # nodes from center m=0 to surface m=steps+1
b = 2 # run model as a cylinder (b = 1) or as a sphere (b = 2)
alpha = kw/(rho*cpw) # thermal diffusivity, alfa = kw / rho*cp, m^2/s
Fo = alpha*dt/(dr**2) # Fourier number, Fo = alfa*dt / dr^2, (-)
Bi = h*dr/kw # Biot numbmer, Bi = h*dr / kw, (-)
# create array [TT] to store temperature values, row = time step, column = node
TT = np.zeros((1,m))
# first row is initial temperature of the cylinder or sphere
for i in range(0,m):
TT[0,i] = Ti
# build coefficient matrix [A] and initial column vector {C}
A = np.zeros((m,m)) # pre-allocate [A] array
C = np.zeros((m,1)) # pre-allocate {C} vector
A[0, 0] = 1 + 2*(1+b)*Fo
A[0, 1] = -2*(1+b)*Fo
C[0, 0] = Ti
for i in range(1, m-1):
A[i, i-1] = -Fo*(1 - b/(2*i)) # Tm-1
A[i, i] = 1 + 2*Fo # Tm
A[i, i+1] = -Fo*(1 + b/(2*i)) # Tm+1
C[i, 0] = Ti
A[m-1, m-2] = -2*Fo
A[m-1, m-1] = 1 + 2*Fo*(1 + Bi + (b/(2*(m-1)))*Bi)
C[m-1, 0] = Ti + 2*Fo*Bi*(1 + b/(2*(m-1)))*Tinf
# print [A] and [C] to console
print('A \n', A)
print('C \n', C)
# solve system of equations [A]{T} = {C} for column vector {T}
for i in range(1, nt+1):
T = np.linalg.solve(A,C)
C = T
C[m-1, 0] = T[m-1, 0] + 2*Fo*Bi*(1 + b/(2*(m-1)))*Tinf
TT = np.vstack((TT, T.T))
# plot results
py.figure(1)
py.plot(t,TT[:, m-1])
py.plot(t,TT[:, 0])
py.grid()
py.show()
Что касается сгенерированного графика Python (см. Изображение ниже), сплошные (красные и черные) линии и пунктирные (красные и черные) линии должны располагаться друг над другом. Выполнение приведенного выше кода в nr = 99 сплошная линия Python не соответствует сплошной красной линии Matlab, но пунктирные линии графиков Python и Matlab действительно совпадают. Это говорит мне, что что-то не так в последнем for цикл кода Python. Может быть, способ, которым я решаю A*x = B в Python, не верен?
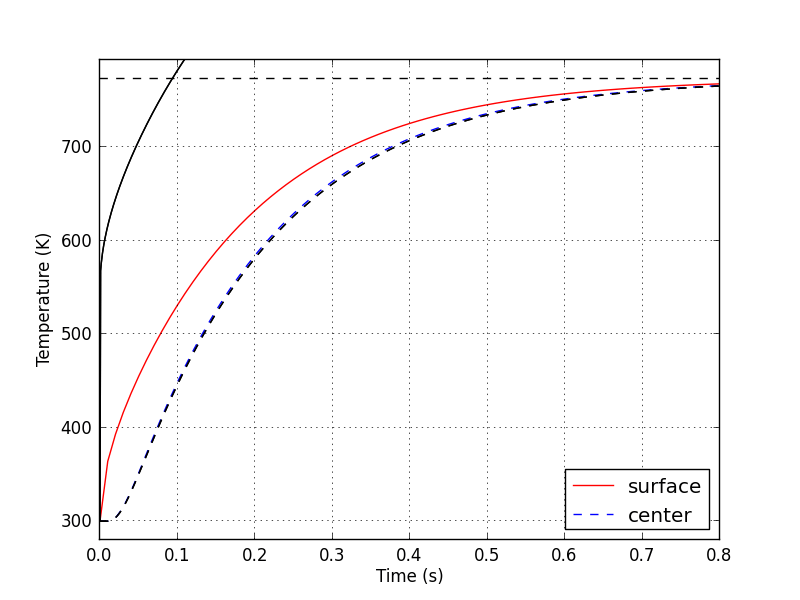
1 ответ
Значение индекса в цикле, который генерирует A изменился на 1, поэтому эти две строки
A[i, i-1] = -Fo*(1 - b/(2*i)) # Tm-1
A[i, i+1] = -Fo*(1 + b/(2*i)) # Tm+1
должно быть
A[i, i-1] = -Fo*(1 - b/(2*(i+1))) # Tm-1
A[i, i+1] = -Fo*(1 + b/(2*(i+1))) # Tm+1
Обратите внимание на изменение от i в i+1 в формулах (но не в индексировании A).
С другой стороны, значение m не изменился, поэтому вы не должны были изменить m в m-1 в формулах, которые вычисляют края A а такжеC, То есть измените эти строки:
A[m-1, m-1] = 1 + 2*Fo*(1 + Bi + (b/(2*(m-1)))*Bi)
C[m-1, 0] = Ti + 2*Fo*Bi*(1 + b/(2*(m-1)))*Tinf
...
C[m-1, 0] = T[m-1, 0] + 2*Fo*Bi*(1 + b/(2*(m-1)))*Tinf
в
A[m-1, m-1] = 1 + 2*Fo*(1 + Bi + (b/(2*m))*Bi)
C[m-1, 0] = Ti + 2*Fo*Bi*(1 + b/(2*m))*Tinf
...
C[m-1, 0] = T[m-1, 0] + 2*Fo*Bi*(1 + b/(2*m))*Tinf
Кроме того, как указал острый глаз @eryksun в комментарии, C = T должно быть C = T.copy(), В Matlab память управляется с помощью "копирования при записи", поэтому изменение на месте C после этого назначения не влияет T, С няшкой, C = T марки C а также T ссылки на один и тот же базовый объект массива; изменения C на месте также меняется T, Чтобы воссоздать поведение Matlab, C должна быть копия T,