Алгоритм нахождения точки пересечения двух линейных отрезков 3D

Question

Алгоритм нахождения точки пересечения двух линейных отрезков 3D

Найти точку пересечения для двух отрезков линии 2D легко; Формула проста. Но нахождение точки пересечения для двух отрезков 3D линии, я не боюсь.

Какой алгоритм в C# предпочтительно находит точку пересечения двух трехмерных отрезков?

Я нашел реализацию C++ здесь. Но я не доверяю решению, потому что оно отдает предпочтение определенной плоскости (посмотрите на способ perp реализуется в разделе реализации, он предполагает предпочтение z plane, Любой общий алгоритм не должен предполагать какую-либо плоскую ориентацию или предпочтение).

Есть ли лучшее решение?

28

c# math

Источник

user3834 23 фев '10 в 07:49

10 ответов

Решение

Большинство 3D линий не пересекаются. Надежный метод - найти самую короткую линию между двумя 3D линиями. Если самая короткая линия имеет нулевую длину (или расстояние меньше любого указанного вами допуска), то вы знаете, что две исходные линии пересекаются.

Метод нахождения самой короткой линии между двумя трехмерными линиями, написанный Полом Бурком, резюмируется / перефразируется следующим образом:

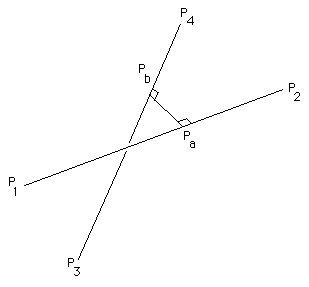
В дальнейшем линия будет определяться двумя лежащими на ней точками, а точка на линии "а", определяемая точками P1 и P2, имеет уравнение
Pa = P1 + mua (P2 - P1)
аналогично точка во второй строке "b", определяемая точками P4 и P4, будет записана как
Pb = P3 + mub (P4 - P3)
Значения mua и mub варьируются от отрицательной до положительной бесконечности. Сегменты линии между P1 P2 и P3 P4 имеют свои соответствующие mu между 0 и 1.
Существует два подхода к поиску самого короткого отрезка между линиями "а" и "б".

Подход один:

Первый - записать длину отрезка, соединяющего две линии, а затем найти минимум. То есть минимизировать следующее
|| Pb - Pa ||^2
Подстановка уравнений линий дает
|| P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ||^2
Вышеизложенное можно затем развернуть в (x,y,z) компонентах.
Есть условия, которые должны быть выполнены как минимум, производная по mua и mub должна быть равна нулю.... вышеупомянутая функция имеет только один минимум и никаких других минимумов или максимумов. Эти два уравнения могут быть затем решены для mua и mub, фактических точек пересечения, найденных путем подстановки значений mu в исходные уравнения линии.

Подход второй:

Альтернативный подход, который дает точно такие же уравнения, состоит в том, чтобы понять, что самый короткий отрезок линии между двумя линиями будет перпендикулярен двум линиям. Это позволяет нам написать два уравнения для скалярного произведения в виде
(Pa - Pb) dot (P2 - P1) = 0
(Pa - Pb) dot (P4 - P3) = 0
Расширяя их, учитывая уравнение линий
( P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ) dot (P2 - P1) = 0
( P1 - P3 + mua (P2 - P1) - mub (P4 - P3) ) dot (P4 - P3) = 0
Расширяя их в терминах координат (x,y,z) ... результат следующий
d1321 + mua d2121 - mub d4321 = 0
d1343 + mua d4321 - mub d4343 = 0
где
dmnop = (xm - xn)(xo - xp) + (ym - yn)(yo - yp) + (zm - zn)(zo - zp)
Обратите внимание, что dmnop = dopmn
Наконец, решение для муа дает
mua = ( d1343 d4321 - d1321 d4343 ) / ( d2121 d4343 - d4321 d4321 )
и обратно заменив дает муб
mub = ( d1343 + mua d4321 ) / d4343

Этот метод был найден на сайте Пола Бурка, который является отличным ресурсом по геометрии. Сайт был реорганизован, поэтому прокрутите вниз, чтобы найти тему.

27

Источник

user123346 23 фев '10 в 09:18

// This code in C++ works for me in 2d and 3d

// assume Coord has members x(), y() and z() and supports arithmetic operations
// that is Coord u + Coord v = u.x() + v.x(), u.y() + v.y(), u.z() + v.z()

inline Point
dot(const Coord& u, const Coord& v) 
{
return u.x() * v.x() + u.y() * v.y() + u.z() * v.z();   
}

inline Point
norm2( const Coord& v )
{
return v.x() * v.x() + v.y() * v.y() + v.z() * v.z();
}

inline Point
norm( const Coord& v ) 
{
return sqrt(norm2(v));
}

inline
Coord
cross( const Coord& b, const Coord& c) // cross product
{
return Coord(b.y() * c.z() - c.y() * b.z(), b.z() * c.x() - c.z() * b.x(), b.x() *  c.y() - c.x() * b.y());
}

bool 
intersection(const Line& a, const Line& b, Coord& ip)
// http://mathworld.wolfram.com/Line-LineIntersection.html
// in 3d; will also work in 2d if z components are 0
{
Coord da = a.second - a.first; 
Coord db = b.second - b.first;
    Coord dc = b.first - a.first;

if (dot(dc, cross(da,db)) != 0.0) // lines are not coplanar
    return false;

Point s = dot(cross(dc,db),cross(da,db)) / norm2(cross(da,db));
if (s >= 0.0 && s <= 1.0)
{
    ip = a.first + da * Coord(s,s,s);
    return true;
}

return false;
}

6

Источник

user1334366 23 апр '12 в 21:39

Я попытался ответить @Bill, и на самом деле он не работает каждый раз, что я могу объяснить. На основании ссылки в его коде. Давайте, например, эти два отрезка линии AB и CD.

A = (2,1,5), B = (1,2,5) и C=(2,1,3) и D=(2,1,2)

когда вы пытаетесь получить перекресток, он может сказать вам, что это точка А (неверная) или пересечения нет (правильная). В зависимости от порядка размещения этих сегментов.

х = А +(БА) с
х = С +(постоянный ток) т

Билл решил за s, но так и не решил t. А поскольку вы хотите, чтобы эта точка пересечения находилась на обоих отрезках, s и t должны быть из интервала <0,1>. То, что на самом деле происходит в моем примере, это то, что только s, если из этого интервала и т равен -2. A лежит на линии, определенной C и D, но не на линейном сегменте CD.

var s = Vector3.Dot(Vector3.Cross(dc, db), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

var t = Vector3.Dot(Vector3.Cross(dc, da), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

где da - BA, db - DC, а dc -CA, я просто сохранил имена, предоставленные Биллом.

Тогда, как я уже сказал, вы должны проверить, что и s, и t имеют значение <0,1>, и вы можете вычислить результат. На основе формулы выше.

if ((s >= 0 && s <= 1) && (k >= 0 && k <= 1))
{
   Vector3 res = new Vector3(this.A.x + da.x * s, this.A.y + da.y * s, this.A.z + da.z * s);
}

Еще одна проблема с ответом Билла состоит в том, когда две линии коллинеарны и имеется более одной точки пересечения. Там будет деление на ноль. Вы хотите избежать этого.

6

Источник

user1456174 20 ноя '15 в 11:44

Первоисточник, который вы упомянули, предназначен только для 2-го случая. Реализация для perp в порядке. Использование x и y - это просто переменные, а не показатель предпочтения конкретной плоскости.

На том же сайте есть это для трехмерного случая: " http://geomalgorithms.com/a07-_distance.html"

Похоже, Эберли написал ответ: " https://www.geometrictools.com/Documentation/DistanceLine3Line3.pdf"

Помещаю это здесь, потому что Google указывает на геомалгоритмы и на этот пост.

2

Источник

user1633759 10 апр '19 в 20:21

Но нахождение точки пересечения для двух отрезков 3D линии, я не боюсь.

Я думаю, что это. Вы можете найти точку пересечения точно так же, как в 2d (или любом другом измерении). Единственное отличие состоит в том, что результирующая система линейных уравнений, скорее всего, не будет иметь решения (то есть линии не пересекаются).

Вы можете решить общие уравнения вручную и просто использовать свое решение или решить его программно, используя, например, гауссовское вычисление.

1

Источник

user276070 23 фев '10 в 08:34

Я нашел ответ!

в ответе сверху я нашел эти уравнения:

Уравнение №1: var s = Vector3.Dot(Vector3.Cross(dc, db), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

Уравнение № 2: var t = Vector3.Dot(Vector3.Cross(dc, da), Vector3.Cross(da, db)) / Norm2(Vector3.Cross(da, db));

Затем я изменил #3-е уравнение:

Уравнение № 3:

if ((s >= 0 && s <= 1) && (k >= 0 && k <= 1))
{
   Vector3 res = new Vector3(this.A.x + da.x * s, this.A.y + da.y * s, this.A.z + da.z * s);
}

И, сохранив одинаковое уравнение №1 и уравнение №2, я создал следующие уравнения:

MyEq#1: Vector3f p0 = da.mul(s).add(A<vector>);MyEq#2: Vector3f p1 = db.mul(t).add(C<vector>);

Затем я решил создать еще три уравнения:

MyEq#3: Vector3f p0z = projUV(da, p0).add(A<vector>);MyEq#4: Vector3f p1z = projUV(db, p1).add(C<vector>);

и, наконец, чтобы получить вычитание двух величин projUV(1, 2), вы получите предел погрешности от 0 до 0,001f, чтобы определить, пересекаются ли две линии.

MyEq#5: var m = p0z.magnitude() - p1z.magnitude();

Напоминаю, что это было сделано на Java. Это объяснение не готово к соглашению Java. Просто используйте приведенные выше уравнения. (Совет: пока не трансформируйтесь в Мировое пространство, чтобы обе проекции УФ-уравнений попадали именно туда, куда вы хотите).

И эти уравнения визуально верны в моей программе.

0

Источник

user11345631 08 янв '20 в 09:06

Я бы начал с рассмотрения соответствующей проблемы пересечения линий. Допустим, первая линия проходит через точку p1 и параллельна вектору v1, а вторая линия проходит через точку p2 и параллельна вектору v2. Как некоторые уже заметили, в 3D две линии редко пересекаются. Но если предположить, что да, то точку пересечения q можно записать как

q = p2 + t * v2

где

t = точка(p1 - p2, v3) / точка(v2, v3)

и где

v3 = крест(перекрест(v1, v2), v1).

Поскольку мы предполагаем, что две линии пересекаются, они лежат в одной плоскости. Вектор, найденный путем векторного произведения v1 и v2, ортогонален этой плоскости. Взятие следующего векторного произведения с v1 помещает v3 обратно в плоскость, но также ортогонально v1. Тогда трехмерную задачу можно рассматривать как двумерную, что приводит к выражению для t.

Имея решение проблемы пересечения прямых, проблема пересечения сегментов теперь сводится просто к проверке того, лежит ли q на обоих сегментах. Чтобы определить, лежит ли q в первом сегменте, достаточно просто сравнить скалярные произведения. Второй сегмент проверить еще проще, поскольку приведенное выше выражение для q всегда помещает q на вторую строку, т. е. нам просто нужно проверить значение t.

0

Источник

user10661516 03 окт '23 в 23:52

Я попытался прокомментировать ответ Билла от 23 апреля 2012 г., но на сайте мне сказали, что у меня недостаточно репутации для комментариев. Тем не менее, при тестировании я обнаружил, что написанная функция correction() решает половину исходной проблемы, которая заключалась в алгоритме нахождения точки пересечения двух отрезков 3D-линии .

Если предположить, что линии компланарны, есть 5 возможных вариантов ответа на этот вопрос:

Отрезки параллельны, поэтому не пересекаются, или
Сегменты линии не параллельны, и линии бесконечной длины, на которых они лежат, действительно пересекаются, но точка пересечения не находится в границах ни сегмента линии, ни,
Линии пересекаются, и точка пересечения находится в пределах линии a, но не линии b, или,
Линии пересекаются, и точка пересечения находится в пределах линии b, но не линии a, или,
Линии пересекаются, и точка пересечения находится в пределах границ обоих сегментов линии.

Функция Боба crossction () возвращает true, когда линии пересекаются, и точка пересечения находится в пределах линии a, но возвращает false, если линии пересекаются, а точка пересечения находится в пределах только линии b.

Но если вы дважды вызываете correct (), сначала с линиями a, затем b, а затем второй раз с линиями b и a (первый и второй параметры поменяны местами), тогда, если оба вызова возвращают true, то пересечение содержится в обоих сегментах линии ( случай 5). Если оба вызова возвращают false, то ни один из сегментов линии не содержит пересечения (случай 2). Если только один из вызовов возвращает истину, то сегмент, переданный в качестве первого параметра этого вызова, содержит точку пересечения (случаи 3 или 4).

Кроме того, если возврат от вызова к norm2(cross(da,db)) равен 0,0, то отрезки линии параллельны (случай 1).

Еще одна вещь, которую я заметил при тестировании, заключается в том, что с числами с плавающей запятой фиксированной точности, которые часто используются в коде, для точки (dc, cross(da,db)) может быть довольно необычно возвращать 0,0, поэтому возвращается false, когда ее не случай может быть не то, что вы хотите. Возможно, вы захотите ввести порог, ниже которого код продолжит выполнение, а не вернет false. Это указывает на то, что сегменты линии наклонены в 3D, но в зависимости от вашего приложения вы можете допустить небольшой перекос.

Последнее, что я заметил, - это утверждение в коде Билла:

ip = a.first + da * Coord(s,s,s);

Этот da * Coord(s,s,s) выглядит как умножение вектора на вектор. Когда я заменил его скалярным числом, кратным да * с, я обнаружил, что он работает нормально.

Но в любом случае большое спасибо Бобу. Он понял сложную часть.

0

Источник

19 июн '21 в 00:44

https://bloodstrawberry.tistory.com/1037 Этот блог был реализован Unity c#.

      Vector3 getContactPoint(Vector3 normal, Vector3 planeDot, Vector3 A, Vector3 B)
{
    Vector3 nAB = (B - A).normalized;

    return A + nAB * Vector3.Dot(normal, planeDot - A) / Vector3.Dot(normal, nAB);
}

(Vector3 point1, Vector3 point2) getShortestPath(Vector3 A, Vector3 B, Vector3 C, Vector3 D)
{
    Vector3 AB = A - B;
    Vector3 CD = C - D;
    Vector3 line = Vector3.Cross(AB, CD);
    Vector3 crossLineAB = Vector3.Cross(line, AB);
    Vector3 crossLineCD = Vector3.Cross(line, CD);

    return (getContactPoint(crossLineAB, A, C, D), getContactPoint(crossLineCD, C, A, B));
}

0

Источник

JH KIM 25 ноя '22 в 18:48

Другие вопросы по тегам c# math

user3834 23 фев '10 в 09:16 2010-02-23 09:16 · Accepted Answer · 2010-02-23 09:16

Я нашел решение: это здесь.

Идея состоит в том, чтобы использовать векторную алгебру, использовать dot а также cross просто вопрос до этой стадии:

a (V1 X V2) = (P2 - P1) X V2

и рассчитать a,

Обратите внимание, что эта реализация не должна иметь какие-либо плоскости или оси в качестве ссылки.