Могу ли я извлечь периодические компоненты, используя вторые наименьшие собственные значения ошибки периодичности?
Я хочу обнаружить периодические компоненты в каналах ЭЭГ, используя Анализ периодических компонентов. Я кратко опишу процедуру, потому что алгоритм не очень хорошо известен.
Я минимизирую периодичность ошибки функции: error(τ)= E[s(t+τ) -s(t)] / E[s(t)^2], где τ это временная задержка. Если я определю матрицы A(τ), C, error(τ)=(w'*A(τ)*w)/(w'*C*w) = Rayleigh(A(τ), C, w), Таким образом, его минимальное значение является наименьшим обобщенным собственным значением (Α(τ), C), на определенный промежуток времени τ.
я бегу piCA для диапазона временных задержек и обычно я обнаруживаю периоды периодических компонентов в локальных минимумах функции минимизированной ошибки (используя наименьшие обобщенные собственные значения). [E,W]=piCA( Xeeg, [minlag maxlag], 'pre', [1 1 1]);которая дает матрицу преобразования W и матрица E обобщенных собственных значений всех пар (A[τ],C).
Можно ли определить правильные периодические компоненты при локальных минимумах НЕ функции, рассчитанной с наименьшими собственными значениями, НО со вторыми наименьшими собственными значениями??
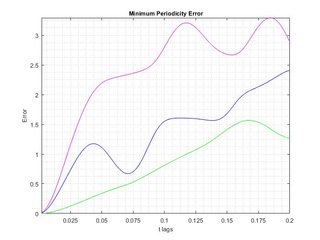
Смотрите изображение ниже:
Зеленая линия, очевидно, является функцией минимальной ошибки для всех временных лагов, но она не имеет локальных минимумов!!! Таким образом, результаты могут быть получены только из функции синей линии, которая рассчитывается с использованием вторых наименьших собственных значений.:/