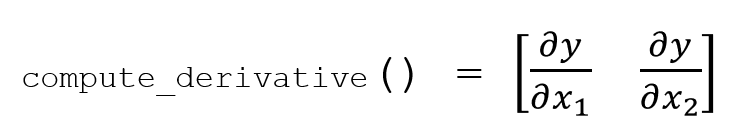Вычисление частных производных глубокой нейронной сети относительно входов
Я пытаюсь вычислить производную нейронной сети с 2 или более скрытыми слоями относительно ее входных данных. Так что не "стандартное обратное распространение", так как меня не интересует, как выходные данные меняются по отношению к весам. И я не собираюсь обучать свою сеть, используя ее (если это требует удаления тега обратного распространения, дайте мне знать, но я подозреваю, что то, что мне нужно, не слишком отличается)
Причина моего интереса к производной здесь заключается в том, что у меня есть тестовый набор, который иногда предоставляет мне соответствующий [x1, x2] : [y] пара, а иногда [x1, x2] : [d(y)/dx1] или же [x1, x2] : [d(y)/dx2], Затем я использую алгоритм роя частиц для обучения своей сети.
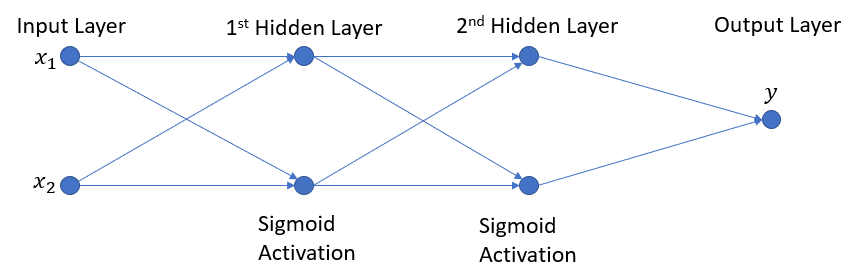
Мне нравятся диаграммы, поэтому, чтобы сохранить несколько слов, вот моя сеть:
и что я хотел бы для compute_derivativeметод для возврата массива numpy формы ниже:
Пока это моя попытка, но я не могу получить массив, соответствующий моему количеству входов в конце. Я не могу понять, что я делаю неправильно.
def compute_derivative(self):
"""Computes the network derivative and returns an array with the change in output with respect to each input"""
self.compute_layer_derivative(0)
for l in np.arange(1,self.size):
dl = self.compute_layer_derivative(l)
dprev = self.layers[l-1].derivatives
self.output_derivatives = dl.T.dot(dprev)
return self.output_derivatives
def compute_layer_derivative(self, l_id):
wL = self.layers[l_id].w
zL = self.layers[l_id].output
daL = self.layers[l_id].f(zL, div=1)
daLM = np.repeat(daL,wL.shape[0], axis=0)
self.layers[l_id].derivatives = np.multiply(daLM,wL)
return self.layers[l_id].derivatives
Если вы хотите запустить весь код, я сделал урезанную, закомментированную версию, которая будет работать с копировальной пастой (см. Ниже). Спасибо за помощь!
# -*- coding: utf-8 -*-
import numpy as np
def sigmoid(x, div = 0):
if div == 1: #first derivative f'
return np.exp(-x) / (1. + np.exp(-x))**2.
if div == 2: # second derivative f''
return - np.exp(x) * (np.exp(x) - 1) / (1. + np.exp(x))**3.
return 1. / (1. + np.exp(-x)) # f
def linear(x, div = 0):
if div == 1: #first derivative f'
return np.full(x.shape,1)
if div > 2: # second derivative f''
return np.zeros(x.shape)
return x # f
class Layer():
def __init__(self, in_n, h_n, activation, bias = True, debug = False):
self.w = 2*np.random.random((in_n, h_n)) - 1 # synaptic weights with 0 mean
self.f = activation
self.output = None
self.activation = None
self.derivatives = np.array([[None for i in range(in_n+1)]]) #+1 for global dev
if bias:
self.b = 2*np.random.random((1, h_n)) - 1
else:
self.b = None
if debug:
self.w = np.full((in_n, h_n), 1.)
if self.b is not None: self.b = np.full((1, h_n), 1.)
def compute(self, inputs):
if self.w.shape[0] != inputs.shape[1]:
raise ValueError("Inputs dimensions do not match test data dim.")
if self.b is None:
self.output = np.dot(inputs, self.w)
else:
self.output = np.dot(inputs, self.w) + self.b
self.activation = self.f(self.output)
class NeuralNetwork():
def __init__(self, nb_layers, in_NN, h_density, out_NN, debug = False):
self.debug = debug
self.layers = []
self.size = nb_layers+1
self.output_derivatives = None
self.output = None
self.in_N = in_NN
self.out_N = out_NN
if debug:
print("Input Layer with {} inputs.".format(in_NN))
#create hidden layers
current_inputs = in_NN
for l in range(self.size - 1):
self.layers.append(Layer(current_inputs, h_density, sigmoid, debug = debug))
current_inputs = h_density
if debug:
print("Hidden Layer {} with {} inputs and {} neurons.".format(l+1, self.layers[l].w.shape[0], self.layers[l].w.shape[1]))
#creat output layer
self.layers.append(Layer(current_inputs, out_NN, linear, bias=False, debug = debug))
if debug:
print("Output Layer with {} inputs and {} outputs.".format(self.layers[-1].w.shape[0], self.layers[-1].w.shape[1]))
#print("with w: {}".format(self.layers[l].w))
print("ANN size = {}, with {} Layers\n\n".format( self.size, len(self.layers)))
def compute(self, point):
curr_inputs = point
for l in range(self.size):
self.layers[l].compute(curr_inputs)
curr_inputs = self.layers[l].activation
self.output = curr_inputs
if self.debug: print("ANN output: ",curr_inputs)
return self.output
def compute_derivative(self, order, point):
""" If the network has not been computed, compute it before getting
the derivative. This might be a bit expensive..."""
if self.layers[self.size-1].output is None:
self.compute(point)
#Compute output layer total derivative
self.compute_layer_derivative(self.size-1, order)
self.output_derivatives = self.get_partial_derivatives_to_outputs(self.size-1)
print(self.output_derivatives)
for l in np.arange(1,self.size):
l = self.size-1 - l
self.compute_layer_derivative(l, order)
if l > 0: #if we are not at first hidden layer compute the total derivative
self.output_derivatives *= self.get_total_derivative_to_inputs(l)
else:# get the each output derivative with respect to each input
backprop_dev_to_outs = np.repeat(np.matrix(self.output_derivatives),self.in_N, axis=0).T
dev_to_inputs = np.repeat(np.matrix(self.get_partial_derivatives_to_inputs(l)).T,self.out_N, axis=1).T
self.output_derivatives = np.multiply(backprop_dev_to_outs, dev_to_inputs)
if self.debug: print("output derivatives: ",self.output_derivatives)
return self.output_derivatives
def get_total_derivative(self,l_id):
return np.sum(self.get_partial_derivatives_to_inputs(l_id))
def get_total_derivative_to_inputs(self,l_id):
return np.sum(self.get_partial_derivatives_to_inputs(l_id))
def get_partial_derivatives_to_inputs(self,l_id):
return np.sum(self.layers[l_id].derivatives, axis=1)
def get_partial_derivatives_to_outputs(self,l_id):
return np.sum(self.layers[l_id].derivatives, axis=0)
def compute_layer_derivative(self, l_id, order):
if self.debug: print("\n\ncurrent layer is ", l_id)
wL = self.layers[l_id].w
zL = self.layers[l_id].output
daL = self.layers[l_id].f(zL, order)
daLM = np.repeat(daL,wL.shape[0], axis=0)
self.layers[l_id].derivatives = np.multiply(daLM,wL)
if self.debug:
print("L_id: {}, a_f: {}".format(l_id, self.layers[l_id].f))
print("L_id: {}, dev: {}".format(l_id, self.get_total_derivative_to_inputs(l_id)))
return self.layers[l_id].derivatives
#nb_layers, in_NN, h_density, out_NN, debug = False
nn = NeuralNetwork(1,2,2,1, debug= True)
nn.compute(np.array([[1,1]]))# head value
nn.compute_derivative(1,np.array([[1,1]])) #first derivative
РЕДАКТИРОВАННЫЙ ОТВЕТ НА ОСНОВЕ ОТВЕТА СИРГУИ:
# Here we assume that the layer has sigmoid activation
def Jacobian(x = np.array([[1,1]]), w = np.array([[1,1],[1,1]]), b = np.array([[1,1]])):
return sigmoid_d(x.dot(w) + b) * w # J(S, x)
В случае сети с 2 скрытыми слоями с сигмовидной активацией и одним выходным слоем с сигмовидной активацией (так что мы можем просто использовать ту же функцию, что и выше), мы имеем:
J_L1 = Jacobian(x = np.array([[1,1]])) # where [1,1] are the inputs of to the network (i.e. values of the neuron in the input layer)
J_L2 = Jacobian(x = np.array([[3,3]])) # where [3,3] are the neuron values of layer 1 before activation
# in the output layer the weights and biases are adjusted as there is 1 neuron rather than 2
J_Lout = Jacobian(x = np.array([[2.90514825, 2.90514825]]), w = np.array([[1],[1]]), b = np.array([[1]]))# where [2.905,2.905] are the neuron values of layer 2 before activation
J_out_to_in = J_Lout.T.dot(J_L2).dot(J_L1)
1 ответ
Вот как я получил то, что должен дать ваш пример:
# i'th component of vector-valued function S(x) (sigmoid-weighted layer)
S_i(x) = 1 / 1 + exp(-w_i . x + b_i) # . for matrix multiplication here
# i'th component of vector-valued function L(x) (linear-weighted layer)
L_i(x) = w_i . x # different weights than S.
# as it happens our L(x) output 1 value, so is in fact a scalar function
F(x) = L(S(x)) # final output value
#derivative of F, denoted as J(F, x) to mean the Jacobian of the function F, evaluated at x.
J(F, x) = J(L(S(x)), x) = J(L, S(x)) . J(S, x) # chain rule for multivariable, vector-valued functions
#First, what's the derivative of L?
J(L, S(x)) = L
Обычно это удивительный результат, но вы можете проверить это самостоятельно, вычислив частные производные M . x для некоторой случайной матрицы M, Если вы вычислите все производные и поместите их в якобиан, вы вернетесь M,
#Now what's the derivative of S? Compute via formula
d(S_i(x)/dx_j) = w_ij * exp(-w_i.x+b_i) / (1 + exp(-w_i.x+b_i))**2 #w_ij, is the j'th component of the vector w_i
#For the gradient of a S_i (which is just one component of S), we get
J(S_i, x) = (exp(-w_i . x + b_i) / (1 + exp(-w_i . x + b_i))**2) * w_i # remember this is a vector because w_i is a vector
Теперь возьмите повсеместный пример отладки 1.
w_i = b = x = [1, 1]
#define a to make this less cluttered
a = exp(-w_i . x + b) = exp(-3)
J(S_i, x) = a / (1 + a)^2 * [1, 1]
J(S, x) = a / (1 + a)^2 * [[1, 1], [1, 1]]
J(L, S(x)) = [1, 1] #Doesn't depend on S(x)
J(F, x) = J(L, S(x)) . J(S, x) = (a / (1 + a)**2) * [1, 1] . [[1, 1], [1, 1]]
J(F, x) = (a / (1 + a)**2) * [2, 2] = (2 * a / (1 + a)**2) * [1, 1]
J(F, x) = [0.0903533, 0.0903533]
Надеюсь, это поможет вам немного реорганизовать свой код. Вы не можете оценить производные здесь только со значением w_i . x, тебе понадобится w_i а также x отдельно, чтобы правильно рассчитать все.
РЕДАКТИРОВАТЬ
Поскольку мне это интересно, вот мой скрипт на python для вычисления значения и первой производной нейронной сети:
import numpy as np
class Layer:
def __init__(self, weights_matrix, bias_vector, sigmoid_activation = True):
self.weights_matrix = weights_matrix
self.bias_vector = bias_vector
self.sigmoid_activation = sigmoid_activation
def compute_value(self, x_vector):
result = np.add(np.dot(self.weights_matrix, x_vector), self.bias_vector)
if self.sigmoid_activation:
result = np.exp(-result)
result = 1 / (1 + result)
return result
def compute_value_and_derivative(self, x_vector):
if not self.sigmoid_activation:
return (self.compute_value(x_vector), self.weights_matrix)
temp = np.add(np.dot(self.weights_matrix, x_vector), self.bias_vector)
temp = np.exp(-temp)
value = 1.0 / (1 + temp)
temp = temp / (1 + temp)**2
#pre-multiplying by a diagonal matrix multiplies each row by
#the corresponding diagonal element
#(1st row with 1st value, 2nd row with 2nd value, etc...)
jacobian = np.dot(np.diag(temp), self.weights_matrix)
return (value, jacobian)
class Network:
def __init__(self, layers):
self.layers = layers
def compute_value(self, x_vector):
for l in self.layers:
x_vector = l.compute_value(x_vector)
return x_vector
def compute_value_and_derivative(self, x_vector):
x_vector, jacobian = self.layers[0].compute_value_and_derivative(x_vector)
for l in self.layers[1:]:
x_vector, j = l.compute_value_and_derivative(x_vector)
jacobian = np.dot(j, jacobian)
return x_vector, jacobian
#first weights
l1w = np.array([[1,1],[1,1]])
l1b = np.array([1,1])
l2w = np.array([[1,1],[1,1]])
l2b = np.array([1,1])
l3w = np.array([1, 1])
l3b = np.array([0])
nn = Network([Layer(l1w, l1b),
Layer(l2w, l2b),
Layer(l3w, l3b, False)])
r = nn.compute_value_and_derivative(np.array([1,1]))
print r