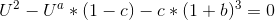Численный поиск корней через Ньютон

Question

Я хочу найти корень (то есть значение x, так что f(x)=0) для функции "func", используя метод Ньютона, импортированный из scipy.optimize. Я написал следующий код:

import numpy

from scipy import optimize


def A(b, c, e=70):
    d = 1 - c
    b_prime = ((1 + b) ** 3)
    wurzel = numpy.sqrt(c * b_prime + d)

    return e * wurzel

def U(b, c, e=70):
    return A(b, c, e=70)/e

def func(U, c, b, a):
    return U(b, c, e=70)**2 - (U(b, c, e=70)**a * (1-c)) - (c * (1+b)**3)

def func_prime(U, c, a):
    return 2*U(b, c, e=70) - (a*(U(b, c, e=70)**(a-1)))*(1-c)

def U_0(b, c):
    numpy.sqrt((c * (1+b)**3) + 1 - c )

res = optimize.newton(func(U, c, b, a), U_0(b, c), fprime=func_prime(U, c, a), args=(c, b, a))

Я вычислил U_0 аналитически, приняв a=0 в func и решив для U. Я получаю следующую ошибку:

Traceback (most recent call last):
  File "root_finding_stack.py", line 25, in <module>
    res = optimize.newton(func(U, c, b, a), U_0(b, c), fprime=func_prime(U, c, a), args=(c, b, a))
NameError: name 'c' is not defined

Ошибка говорит о том, что с не определено, но в этом суть, я не хочу определять a,b и c, но нахожу U(a,b,c) для корня моей функции. Я использую неправильный метод или что я делаю здесь неправильно? Также я не уверен, правильно ли я передал 3 аргумента в функции optimize.newton

Редактировать: я добавил функцию в математической записи

Я пытаюсь найти U(b,c), который заполняет это уравнение

Answer 1

func это функция, чтобы решить. Но вы определили функцию, которая в качестве первого аргумента имеет другую функцию U которая является функцией A, b, c (а также e но это постоянно) и A это также функция.

Ньютон-Рафсон является одномерным решателем и поэтому может найти только корни f(x) не f(g(b,c),a,b,c) где a, b, c все неизвестно.

Также кажется, что вы связываете определения и использование функций Python с определением и использованием математических функций.