Расширение максимального соответствия двудольного графа

Question

Предположим, что есть два таких графика:

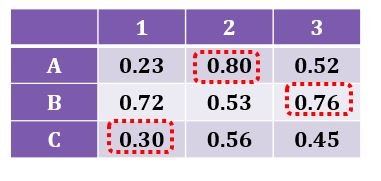
Мы стремимся найти совпадающие соответствия между двумя графами. И теперь мы используем метод, чтобы вычислить сходство двух узлов между двумя графами. w(A,1) означает сходство узла A с левого графа между узлом 1 с правого графа. Тогда у нас может быть такая таблица:

Наша цель состоит в том, чтобы вычислить максимальное соответствие веса всех этих узлов. И мы можем использовать алгоритм Kuhn－Munkras для решения этой проблемы.

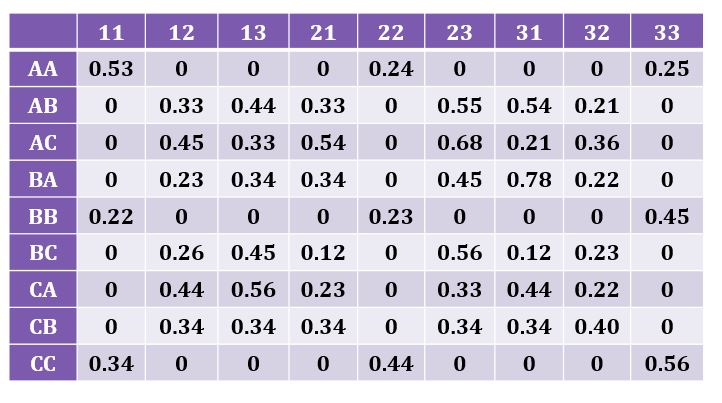
Но теперь вопрос в том, что если мы добавим сходство между ребрами из двух графиков, как мы можем вычислить соответствие максимального веса. Это означает, что таблица становится такой:

AA означает узел A, а AB означает ребро от A до B. Ограничения заключаются в том, что если конечный результат состоит в том, что узел A соответствует узлу 1, ребро AB должно совпадать с 12 или 13. Так что мы можем использовать алгоритм, такой как Kuhn－ Мункрас, чтобы решить эту проблему? Если нет, то как мы можем найти максимальное совпадение веса за полиномиальное время?

Answer 1

Предположим, мы хотим знать, являются ли два графа изоморфными, например, два в вашем примере.

В первом графе у нас есть ребра AC и CB, а во втором - ребра 13 и 32.

Мы можем установить весовую матрицу так, чтобы было высокое вознаграждение за сопоставление любого ребра в первом ребру во втором.

то есть AC->13 и AC->32 и CB->13 и CB->32 будут иметь вес 1, в то время как все другие соответствия имеют нулевой вес.

Между графами существует изоморфизм тогда и только тогда, когда максимальный вес совпадает с весом, равным количеству ребер.

Поэтому ваша задача, по крайней мере, так же сложна, как и изоморфизм графов, поэтому маловероятно, что алгоритм Куна может быть эффективно расширен до этого случая.